Quadratic Equations: Definition, Calculator, Questions, Formula, Examples

What is a Quadratic Equation

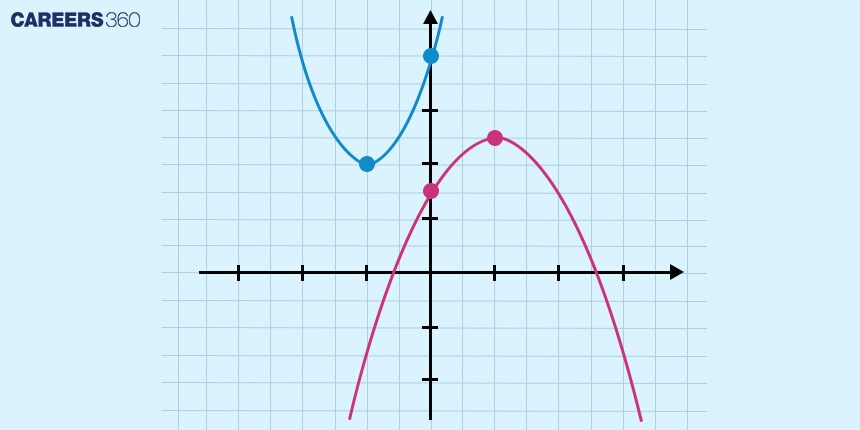
A quadratic equation is a type of polynomial equation of degree two, meaning the variable can have a maximum power of 2. The graph of a quadratic equation is a parabola, which can open either upwards or downwards depending on the coefficients.

The standard form of a Quadratic Equation

The standard form of a quadratic equation is $ax^2+bx+c=0$, where $a,b,c$ are constants and $a \neq 0$.

Here, we can say $a$ is the co-efficient of $x^2$, $b$ is the co-efficient of $x$, and $c$ is the constant term of the quadratic equation.

Roots of a Quadratic Equation

The roots of a quadratic equation, also known as the solutions of a quadratic equation, are the values of the variable that make the equation equal to zero. In other words, when these values are substituted into the quadratic equation, the left-hand side becomes zero. Understanding the nature of roots is a key concept in algebra, Class 10 and Class 12 mathematics, and competitive exam preparation.

What Are the Roots of a Quadratic Equation?

A quadratic equation is generally written in the standard form:

$ax^2 + bx + c = 0$, where $a \neq 0$

The values of $x$ that satisfy this equation are called its roots or solutions. These roots represent the points where the quadratic expression intersects the x-axis when plotted on a graph.

Nature of Roots of a Quadratic Equation

A quadratic equation can have a maximum of two roots. Depending on the values of the coefficients, these roots can be real or complex (imaginary) in nature.

Real Roots of a Quadratic Equation

• Real roots are solutions that exist on the real number line.

• A quadratic equation may have two distinct real roots or two equal real roots.

• These roots are commonly encountered in exam-based quadratic problems.

Complex Roots of a Quadratic Equation

• Complex roots occur when the solutions involve imaginary numbers.

• These roots appear in conjugate pairs.

• Complex roots are especially important in higher algebra and advanced mathematics.

Maximum Number of Roots in a Quadratic Equation

Since the highest power of the variable in a quadratic equation is 2, it can have at most two roots. These roots may be:

• Two distinct real roots

• Two equal real roots

• Two complex (non-real) roots

This classification helps students quickly identify the type of solutions before solving the equation.

Methods of Solving a Quadratic Equation

There are multiple methods of solving a quadratic equation, and the choice of method often depends on the form of the equation. In school exams and competitive exams, students are expected to be comfortable with all standard approaches, including splitting the middle term, completing the square, and the quadratic formula. Below, we explain these important methods step by step with clear examples.

What Is the Middle Term Split Method?

The splitting the middle term method is one of the most commonly used techniques to solve factorable quadratic equations. In this method, the middle term of the quadratic equation is expressed as the sum of two terms such that:

• Their sum equals the coefficient of $x$

• Their product equals the product of the coefficient of $x^2$ and the constant term

This method is especially useful for MCQs and quick problem-solving.

Example: Solve using Middle Term Splitting

Solve $x^2 + 5x + 6 = 0$ using the middle term split method.

Solution:

$x^2 + 5x + 6 = 0$

$⇒ x^2 + (3 + 2)x + 6 = 0$

$⇒ x^2 + 3x + 2x + 6 = 0$

$⇒ x(x + 3) + 2(x + 3) = 0$

$⇒ (x + 3)(x + 2) = 0$

$⇒ x + 3 = 0$ or $x + 2 = 0$

$⇒ x = -3$ or $x = -2$

Hence, the solutions of $x^2 + 5x + 6 = 0$ are –3 and –2.

What Is the Completing the Square Method?

The completing the square method involves rewriting a quadratic equation into a perfect square form, which makes it easier to find the roots. This method is particularly helpful when:

• The equation is not easily factorable

• You want to understand the graphical form of a quadratic equation

• You are preparing for conceptual and descriptive questions

The goal is to transform the equation into the form $(x + p)^2 = q$.

Example: Solve using Completing the Square

Solve $x^2 + 10x - 11 = 0$ using the completing the square method.

Solution:

$x^2 + 10x - 11 = 0$

$⇒ x^2 + 10x + 25 - 36 = 0$

$⇒ x^2 + 2 × x × 5 + 5^2 - 36 = 0$

$⇒ (x + 5)^2 - 6^2 = 0$

$⇒ (x + 5 + 6)(x + 5 - 6) = 0$

$⇒ (x + 11)(x - 1) = 0$

$⇒ x = -11$ or $x = 1$

Hence, the solutions of $x^2 + 10x - 11 = 0$ are –11 and 1.

Mastering these methods of solving quadratic equations helps you tackle a wide variety of exam-level problems, improve algebraic clarity, and choose the fastest and most efficient method based on the question type.

Quadratic Formula (Universal Method to Solve Quadratic Equations)

The quadratic formula is the most reliable and universally applicable method for finding the roots of a quadratic equation. Unlike factorisation-based methods, this approach works for all quadratic equations, whether they are factorable or non-factorable. Because of its accuracy and consistency, the quadratic formula is widely used in school mathematics, board exams, and competitive exams like CAT, XAT, CUET, SSC, and Banking exams.

Quadratic Formula for Solving Quadratic Equations

Any quadratic equation written in the standard form:

$ax^2 + bx + c = 0$, where $a \neq 0$

can be solved using the quadratic formula:

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Where:

• $a$ is the coefficient of $x^2$

• $b$ is the coefficient of $x$

• $c$ is the constant term

This formula directly gives the roots (solutions) of the quadratic equation in a single step.

Example: Solving a Quadratic Equation Using the Quadratic Formula

Solve $x^2 - 10x + 9 = 0$ using the quadratic formula.

Solution:

Comparing $x^2 - 10x + 9 = 0$ with $ax^2 + bx + c = 0$, we get:
$a = 1$, $b = -10$, $c = 9$

Substitute these values into the quadratic formula:

$x = \frac{-(-10) \pm \sqrt{(-10)^2 - 4 × 1 × 9}}{2 × 1}$

$⇒ x = \frac{10 \pm \sqrt{100 - 36}}{2}$

$⇒ x = \frac{10 \pm \sqrt{64}}{2}$

$⇒ x = \frac{10 \pm 8}{2}$

$⇒ x = \frac{10 + 8}{2}$ or $x = \frac{10 - 8}{2}$

$⇒ x = 9$ or $x = 1$

Hence, the solutions of $x^2 - 10x + 9 = 0$ are 9 and 1.

Nature of Roots of a Quadratic Equation

The nature of roots of a quadratic equation refers to the type and characteristics of its solutions, which depend entirely on the value of the discriminant. By analyzing the discriminant, we can determine whether the roots are real or complex, and whether they are distinct or equal, without actually solving the quadratic equation. This concept is extremely important in algebra, Class 10 and 12 mathematics, and competitive exam problems.

Understanding the nature of roots also helps in visualizing the graph of a quadratic equation—specifically, how the parabola intersects or does not intersect the x-axis.

Concept of Discriminant in Quadratic Equations

The discriminant is a mathematical expression derived from the coefficients of a quadratic equation. For a standard quadratic equation:

$ax^2 + bx + c = 0$

the discriminant, denoted by D, is given by:

$D = b^2 - 4ac$

The value of the discriminant plays a crucial role in determining the nature of the roots of the quadratic equation.

Types of Roots Based on the Discriminant

A quadratic equation can have three possible types of roots, depending on the value of the discriminant.

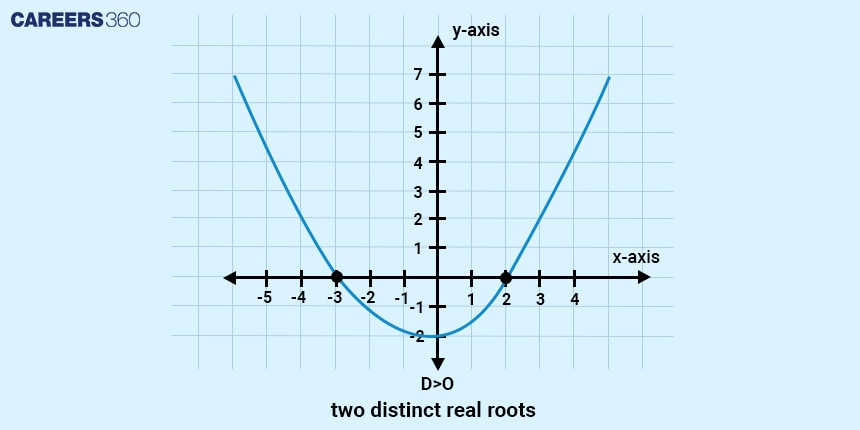
Condition for Distinct Real Roots

When the value of the discriminant is greater than zero:

$D > 0$

the quadratic equation has two distinct and real roots.

This means:

• The equation has two different real solutions

• The graph of the quadratic equation intersects the x-axis at two distinct points

• Such questions are very common in exam-based discriminant problems

This condition helps quickly identify the nature of roots without performing lengthy calculations.

Condition of two equal real roots:

The condition for a quadratic equation to have two equal real roots is when the value of the discriminant equals zero ($D=0$). This means that the quadratic equation has a perfect square trinomial form, resulting in a single repeated solution. Graphically, the parabola representing the equation touches the x-axis at exactly one point.

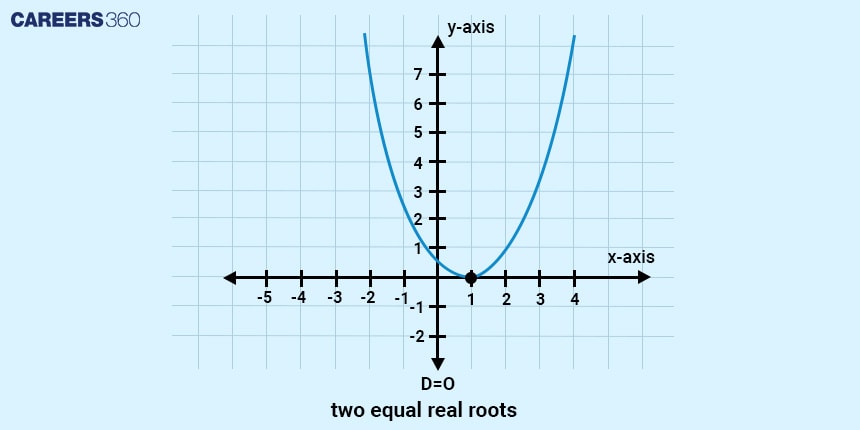
Condition of non-real roots

The condition of non-real roots for a quadratic equation occurs when the value of the discriminant is less than zero ($D<0$) i.e. the discriminant is negative. In such cases, the solutions to the quadratic equation are complex numbers. Geometrically, this means the parabola described by the equation does not touch the x-axis.

Relation between roots and coefficients of a quadratic equation

The relationship between the roots and coefficients of a quadratic equation reveals insightful information about the quadratic equation. These relationships include how the sum and product of the roots can be directly related to the coefficients of the equation.

Sum of roots

If $\alpha$ and $\beta$ are the two roots of a quadratic equation $ax^2+bx+c=0$, then the sum of the roots is given by the formula: $\alpha + \beta = \frac{-b}{a}$, where $a$ is the co-efficient of $x^2$, $b$ is the co-efficient of $x$ of the quadratic equation.

Illustration:

For equation $2x^2-6x+ 1= 0$

The sum of the roots = $\frac{6}{2}=3$

Product of roots

If $\alpha$ and $\beta$ are the two roots of a quadratic equation $ax^2+bx+c=0$, then the product of the roots is given by the formula: $\alpha \beta = \frac{c}{a}$, where $a$ is the co-efficient of $x^2$, $c$ is the constant term of the quadratic equation.

Illustration:

For equation $2x^2-6x+ 1= 0$

Product of the roots = $\frac{1}{2}$

Formation of Quadratic Equation using the sum of the roots and the product of the roots:

If S is the sum of the roots and P is the product of the roots. Then, the quadratic equation is given by
$x^2-Sx+P=0$

Illustration:

If the sum of the roots of a quadratic equation is $\frac{3}{2}$ and the product of roots is $\frac{1}{4}$, Then the quadratic equation is given by

$x^2-\frac{3}{2}x+ \frac{1}{4}= 0$

I.e. $4x^2-6x+ 1= 0$

Word Problems on Quadratic Equations

Word problems on quadratic equations can be of several types as given below:

• Problems related to speed, time, and distance.

• Problems on boats and streams

• Problems on ages

• Problems involving the formation of quadratic equations to find the unknown

Example: The ratio of the father's age to his son's age is 5 : 3. The product of the numbers representing their ages is 960. The ratio of their ages after 6 years will be:

Solution:

The ratio of the ages of father to his son = 5 : 3

Let the age of the father = $5x$

The age of the son = $3x$

Product of their ages = 960

⇒ $(5x)(3x) = 960$

⇒ $15x^2 = 960$

⇒ $x^2 = 64$

⇒ $x = 8$ (since age can not be negative)

So, the age of father = $5x$ = 5 × 8 = 40 years

⇒ The age of son = $3x$ = 3 × 8 = 24 years

The age of father and son after 6 years will be

⇒ Father's age = 40 + 6 = 46 years

⇒ Son's age = 24 + 6 = 30 years

⇒ The ratio of the ages of father to son = Father's age : Son's age = 46 : 30 = 23 : 15

Hence, the correct answer is $23:15$.

Tips and Tricks

• Always simplify the quadratic equation to the standard form before solving.

• Check the discriminant to understand the nature of the roots before solving.

• Practice different methods to find the one that works best for you.

• Use the quadratic formula when the equation is not easily factorable.

Practice Questions/Solved Examples

Q.1. What is the value of $x$ in the equation $\sqrt{\frac{1+x}{x}}-\sqrt{\frac{x}{1+x}}=\frac{1}{\sqrt6}$?

1. –2

2. 3

3. 2

4. None of these

Hint: Square both sides of the given equation and frame a quadratic equation to find its roots.

Solution:

Given: $\sqrt{\frac{1+x}{x}}-\sqrt{\frac{x}{1+x}}=\frac{1}{\sqrt6}$

Squaring both sides

⇒ $\left(\sqrt{\frac{1+x}{x}}-\sqrt{\frac{x}{1+x}}\right)^{2}=\left(\frac{1}{\sqrt6}\right)^{2}$

⇒ $\frac{1+x}{x} +\frac{x}{1+x}-2=\frac{1}{6}$

⇒ $\frac{1+x}{x} +\frac{x}{1+x}=\frac{13}{6}$

⇒ $\frac{1+x^{2}+2x+x^{2}}{x+x^{2}}=\frac{13}{6}$

⇒ $6+6x^{2}+12x+6x^{2}=13x+13x^{2}$

⇒ $6+12x^{2}+12x=13x+13x^{2}$

⇒ $x^{2}+x-6=0$

⇒ $x^{2}+3x-2x-6=0$

⇒ $x(x+3)-2(x+3)=0$

⇒ $(x+3)(x-2)=0$

⇒ $x=-3, 2$

From the given options we can say that the value of $x$ is 2.

Hence, the correct answer is option (3).

Q.2. The sum of twice a number and thrice its reciprocal is $\frac{25}{2}$. What is the number?

1. 7

2. 6

3. 5

4. 4

Hint: Let the number be $x$. Then use the given information to make a quadratic equation.

Solution:

Given: The sum of a twice a number and thrice its reciprocal is $\frac{25}{2}$.

Let the number be $x$.

According to the question,

$2x+\frac{3}{x}=\frac{25}{2}$

$\Rightarrow 4x^2+6=25x$

$\Rightarrow 4x^2-25x+6=0$

$\Rightarrow 4x^2-24x-x+6=0$

$\Rightarrow (4x-1)(x-6)=0$

$\Rightarrow (4x-1)=0$ or $(x-6)=0$

$\Rightarrow x=6$ or $\frac{1}{4}$

After checking the options, we get, $x=6$

Hence, the correct answer is option (2).

Q.3. If the sum of a non-zero number and thrice its reciprocal is $\frac{52}{7}$. Find the number.

1. 8

2. 9

3. 7

4. 6

Hint: Let the number be $x$. Then use the given information to make a quadratic equation.

Solution:

Given: The sum of a non-zero number and thrice its reciprocal is $\frac{52}{7}$.

Let the number be $x$.

According to the question,

$x+\frac{3}{x}=\frac{52}{7}$

$\Rightarrow 7x^2-52x+21=0$

$\Rightarrow (7x-3)(x-7)=0$

$\Rightarrow (7x-3)$ or $(x-7)=0$

$\Rightarrow x=7$ or $ \frac{3}{7}$

After checking the options, we get, $x=7$

Hence, the correct answer is option (3).

Q.4. If $(x-2)(x-p) = x^2-ax+6$, then the value of $(a - p)$ is:

1. 0

2. 1

3. 2

4. 3

Hint: Expand the brackets and compare both sides of the equation.

Solution:

Given: $(x-2)(x-p) = x^2-ax+6$

⇒ $x^2-px-2x+2p=x^2-ax+6$

⇒ $x^2-(p+2)x+2p=x^2-ax+6$

By comparing both sides of the equation,

$p+2=a$

⇒ $a-p=2$

Hence, the correct answer is option (3).

Q.5. If $x^{2}+y^{2}+2x+1=0$, then the value of $x^{31}+y^{35}$ is:

1. –1

2. 0

3. 1

4. 2

Hint: The addition of two positive squares is zero only if the numbers are zero individually. Use this information to solve the question.

Solution:

Given:

$x^{2}+y^{2}+2x+1=0$

⇒ $x^{2}+2x+1+y^{2}=0$

⇒ $(x+1)^2+y^2=0$

Since the addition of the squares of the two terms is zero,

So, both the terms are individually zero.

Therefore, $(x+1)^2=0$ and $y^2=0$.

⇒ $x=-1$ and $y=0$

Now, $x^{31}+y^{35}$

= $(-1)^{31}+(0)^{35}$

= –1

Hence, the correct answer is option (1).

Q.6. If the sum of the roots of a quadratic equation is 1 and the product of the roots is –20, find the quadratic equation.

1. $x^{2}–x–20=0$

2. $x^{2}+x+20=0$

3. $x^{2}+x–20=0$

4. $x^{2}–x+20=0$

Hint: By using the concept of a quadratic equation: $x^{2} – (\text{sum of the root})x+(\text{product of the root})=0$ finding the desired equation.

Solution:

Given: The sum of the roots = 1

The product of the roots is = –20

We know that quadratic equation: $x^{2}–(\text{sum of the root})x+(\text{product of the root})=0$

⇒ $x^{2}–(1)x+(–20)=0$

⇒ $x^{2}–x–20=0$

Hence, the correct answer is option (1).

Q.7. What is the difference between the cube and square of the common root of $x^2-8x+15=0$ and $y^2+2y-35=0$

1. 76

2. 100

3. 294

4. 318

Hint: Find the roots of both equations to get the common root using factorisation.

Solution:

Here,

$x^2-8x+15=0$

⇒ $(x-5)(x-3)=0$

So, $x=5,3$

$y^2+2y-35=0$

⇒ $(y-5)(y+7)=0$

So, $y=5,-7$

Here, the common root is 5.

So, the difference between the cube and square of 5 $=(5^3-5^2)=125-25=100$

Hence, the correct answer is option (2).

Q.8.

If $2\left [x^{2} +\frac{1}{x^{2}}\right]-2\left [x-\frac{1}{x} \right]-8=0$, what are the two values of $\left (x-\frac{1}{x} \right)\;$?

1. –1 or 2

2. 1 or –2

3. –1 or –2

4. 1 or 2

Hint: Use the formula, $a^2+b^2=(a-b)^2+2ab$, and factorisation by splitting the middle term.

Solution:

Given: $2\left [x^{2} +\frac{1}{x^{2}} \right]-2\left [ x-\frac{1}{x} \right]-8=0$

$⇒2\left [(x -\frac{1}{x})^{2}+2 \right]-2\left [ x-\frac{1}{x} \right ]-8=0$

Let $(x -\frac{1}{x})=t$

The equation becomes $2(t^{2}+2)-2t-8=0$

$⇒2t^{2}-2t-4=0$

$⇒t^{2}-2t+t-1=0$

$⇒(t-2)(t+1)=0$

$⇒t=-1,2$

So, $(x -\frac{1}{x})=-1,2$

Hence, the correct answer is option (1).

Q.9. If $x-\frac{1}{x}=1$, then what is the value of $\left (\frac{1}{x-1}-\frac{1}{x+1}+\frac{1}{x^{2}+1}-\frac{1}{x^{2}-1} \right)\;$?

1. $\pm \sqrt{5}$

2. $\frac{2}{5}$

3. $\pm\frac{2}{\sqrt{5}}$

4. $\pm\frac{\sqrt{5}}{2}$

Hint: Given: $x-\frac{1}{x}=1$ or, $x^{2}-1=x$ or, $x^{2}+1=x+2$

Substitute, $x^{2}-1=x$ and $x^{2}+1=x+2$

Solution:

Given: $x-\frac{1}{x}=1$

$⇒x^{2}-1=x$

$⇒x^{2}+1=x+2$

$\left (\frac{1}{x-1}-\frac{1}{x+1}+\frac{1}{x^{2}+1}-\frac{1}{x^{2}-1} \right)$

$=(\frac{2}{x^{2}-1}+\frac{1}{x^{2}+1}-\frac{1}{x^{2}-1})$

$=(\frac{1}{x^{2}-1}+\frac{1}{x^{2}+1})$

$=(\frac{2x^{2}}{(x^{2}-1)(x^{2}+1)})$

Using $x^{2}-1=x$ and $x^{2}+1=x+2$, we get,

$=(\frac{2x^{2}}{(x)(x+2)})$

$=\frac{2x}{x+2}$

Solving $x^{2}-x-1=0$, we get $x=\frac{1\pm\sqrt{5}}{2}$

So, $x+2=\frac{5\pm\sqrt{5}}{2}$

When $x=\frac{1+\sqrt{5}}{2}$, $\frac{2x}{x+2}=\frac{2}{\sqrt{5}}$

When $x=\frac{1-\sqrt{5}}{2}$, $\frac{2x}{x+2}=-\frac{2}{\sqrt{5}}$

Hence, the correct answer is option (3).

Q.10. If $\sqrt{x}=\sqrt{3}-\sqrt{5}$, then the value of $x^2-16x+6$ is:

1. $0$

2. $-2$

3. $2$

4. $4$

Hint: Square both sides of the equation twice to get the result.

Solution:

Given: $\sqrt{x}=\sqrt{3}-\sqrt{5}$

By squaring both the sides, we get,

$x=3+5-2\sqrt{15}$

⇒ $x-8=-2\sqrt{15}$

Again, squaring both the sides, we get,

$x^2-16x+64=60$

⇒ $x^2-16x+4=0$

$\therefore x^2-16x+6=2$

Hence, the correct answer is option (3).