Introduction to Quadrilaterals: Definition, Formula, Examples
Introduction to quadrilaterals is an important chapter of geometry and indeed Mathematics. Quadrilaterals have four sides and their opposite angles may or may not be equal based on their properties. They are one type of polygon. In this article, we are going to discuss about some types of quadrilaterals like squares, rectangles, rhombus etc. Students can also practice the introduction to quadrilaterals worksheet to capatalise their concepts.
This Story also Contains
- Quadrilateral: A general description
- Types of Quadrilateral
- Perimeter of a quadrilateral
- Area of Quadrilaterals
- Important points
- Practice Questions/Solved Examples
We will also cover “Introduction to Quadrilaterals activity”, “Checking Intro to Quadrilaterals video”, “Introduction to Quadrilaterals 3rd grade”, and “Introduction to Quadrilaterals Class 8” in this article.
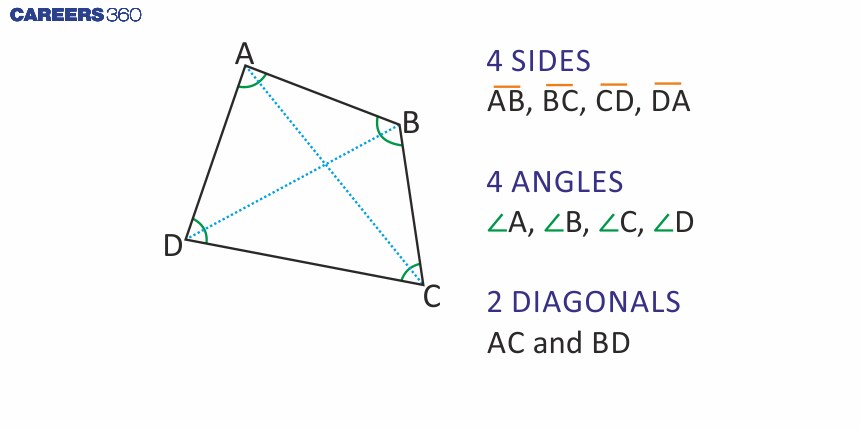
Quadrilateral: A general description
Quadrilaterals are important part of geometry having four sides. There are some important quadrilaterals i.e. squares, rectangles, trapezium, rhombus, and parallelograms. A quadrilateral also has four angles, four vertices, 12 edges, and two diagonals.
There are several formulas in geometry to calculate the area and parameters of the quadrilaterals.
| Quadrilateral | Two-dimensional plane figure enclosed by 4 line segments Or A polygon with 4 edges and 4 vertices |
| Number of Sides | 4 |
| Number of Vertices | 4 |
| Number of Diagonals | 2 |
| Sum of all interior angles | 360 degrees |
| Sum of all exterior angles | 360 degrees |
Real-life examples of quadrilateral
Quadrilaterals are ubiquitous in daily life. Some examples include:
Tables and Desks: Often rectangular or square.
Books and Notebooks: Typically rectangular.
Computer Screens: Usually rectangular.
Playing Fields: The football and basketball courts are rectangular.
Windows and Doors: Commonly rectangular.
Types of Quadrilateral
S. no. | Name of Quadrilateral | General description | Diagram |
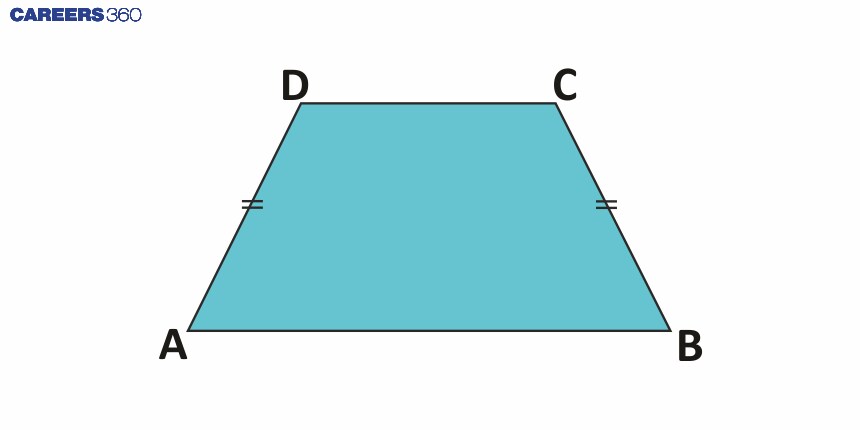
1 | Trapezium | A trapezium is a type of quadrilateral that has at-least one pair of parallel sides. |
|
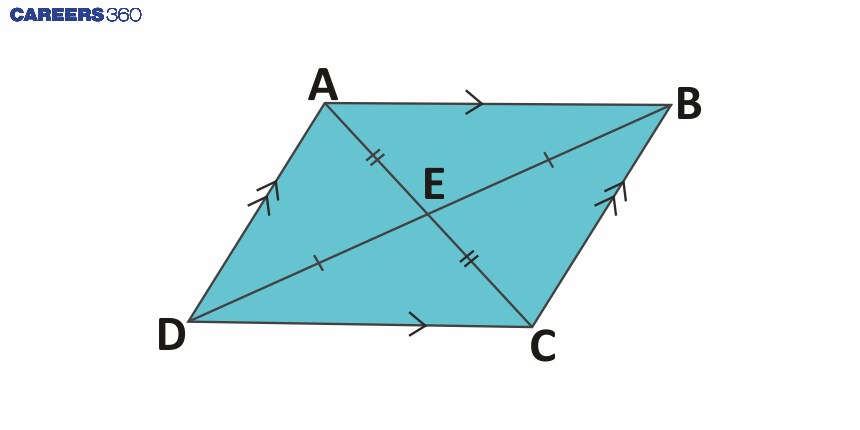
2 | Parallelogram | A parallelogram is a type of quadrilateral where opposite sides are both equal in length and parallel to each other. |
|
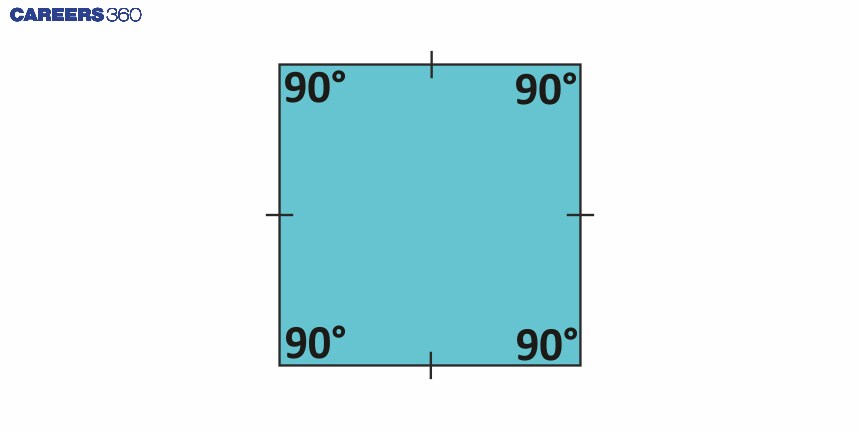
3 | Square | A square is a quadrilateral with four equal sides and four right angles, each measuring 90 degrees. |
|
4 | Rectangle | A rectangle is a quadrilateral with opposite sides that are equal in length and all four interior angles that are right angles (90 degrees). |
|
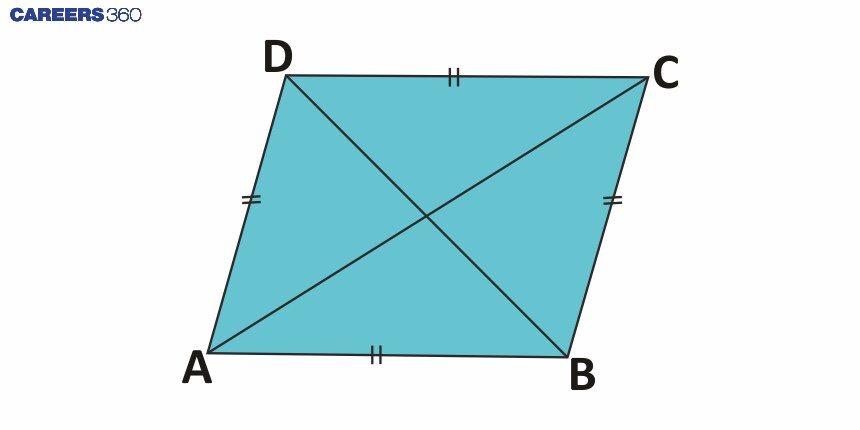
5 | Rhombus | A rhombus is a type of quadrilateral with all four sides of equal length. |
|
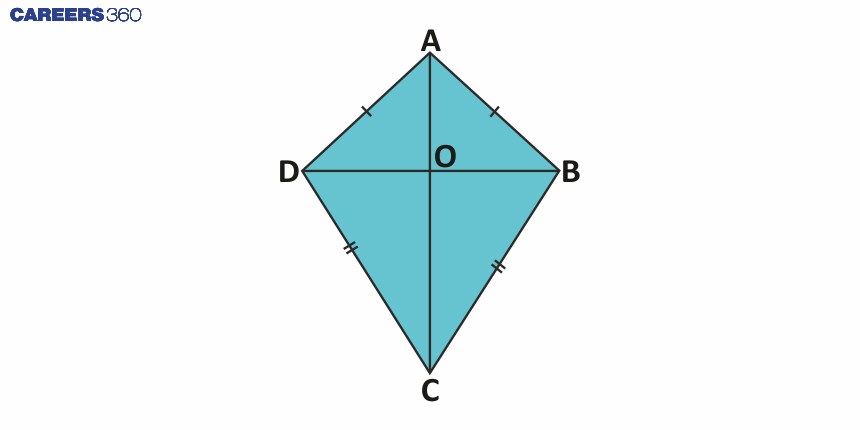
6 | Kite | A kite is a quadrilateral with two distinct pairs of adjacent sides that are equal in length. |
|
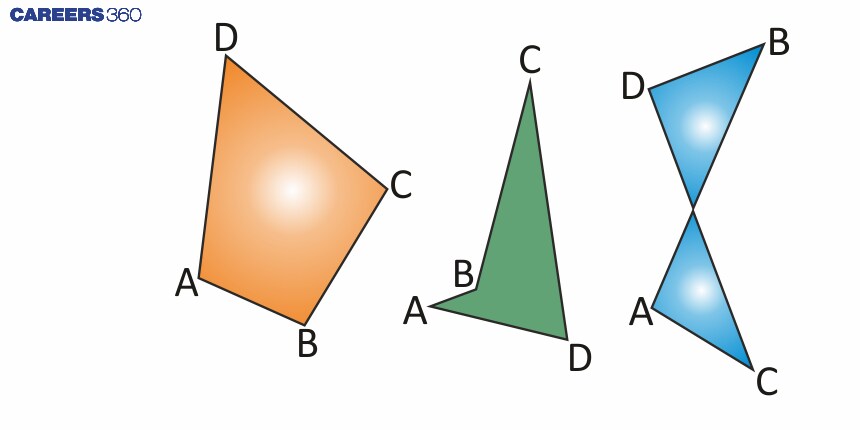
Convex, Concave and Intersecting Quadrilaterals
Convex Quadrilaterals: A polygon of four sides in which all interior angles are measured less than 180 degrees, and no sides are inwardly curved. This polygon is considered as Convex Quadrilateral. In a convex quadrilateral, any line segment drawn between two points inside the shape will lie entirely within the shape. Examples include squares, rectangles, and parallelograms.
Concave Quadrilaterals: A concave quadrilateral has at least one interior angle greater than 180 degrees, and at least one vertex "caves in" towards the interior of the shape. This results in at least one diagonal lying outside the quadrilateral. An example of a concave quadrilateral is an arrowhead shape or a dart.
Intersecting Quadrilaterals: An intersecting quadrilateral, also known as a self-intersecting or crossed quadrilateral, is a four-sided polygon where two sides cross over each other. This results in a shape that is not simple. A common example of an intersecting quadrilateral is the bowtie or butterfly shape, also called a complex quadrilateral.
Perimeter of a quadrilateral
Quadrilateral Name | Perimeter |
Square | 4 × Side |
Rectangle | 2 × (Length + Breadth) |
Parallelogram | 2 × (Base + Side) |
Rhombus | 4 × Side |
Kite | 2 × (Sum of the unequal adjacent pairs) |
Area of Quadrilaterals
Quadrilateral Name | Area |
Area of a Parallelogram | Base × Height |
Area of a Rectangle | Length × Breadth |
Area of a Square | Side × Side |
Area of a Rhombus | $\frac{1}{2}$ × Diagonal$_1$ × Diagonal$_2$ |
Area of a Kite | $\frac{1}{2}$ × Diagonal$_1$ × Diagonal$_2$ |
Important points
The sum of the all interior angles of a quadrilateral is 360 degrees.
Different kinds of quadrilaterals exhibits distinct properties that make them different from each other and help in their identification and calculation of their perimeter and area.
Understanding of Quadrilaterals makes one to work effectively in various fields.
Practice Questions/Solved Examples
Q.1.
A man walking at 3 km/hr crosses a square field diagonally in 2 minutes. The area of the field (in square metres) is:
3000
5000
6000
2500
Hint: Use this formula:
Area of the square field $=\frac{1}{2}×(\text{diagonal})^2$
Solution:
A man walking at the speed of 3 km/hr = $3×\frac{5}{18}=\frac{5}{6}$ m/s
The distance covered in 2 min $ = \frac{5}{6}×2×60=100$ m
$\therefore$ Length of the diagonal = 100 m
$\therefore$ Area of the field $ = \frac{1}{2}×(\text{diagonal})^2=\frac{1}{2}×(100)^2 = 5000$ square metres
Hence, the correct answer is option (2).
Q.2.
The ratio of the length to width of a certain rectangle is $3:2$ and the area is 150 cm2. The perimeter of the rectangle (in cm) is:
20
30
50
40
Hint: Area of the rectangle = Length $\times$ Breadth
Perimeter of a rectangle = 2 × (Length + Breadth)
Solution:
Let the length of the rectangle be $3x$ and the width be $2x$.
Area = length $\times$ width $= 2x \times 3x = 6x^{2}$
Given $6x^{2} = 150$
$⇒x^{2} = 25$
$\therefore x = 5$ cm
Breadth = 5 × 2 = 10 cm
Length = 5 × 3 = 15 cm
$\therefore$ Perimeter of rectangle = 2 × (Length + Breadth) = 2 × (15 + 10) = 50 cm
Hence, the correct answer is option (3).
Q.3.
The measure of three angles of a quadrilateral is in the ratio $1:2:3$. If the sum of these three measures equals the measure of the fourth angle, then find the smallest angle.
$30^\circ$
$40^\circ$
$60^\circ$
$50^\circ$
Hint: The sum of the angles of a quadrilateral is $360^\circ$.
Solution:
Let the 1st, 2nd, and 3rd angles be $x$, $2x$, and $3x$.
$\therefore$ The 4th angle = $x+2x+3x=6x$
We know that the sum of the angles of the quadrilateral is $360^\circ$.
According to the question,
$x+2x+3x+6x=360^\circ$
⇒ $12x=360^\circ$
⇒ $x=30^\circ$
Since, the smallest angle is $x$, so $x=30^\circ$
Hence, the correct answer is option (1).
Q.4.
ABCD is a quadrilateral. The length of the diagonal AC is 24 cm. The sum of the perpendicular drawn from vertex B and D on the diagonal AC is 10 cm. What is the area of the quadrilateral?
240 cm2
180 cm2
120 cm2
90 cm2
Hint: Find the area of the quadrilateral using the formula, $=\frac{1}{2}\times(h_1+h_2)\times d$ where $d$ and $(h_1+h_2)$ are its diagonals and sum of heights.
Solution:
Given: $d=24$ cm and $h_1+h_2=10$ cm.
The area of the quadrilateral $=\frac{1}{2}\times(h_1+h_2)\times d$ where $d$ and $(h_1+h_2)$ are its diagonals and sum of heights.
So, the area $=\frac{1}{2}\times10\times 24=120$ cm2
Hence, the correct answer is option (3).
Q.5.
The lengths of the diagonals of a rhombus are 24 cm and 10 cm, then the perimeter of the rhombus (in cm) is:
52
56
68
78
Hint: Use the formula: The length of the sides of a Rhombus = $\sqrt{(\frac{a}{2})^2+(\frac{b}{2})^2}$, where $a$ and $b$ are the diagonals of the rhombus.
Solution:
Given: The lengths of the diagonals of a rhombus are 24 cm and 10 cm.
So, the length of the sides
= $\sqrt{(\frac{24}{2})^2+(\frac{10}{2})^2}$
= $\sqrt{12^2+5^2}$
= $\sqrt{169}$
= $13$
$\therefore$ The perimeter of the rhombus = (4 × 13) = 52 cm
Hence, the correct answer is option (1).
Q.6.
The perimeter of a Rhombus is 60 cm and one of its diagonal is 24 cm. The area of the Rhombus is:
108 sq. cm
216 sq. cm
432 sq. cm
206 sq. cm
Hint: Use the formula: Area of the Rhombus = $\frac{1}{2}×a×b$, where $a$ and $b$ are diagonals of the Rhombus.
Solution:
Given: The perimeter of a Rhombus is 60 cm and one of its diagonals is 24 cm.
Let $a$ cm and $b$ cm be the two diagonals of the Rhombus.
Then, perimeter = $2\sqrt{a^2+b^2}$
⇒ $60 = 2\sqrt{24^2+b^2}$
⇒ $30 = \sqrt{60^2+b^2}$
⇒ $576+b^2=900$
⇒ $b^2=324$
⇒ $b=18$
Therefore, the area of the Rhombus = $\frac{1}{2}×24×18$ = $216$ sq. cm
Hence, the correct answer is option (2).
Q.7.
How many tiles, each 4 decimetre square, will be required to cover the floor of a room 8 m long and 6 m broad?
200
260
280
300
Hint: Number of tiles required = $\frac{\text{Area of floor}}{\text{Area of 1 tile}}$
Solution:
We have to find how many tiles, each 4 decimetre square, will be required to cover the floor of a room 8 m long and 6 m broad.
Here, the area of the floor = (8 × 6) = 48 m2
Now 48 m2 = (48 × 100) = 4800 dm2
Also, the area of a square tile = (4 × 4) = 16 dm2
Therefore, the required number of tiles = $\frac{4800}{16}=300$
Hence, the correct answer is option (4).
Q.8.
The area of the rhombus is 216 cm2 and the length of its one diagonal is 24 cm. The perimeter (in cm) of the Rhombus is:
52
60
120
100
Hint: The diagonals of a rhombus bisect each other at right angles. The area (A) of a Rhombus = $\frac{1}{2}d_1d_2$, where $d_1,d_2$ are diagonals.
Solution:
Area of Rhombus = 216 cm2
Length of one of the diagonals ($d_1$) = 24 cm
We know, the area ($A$) of a Rhombus = $\frac{1}{2}d_1d_2$
$⇒d_2 = \frac{2A}{d_1}$
$⇒d_2 = \frac{2×216}{24}$
$⇒d_2 = 18$ cm
Also, the diagonals of a Rhombus bisect each other at right angles.
Therefore, each side (s) of the Rhombus is given by:
s = $\sqrt{(\frac{d_1}{2})^2+(\frac{d_2}{2})^2}$
Putting the given values:
$\therefore$ s = $\sqrt{(\frac{24}{2})^2+(\frac{18}{2})^2}$ = 15 cm
$\therefore$ The perimeter, $P = 4×s= 4×15 = 60$ cm
Hence, the correct answer is option (2).
Q.9.
The length and breadth of a rectangular field are in the ratio of $4:3$. If the perimeter of the field is 70 m, then what will be the breadth (in metres)?
12
15
18
24
Hint: Use the following formula to solve the question:
Perimeter of rectangle = 2 × (Length + Breadth)
Solution:
Given: Ratio of length and breadth = 4 : 3
Perimeter = 70 m
Let the length be $4x$ and breadth be $3x$.
Perimeter of rectangle = 2 × (Length + Breadth)
$⇒ 70=$ 2 × (Length + Breadth)
$⇒2×(4x + 3x) = 70$
$⇒7x= 35$
$\therefore x = 5$ m
$\therefore$ Breadth = $3x$ = 3 × 5 = 15 m
Hence, the correct answer is option (2).
Q.10.
A parallelogram has sides 15 cm and 7 cm long. The length of one of the diagonals is 20 cm. The area of the parallelogram is:
42 cm2
60 cm2
84 cm2
96 cm2
Hint: Use the formula: Area of parallelogram = 2 × Area of one of its triangles
And find the area of the triangle by Heron's formula = $\sqrt{s(s-a)(s-b)(s-c)}$ where $s$ is semiperimeter and $a,b,$ and $c$ are three sides of the triangle.
Solution:
Given: A parallelogram has sides 15 cm and 7 cm long. The length of one of the diagonals is 20 cm.
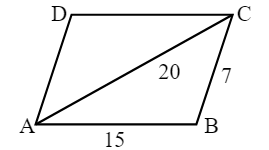
Let ABCD be the parallelogram.
The diagonal of a parallelogram divides it into two equal triangles.
The half perimeter of one of the triangles, $s$ = $\frac{15+7+20}{2}=21$ cm
Area of triangle by heron's formula = $\sqrt{s(s-a)(s-b)(s-c)}$
So, the area of one of the triangles is:
= $\sqrt{21(21-15)(21-7)(21-20)}$
= $\sqrt{21×6×14×1}$
= 42 cm2
So, Area of the parallelogram = 2 × Area of one of its triangles = (2 × 42) cm2 = 84 cm2
Hence, the correct answer is option (3).
Frequently Asked Questions (FAQs)
360 degrees.
No.
Reason: If all angles are acute then sum of all angles becomes less than 360 degree which is not true for a quadrilateral.
In a convex quadrilateral all interior angles are less than 180 degrees, and both diagonals lie inside the quadrilateral.
Whereas in a concave quadrilateral at least one interior angle greater than 180 degrees, and at least one diagonal lie outside the quadrilateral.
Vertices = 4, Sides = 4.
Yes, all rhombuses are parallelograms. A rhombus satisfies the basic definition of a parallelogram such as opposite sides are parallel and diagonals bisect each other.