Ratio and Proportion: Introduction, Formula, Questions, Examples

Introduction to Ratio and Proportion is a fundamental part of mathematics and is often included in educational resources such as an introduction to ratio and proportion PDF or an introduction to ratio and proportion PPT. To discuss and elaborate on this topic, we can use materials like "Intro to ratios and proportions" or guides for "Introducing ratio and proportion" to make the concept clearer.

Understanding the ratio and proportion formula is crucial, as it forms the base for solving various problems. To practice, students can work on ratio and proportion questions or use a ratio and proportion worksheet to enhance their skills.

During the curriculum or syllabus making for younger students like class 6 or lower, "ratio and proportion class 6" is a very common topic. Resources like "Ratio and Proportion Questions for Class 6 PDF" and "Ratio and Proportion Class 6 Questions with Answers" can provide valuable practice and make a strong base of the concepts of Ratio and Proportion.

What is Ratio?

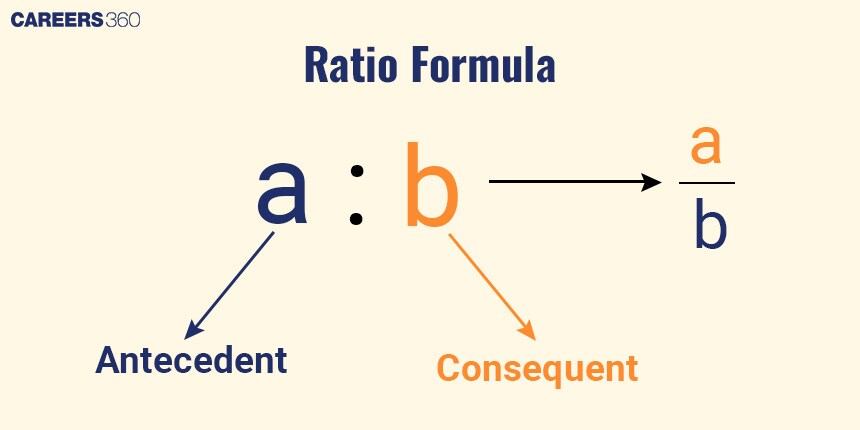
To compare two quantities or check how many times one quantity is contained in another quantity, we use Ratio.

A and B are said to be in ratio if it is written A : B or $\frac{A}{B}$, Where B $\neq 0$

It is read as “A is to B”.

The left side of the ratio is called Antecedent and the right side is called Consequent.

Ratio is denoted by “:”.

Example: Boy : Girl = 1 : 3, which means for every 1 boy, there are 3 girls.

Concept of Proportion and Variation

Two ratios a : b and x : y are said to be proportional to each other if a : b = x : y

It is written as a : b :: x : y.

a and y are called “extreme terms” and b and x are called “mean terms”.

Proportion is denoted by “::”.

Example:

Two numbers $x$ and $y$ are such that their mean proportion is 9 and the third proportion is 243. What are the values of $x$ and $y$?

Sol: Two given numbers are $x$ and $y$.

The mean proportion between $x$ and $y$ is 9.

⇒ $x:9=9:y$

⇒ $\frac{x}{9}=\frac{9}{y}$

$⇒x=\frac{81}{y}$ ------------------------------(1)

The third proportion to $x$ and $y$ is 243.

⇒ $x:y=y:243$

⇒ $\frac{x}{y}=\frac{y}{243}$

By putting the value of $x$, we get,

$⇒y^{2}=243×\frac{81}{y}$

$⇒y^{3}=243×81$

$⇒y^{3}=(27)^{3}$

$\therefore y=27$

Putting this value in equation (1), we get,

$\therefore x=\frac{81}{27}=3$

Hence, the values of $x$ and $y$ are 3 and 27.

How do you use the concept of ratio in partnership?

The concept of ratio is essential in partnerships to ensure the profits are distributed fairly based on their contributions or agreements.

Suppose if A invested 15000 and B invested 20000, then profits will be distributed in the ratio 15000 : 20000 = 3 : 4, which means for every Rs. 3 A gets, B will get Rs. 4.

Sometimes partners withdraw money during the tenure. Then we have to adjust that, then make the ratio to calculate how much profit each gets.

Suppose A invests 15000 and B invests 20000 for 1 year. But B withdraws 50000 from the capital after 6 months.

Here, profits will be distributed in the ratio (15000 × 12) : (20000 × 12 - 50000) = 18 : 19

Same as profits, if partners incur a loss, then it will be also distributed among them based on their contributions or agreements.

Example:

A and B invest in a business in a ratio of 4 : 5. After 10 months, B leaves the business after withdrawing his investment. In the first year, the business made a profit of Rs. 49,000. What is B's share (in Rs.) in this profit?

Sol: A and B invest in a business in a ratio of 4 : 5.

Let the investment of A and B be 4$x$ and 5$x$ respectively.

Profit ratio of A and B = (capital of A × time period of A) : (capital of B × time period of B)

= (4$x$ × 12) : (5$x$ × 10)

= 48 : 50

= 24 : 25

Since the total profit = Rs. 49000,

So, the share of B = $\frac{25}{(24+25)}$ × 49000

= $\frac{25}{49}$ × 49000

= Rs. 25000

Hence, the B’s share is 25,000.

Fraction to Ratio

It is a very straightforward process. A fraction is written as $\frac{a}{b}$, where a is the numerator and b is the denominator. When we convert it into a ratio, the numerator becomes antecedent and is placed on the left of the ratio sign. The denominator becomes the consequent and is placed on the right of the ratio sign.

$\frac{2}{3}$ = 2 : 3

If the terms of the fraction can be simplified, then after converting them into ratios, divide them with the greatest common divisor (GCD) to simplify.

$\frac{4}{6}$ can be simplified into 2 : 3 as GCD is 2.

If there are two or more fractions and we have to convert them into ratios, then find the least common multiple (LCM) of the numerators and multiply the fractions with it to get the ratio.

$\frac{2}{5} : \frac{7}{15} : \frac {17}{30}$

Here, LCM of 5, 15, 30 is 30.

So, $\frac{2}{5} ×30: \frac{7}{15}×30 : \frac {17}{30}×30$

= 12 : 14 : 17

Example:

If $\frac{2}{3}$ of A = 75% of B = 0.6 of C, then $A:B:C$ is:

Sol: Given: $\frac{2}{3}$ of A = 75% of B = 0.6 of C

Here, $\frac{2}{3}$ of A = 75% of B

⇒ $\frac{2A}{3}=\frac{75B}{100}$

⇒ $\frac{A}{B}=\frac{9}{8}$

Let A and B be 9 and 8 respectively.

Now, 75% of B = 0.6 of C

⇒ $\frac{75B}{100}=\frac{6C}{10}$

⇒ $\frac{B}{C} =\frac{4}{5} =\frac{8}{10}$

So, $A:B: C = 9:8:10$

Comparing two or more ratios

Comparing two or more ratios can be done through various methods like cross multiplication, converting in decimal form or finding a common numerator or denominator.

First, convert the ratios into fractions then calculate.

$a : b > c : d$, if $\frac{a}{b}$ > $\frac{c}{d}$

Let’s understand this with an example.

Find which ratio is bigger. 5 : 7, 8 : 9

In fraction form:

$\frac{5}{7}, \frac{8}{9}$

Using cross multiplication, we get, 5 × 8 = 40, 7 × 9 = 63

As 63 > 40, so $\frac{8}{9}$ > $\frac{5}{7}$

We can also use the decimal conversion process.

$\frac{5}{7}$ = 0.714

$\frac{8}{9}$ = 0.888

So, $\frac{8}{9}$ > $\frac{5}{7}$

But for bigger ratios, it is a tough process.

Now, let's use the most common process.

LCM of 7 and 9 is 63.

$\frac{5}{7} × 63$ = 45

$\frac{8}{9} × 63$ = 56

As 56 > 45, so $\frac{8}{9}$ > $\frac{5}{7}$.

Example:

The sum of the three numbers is 540. The ratio of second to third is 9 : 13 and that of first to third is 2 : 7. The third number is:

The ratio of 2nd : 3rd = 9 : 13

And the ratio of 1st : 3rd = 2:7

3rd number is common in both ratios, so to make the value equal, we need to multiply by 7 in 9 : 13 and by 13 in 2 : 7.

We get 1st : 2nd : 3rd = 26 : 63 : 91

Let the 1st, 2nd and 3rd number be 26x, 63x, and 91x.

According to the question,

26x + 63x + 91x = 540

⇒ 180x = 540

$\therefore$ x = 3

Thus, the 3rd number = (91 × 3) = 273

Hence, the correct answer is 273.

Types of Ratios

There are various types of ratios each with its own characteristics and applications.

Here are some main types of ratios listed below.

1. Simple ratio

2. Inverse ratio

3. Continued ratio

4. Equivalent ratio

5. Duplicate ratio

6. Triplicate ratio

7. Sub duplicate ratio

8. Sub triplicate ratio

9. Compounded ratio

Properties of ratios

Ratios have several important properties that are useful for solving mathematical problems and understanding relationships between quantities. Understanding these properties of ratios helps in simplifying complex ratio problems, and ensuring correct comparisons and conversions.

Simple Ratio

It is the most basic form of ratio. It compares two terms directly.

The ratio of a and b can be written as a : b.

Inverse Ratio

In an inverse ratio, the antecedent becomes consequent and the consequent becomes antecedent of the original ratio.

The inverse ratio of a : b is b : a.

Continued Ratio

If there are three or more ratios, then it is called a continued ratio.

a : b : c is a continued ratio.

Equivalent Ratio

Equivalent ratios represent the same relationship between quantities, even though the actual numbers may differ. They can be obtained by multiplying or dividing both terms of the ratio by the same number.

2 : 3 and 6 : 9 are equivalent ratios as the if we divide 6 and 9 with their GCD 3, then we will get 2 : 3.

Componendo

If $\frac{a}{b}$ = $\frac{c}{d}$, then we can add the denominator of each fraction with the numerator of that fraction and write it again. $\frac{a+b}{b}$ = $\frac{c+d}{d}$ This process is called componendo.

If $\frac{2}{3}=\frac{4}{6}$, then $\frac{2+3}{3}=\frac{4+6}{6}⇒\frac{5}{3}=\frac{10}{6}$

Dividendo

If $\frac{a}{b}$ = $\frac{c}{d}$, then we can subtract the denominator of each fraction from the numerator of that fraction and write it again. $\frac{a-b}{b}$ = $\frac{c-d}{d}$ This process is called Dividendo.

If $\frac{2}{3}=\frac{4}{6}$, then $\frac{2-3}{3}=\frac{4-6}{6}⇒\frac{-1}{3}=\frac{-2}{6}$

Componendo and Dividendo

This is a combined process of the above two processes.

If $\frac{a}{b}$ = $\frac{c}{d}$, then we can add the denominator of each fraction with the numerator of that fraction and subtract the denominator from the numerator in the denominator part.

$\frac{a+b}{a-b}$ = $\frac{c+d}{c-d}$

This process is called Componendo and Dividendo.

If $\frac{2}{3}=\frac{4}{6}$, then $\frac{2+3}{2-3}=\frac{4+6}{4-6}⇒\frac{5}{-1}=\frac{10}{-2}$

Duplicate Ratio

If a ratio is $\frac{a}{b}$, then we square the numerator and denominator and write it again. $\frac{a^2}{b^2}$. It is a duplicate ratio of $\frac{a}{b}$.

$\frac{4}{9}$ is the duplicate ratio of $\frac{2}{3}$.

Triplicate Ratio

If a ratio is $\frac{a}{b}$, then we cube the numerator and denominator and write it again. $\frac{a^3}{b^3}$. It is a triplicate ratio of $\frac{a}{b}$.

$\frac{8}{27}$ is the triplicate ratio of $\frac{2}{3}$.

Sub Duplicate Ratio

If a ratio is $\frac{a}{b}$, then we square root the numerator and denominator and write it again. $\frac{\sqrt a}{\sqrt b}$. It is a sub-duplicate ratio of $\frac{a}{b}$.

$\frac{2}{3}$ is the sub-duplicate ratio of $\frac{4}{9}$.

Sub Triplicate Ratio

If a ratio is $\frac{a}{b}$, then we cube root the numerator and denominator and write it again. $\frac{\sqrt [3] {a}}{\sqrt [3] {b}}$. It is a sub-triplicate ratio of $\frac{a}{b}$.

$\frac{2}{3}$ is the sub-triplicate ratio of $\frac{8}{27}$.

Compounded Ratio

If two or more ratios are given, we can form the compounded ratio by multiplying the antecedents together and the consequents together.

When three ratios, a : b, m : n, and x : y are given, the compounded ratio is expressed as amx : bny.

Compounded ratio of $\frac{2}{3},\frac{4}{9},$ and $\frac{3}{5}$ is $\frac{2×4×3}{3×9×5}= \frac{24}{135}$

Problems on ages

We can use ratios to solve problems involving age. Suppose the ratio of ages and the total age are given. First, we express the ratio terms using a variable. Then, we calculate the value of the variable using an algebraic method.

For example, if the age ratio of a father and son is 4 : 1, we can express their ages using the variable x. The father's age would be 4x, and the son's age would be x.

Example:

The ratio of the present ages of the two boys is 3 : 4. After 3 years, the ratio of their ages will be 4 : 5. The ratio of their ages after 21 years will be:

Let the present age of boys be $3x$ years and $4x$ years respectively.

According to the given condition:

After 3 years,

$⇒\frac{3x+3}{4x+3}=\frac{4}{5}$

$⇒ 15x+15 = 16x+12$

$\therefore x = 3$

So, the present age of boys is 9 years and 12 years respectively.

Therefore, the ratio of their age after 21 years is $=\frac{9+21}{12+21}$

$=\frac{30}{33}$

$=\frac{10}{11}$

Thus, the ratio of the age after 21 years is $10:11$.

Hence, the correct answer is $10:11$.

Summary of the formulae used

Tips and Tricks

• If we multiply or divide the antecedent and consequence with the same number, then the ratio will be the same.

• Simplify the ratio to its lowest terms by dividing both terms by their GCD(Greatest Common Divisor).

• To compare both ratios, find the LCM(Least Common Multiple) of the denominators and multiply the ratios with it.

• To solve the problem of age, use a variable to express the terms of the ratio.

• To find an equivalent ratio, multiply or divide both terms by the same number.

Practice Questions

Q1. Two numbers are in the ratio 3 : 5. If 6 is added to each of them the ratio becomes 2 : 3. The numbers are:

1. 21 and 35

2. 30 and 50

3. 24 and 40

4. 18 and 30

Hint: Let the numbers be $3x$ and $6x$, then make the equation $\frac{3x+6}{5x+6}$ = $\frac{2}{3}$.

Answer:

Let the numbers be $3x$ and $6x$.

According to the question,

$\frac{3x+6}{5x+6}$ = $\frac{2}{3}$

$⇒ 9x+ 18 = 10x + 12$

$\therefore x= 6$

Therefore, the numbers are (3 × 6) = 18 and (5 × 6) = 30

Hence, the correct answer is 18 and 30.

Q2. If $\frac{\sqrt{5+x}+\sqrt{5-x}}{\sqrt{5+x}-\sqrt{5-x}}=3$, what is the value of $x$?

1. $\frac{5}{2}$

2. $\frac{25}{3}$

3. 4

4. 3

Hint: Take $a=\sqrt{5+x}+\sqrt{5-x}$, $b=\sqrt{5+x}-\sqrt{5-x}, m=3$ and $n=1$.

Now, apply the rule of componendo and dividendo,

If $\frac{a}{b}=\frac{m}{n}$, then $\frac{a+b}{a-b}=\frac{m+n}{m-n}$

Answer:

Given:

$\frac{\sqrt{5+x}+\sqrt{5-x}}{\sqrt{5+x}-\sqrt{5-x}}=3$

Take $a=(\sqrt{5+x}+\sqrt{5-x})$, $b=(\sqrt{5+x}-\sqrt{5-x}), m=3$ and $n=1$.

Applying the rule of componendo and dividendo,

$\frac{a}{b}=\frac{m}{n}$ ⇒ $\frac{a+b}{a-b}=\frac{m+n}{m-n}$

Now, $\frac{\sqrt{5+x}+\sqrt{5-x}}{\sqrt{5+x}-\sqrt{5-x}}=3$

⇒ $\frac{\sqrt{5+x}+\sqrt{5-x}+\sqrt{5+x}-\sqrt{5-x}}{\sqrt{5+x}+\sqrt{5-x}- \sqrt{5+x}+\sqrt{5-x}}=\frac{3+1}{3-1}$

⇒ $\frac{\sqrt{5+x}+\sqrt{5+x}}{\sqrt{5-x}+\sqrt{5-x}}=\frac{4}{2}$

⇒ $\frac{2\sqrt{5+x}}{2\sqrt{5-x}}=\frac{4}{2}$

⇒ $\frac{\sqrt{5+x}}{\sqrt{5-x}}=2$

Squaring both sides, we get,

⇒ $\left(\frac{\sqrt{5+x}}{\sqrt{5-x}}\right)^{2}=2^{2}$

⇒ $\frac{5+x}{5-x}=4$

⇒ $5+x=20-4x$

⇒ $5x=15$

$\therefore x=3$

Hence, the correct answer is 3.

Q3. In a mixture of 25 litres, the ratio of milk to water is 4 : 1. Another 3 litres of water is added to the mixture. The ratio of milk to water in the new mixture is:

1. 5 : 1

2. 5 : 2

3. 5 : 3

4. 5 : 4

Hint: First, calculate the quantity of milk and water in the mixture, then add 3 litres to the water and find the new ratio.

Answer:

The total quantity of the mixture is 25 litres.

Milk : Water = 4 : 1

Milk = $\frac{4}{5}$ × 25 = 20 litres, Water = $\frac{1}{5}$ × 25 = 5 litres

If 3 litres of water are added then the ratio becomes = 20 : (5 + 3) = 20 : 8 = 5 : 2

Hence, the correct answer is 5 : 2.

Q4. The ratio of A's age to B's age is $4:3$. A will be 26 years old after 6 years. The age of B now is:

1. $19\frac{1}{2}$ years

2. 12 years

3. 21 years

4. 15 years

Hint: Let the present ages of A and B be $4x$ and $3x$ respectively. According to the question, $4x + 6 = 26$, solve this to find $x$ and evaluate the age of B.

Answer:

Let the present ages of A and B be $4x$ and $3x$ respectively.

According to the question,

$4x + 6 = 26$

⇒ $4x = 20$

$\therefore x = 5$

So, the present age of B = 3 × 5 = 15 years

Hence, the correct answer is $15$ years.

Q5. Rs. 782 is divided into three parts in the ratio $\frac{1}{2}:\frac{2}{3}:\frac{3}{4}$. The first part is:

1. Rs. 182

2. Rs. 204

3. Rs. 190

4. Rs. 292

Hint: Use the concept of conversion of fractions to ratios.

Answer:

Given ratio = $\frac{1}{2} : \frac{2}{3} : \frac{3}{4}$

LCM of 2, 3 and 4 = 12

Now, multiplying all ratios by 12, we get,

$(\frac{1}{2} × 12) : (\frac{2}{3} × 12) : (\frac{3}{4} × 12)$

$=6 : 8 : 9$

The sum of the terms of the ratio = 6 + 8 + 9 = 23

$\therefore$ 1st part $=\frac{6}{23} × 782 = 204$

Hence, the correct answer is Rs. 204.

Q6. The ratio of the present ages of R and S is 11 : 17. 11 years ago, the ratio of their ages was 11 : 20. What is R's present age (in years)?

1. 51

2. 33

3. 22

4. 40

Hint: Let the present age of R be $11x$, and S be $17x$.

According to the given condition,

$\frac{11x-11}{17x-11}=\frac{11}{20}$

Answer:

Let the present age of R be $11x$, and S be $17x$.

According to the given condition,

$\frac{11x-11}{17x-11} = \frac{11}{20}$

⇒ $220x - 220 = 187x-121$

⇒ $33x = 99$

$\therefore x = 3$

Thus, the present age of R = 11 × 3 = 33 years

Hence, the correct answer is 33 years.

Q7. The reciprocals of the squares of the numbers 1$\frac{1}{2}$ and 1$\frac{1}{3}$ are in the ratio:

1. 64 : 81

2. 8 : 9

3. 81 : 64

4. 9 : 85

Hint: Convert the given mixed fractions into improper fractions, then evaluate the required ratio.

Answer:

$1\frac{1}{2} : 1\frac{1}{3}$

$=\frac{3}{2}$ : $\frac{4}{3}$

After squaring the fractions, we get,

⇒ $\frac{9}{4}:\frac{16}{9}$

Their reciprocals are,

⇒ $\frac{4}{9}:\frac{9}{16}$

Multiply each ratio by 144 (LCM of 9 and 16)

$\therefore$ The required ratio = 64 : 81

Hence, the correct answer is 64 : 81.

Q8. The railway fares for air-conditioned sleepers and ordinary sleeper classes are in the ratio of 4 : 1. The number of passengers travelling by air-conditioned sleeper and ordinary sleeper classes was in the ratio of 3 : 25. If the total collection was Rs. 37000. How much did air-conditioned sleeper passengers pay?

1. Rs. 15000

2. Rs. 10000

3. Rs. 12000

4. Rs. 16000

Hint: Corresponding compounding ratio = (4 × 3) : (1 × 25) = 12 : 25

Answer:

The ratio of fares for air-conditioned classes to ordinary classes = 4 : 1

The ratio of the number of passengers in air-conditioned classes to ordinary classes = 3 : 25

Corresponding compounding ratio = (4 × 3) : (1 × 25) = 12 : 25

The sum of the terms of the ratio = 12 + 25 = 37

The total collection was Rs. 37000.

Total fare of the passengers in air-conditioned sleeper classes = $\frac{12}{37}$ × 37000 = 12000

Hence, the correct answer is Rs. 12000.

Q9. The compound ratio of the inverse ratio of the ratios $x:yz, y:xz$ and $z:xy$ is:

1. $1:xyz$

2. $xyz:1$

3. $1 : 1$

4. $x:yz$

Hint: The inverse of $a$ is $\frac{1}{a}$ and a compound ratio is the ratio obtained when we compound two or more ratios through multiplication. For two ratios $m:n$ and $p:q$, the compound ratio is $mp:nq$.

Answer:

The inverse of $a$ is $\frac{1}{a}$ and a compound ratio is the ratio obtained when we compound two or more ratios through multiplication.

For two ratios $m:n$ and $p:q$, the compound ratio is $mp:nq$.

The inverse ratio of the ratios,

$x:yz,y:xz$ and $z:xy$ is $yz:x,xz:y$ and $xy:z$, respectively.

$\therefore$ Their compound ratio = $(yz×xz×xy) : (xyz)=xyz:1$

Hence, the correct answer is $xyz:1$.

Q10. If $(x+\frac{1}{x}):(x-\frac{1}{x})=5 : 3$, then the value(s) of $x$ is/are:

1. $\pm 1$

2. $\pm 2$

3. $\pm 3$

4. 0

Hint: By using Componendo and Dividendo rule, $a:b = c:d ⇒ \frac{a+b}{a–b}=\frac{c+d}{c–d}$

Answer:

Given: $(x+\frac{1}{x}):(x-\frac{1}{x})=5:3$

By using Componendo and Dividendo rule, $a:b = c:d ⇒ \frac{a+b}{a–b}=\frac{c+d}{c–d}$,

where $a=x,b=\frac{1}{x},c=5,$ and $d=3$

By putting the given value of a, b, c, d in the formula, we get:

$\frac{x+\frac{1}{x}+x-\frac{1}{x}}{x+\frac{1}{x}-x+\frac{1}{x}}=\frac{5+3}{5-3}$

⇒ $\frac{2x}{\frac{2}{x}}=\frac{8}{2}$

⇒ $x^{2}=4$

$\therefore x=\pm 2$

Hence, the correct answer is $\pm2$.