Concept of Relative Speed and Average Speed: Questions, Examples

Relative speed and average speed are two key concepts in understanding motion. The rate at which one object moves in relation to another is called Relative speed. In problems involving time and distance, relative speed is crucial for determining how fast two moving objects approach or move away from each other. What is relative speed in this context can be illustrated by considering two cars travelling towards each other or in the same direction. Relative speed in physics similarly describes the motion of one object relative to another, whether they are moving in the same or opposite directions. The relative speed concept in time and distance helps us to solve problems where the interaction between two moving entities is analysed.

Average speed can be calculated by dividing the total distance travelled by the total time taken, providing a single value representing an object's overall speed throughout its journey. Understanding what is relative speed in time and distance and average speed is essential for solving various mathematical problems effectively.

What is Relative Speed?

Relative speed is a very key concept in Mathematics. In general the term “Relative” means comparative or in comparison to. This concept is used to determine the effective speed of two moving objects. It depends on the speed and direction of both objects.

Relative speed can be used in the context of

• Two objects or bodies moving towards each other

• Two objects or bodies moving away from each other

• Two objects or bodies moving in the same direction

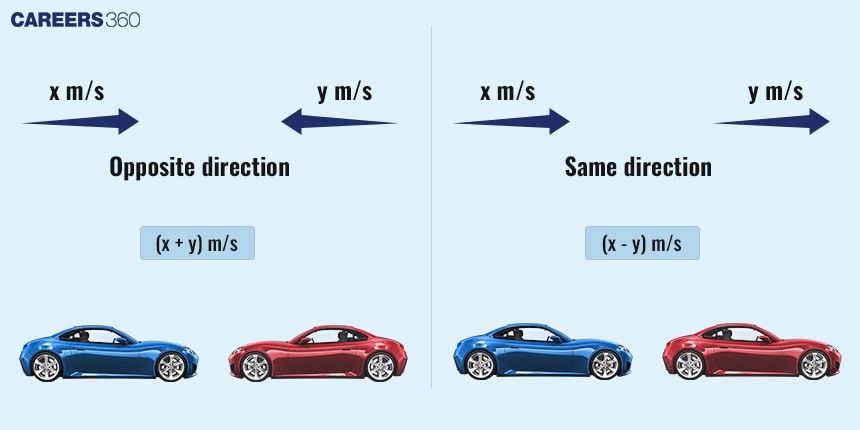
Example:

A rides his bicycle at 15 km/hr, while B starts his ride after 6 hours to catch A at a speed of 25 km/hr. Time taken by B to catch A (in hours) is:

Sol: Distance travelled by A = Speed × Time

So, Distance = 15 × 6 = 90 km

Relative speed of B to A = Speed of B – Speed of A

Relative speed = (25 – 15) km/hr = 10 km/hr

Time taken by B to catch A = $\frac{\text{Distance}}{\text{Relative speed}}$ = $\frac{90}{10}$ = 9 hours

Relative Speed when two bodies are moving in opposite direction

Relative speed when two bodies move in the opposite direction can be calculated by adding their speeds.

Suppose Train A with a speed of $x$ km/hr comes towards Train B with a $y$ km/hr speed.

Then their relative speed will be $(x + y)$ km/hr.

The time both trains have taken to cross or meet each other can be calculated by dividing the total distance between them by the relative speed of the trains.

Time taken = $\frac{\text{Total distance}}{\text{Their Relative Speed} }$

Let the total distance between the two trains be $d$.

Then, time taken = $\frac{d}{x+y}$

Example:

Two donkeys are standing 400 metres apart. The first donkey can run at a speed of 3 m/sec and the second can run at 2 m/sec. If two donkeys run towards each other, after how much time (in seconds) will they bump into each other?

Sol: Here the distance between two donkeys = 400 metres.

Speed of the first donkey = 3 m/sec.

Speed of the second donkey = 2 m/sec.

If both running in opposite directions relative speed = (3 + 2) = 5 m/sec.

So, the time taken to bump into each other = $\frac{400}{5}=80$ sec.

Hence, the correct answer is 80.

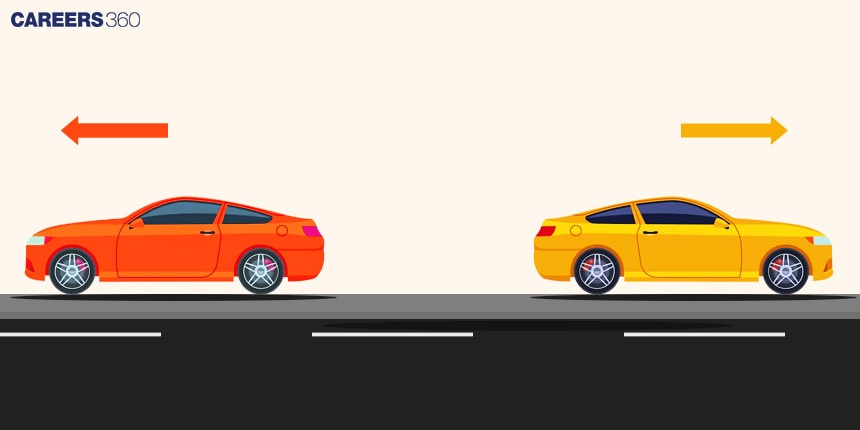
Relative speed when two bodies are moving away from each other can be calculated by adding their speeds.

Suppose Car A with a speed of $x$ km/hr moves away from Train B with a speed of $y$ km/hr.

Then their relative speed will be $(x + y)$ km/hr.

The time both cars have taken to cross each other can be calculated by dividing the sum of the lengths of the two cars by the relative speed of the cars.

Let the combined length of two cars be d.

Then, time taken = $\frac{d}{x+y}$

Example:

Amit and Sumit start walking from the same point in opposite directions at speeds of 6 km/hr and 4 km/hr, respectively. How far will they be from each other after 4 hours?

Sol: Amit and Sumit start walking from the same point in opposite directions at speeds of 6 km/hr and 4 km/hr, respectively.

Their relative speed = 6 + 4 = 10 km/hr

So, in 4 hours, they will travel = 4 × 10 = 40 km

Hence, the correct answer is 40 km.

Relative Speed when two bodies are moving in the same direction

Relative speed when two bodies move in the same direction can be calculated by subtracting the lesser speed from the higher speed.

Suppose Train A with a speed of $x$ km/hr going in the same direction as Train B with a speed of $y$ km/hr.

Then their relative speed will be $(x - y)$ km/hr. $(x > y)$

The time both trains have taken to reach a certain distance can be calculated by dividing the distance by the relative speed of the trains.

Let that distance be $d$.

Then, time taken = $\frac{d}{x-y}$

If two trains are going in the same direction and they are apart from each other for m km, then the faster train with speed x km/hr will catch the slower train with speed y km/hr in $\frac{m}{x-y}$ hours.

Example:

Two trains of equal length are running on parallel lines in the same direction at 46 km/hr and 36 km/hr. The faster train passes the slower train in 36 seconds. The length of each train is:

Sol: Let the length of each train be $x$ m.

During the crossing, the two trains cover a distance equal to the sum of their lengths.

Then, the distance covered = $2x$ m

Relative speed = 46 − 36 = 10 km/hr = 10 × $\frac{5}{18} =\frac{25}{9}$ m/s

$\text{Speed}=\frac{\text{Distance}}{{\text{Time}}}$

⇒ $\frac{25}{9}=\frac{2x}{36}$

$\therefore x=$ 50 m

Hence, the correct answer is 50 m.

What is the average speed?

In general, average means the mean or middle term. So, average speed means the mean average during the whole journey. During a journey, speed may vary from time to time. So it is very important to find out the average speed to complete the journey.

It is generally calculated by dividing the total distance travelled by the total time taken in that journey.

Average speed = $\frac{\text{Total distance}}{\text{Total time}}$

If Kushal goes 20 km on foot in 6 hours and 60 km on a bike in 2 hours, then Kushal’s average speed during the journey is = $\frac{20+60}{6+2}$ = 10 km/hr

There are two special cases where we calculate Average speed:

• When distance is constant

• When time is constant

Example:

A person covers the first 30 km in 60 minutes and the next 40 km in 30 minutes. What is his average speed for the whole journey?

Sol: Given: A person covers the first 30 km in 60 minutes and the next 40 km in 30 minutes.

The total time taken = 1 + $\frac{30}{60}$ = 1 + $\frac{1}{2} = \frac{3}{2}$ hr

The total distance = 30 + 40 = 70 km.

The average speed for the whole journey = $\frac{\text{The total distance}}{\text{The total time taken}}=\frac{70}{\frac{3}{2}}=\frac{70\times2}{3}=\frac{140}{3}$ km/hr

Hence, the correct answer is $\frac{140}{3}$ km/hr.

Average speed when equal distances are covered with two different speeds

If a body covers an equal distance with different speeds, then the average speed of the journey will be the harmonic mean of the speeds.

If A goes to school which is at a distance d at a speed of $x$ km/hr and comes back with a speed of $y$ km/hr, then the average speed during this journey will be $\frac{2xy}{x+y}$

Also, it can be written like, average speed = $\frac{\text{2 × speed 1 × speed 2}}{\text{speed 1 + speed 2}}$

We can derive this formula using the original average speed formula.

Total distance = $d + d$ = $2d$

Speed of A going to school = $\frac{d}{x}$

Speed of A coming back from school = $\frac{d}{y}$

Total time = $\frac{d}{x}+\frac{d}{y}$

So, average speed = $\frac{\text{Total distance}}{\text{Total time}}=\frac{2d}{\frac{d}{x}+\frac{d}{y}}=\frac{2xy}{x+y}$

So, the above formula is right.

Example:

A boat goes a certain distance at 30 km/hr and comes back the same distance at 60 km/hr. What is the average speed (in km/hr) for the total journey?

Sol: Average speed = $\frac{2xy}{x+y}$, where $x$ and $y$ are two given speeds of the boat (for the same distance).

Putting the values $x$ = 30 and $y$ = 60, we get,

$\therefore$ Average speed = $\frac{2×30×60}{30+60}$ = $\frac{3600}{90}$ = 40 km/hr

Hence, the correct answer is 40 km/hr.

Average speed when a body moves for an equal time period with two different speeds

If the time period is the same or constant each time, and the body is moving at different speeds, then finding the average speed is very easy. The arithmetic mean of the speeds will be the average speed.

Suppose a boy moving with speed $x$ km/hr for $t$ hours and $y$ km/hr for the same $t$ hours,

then average speed = $\frac{x+y}{2}$

It can be derived.

In t hours with speed $x$ km/hr, the boy travels $xt$ km.

Again in t hours with speed $y$ km/hr, boy travels $yt$ km.

Total distance = $t(x+y)$

Total time taken = $t + t$ = $2t$

So, average speed = $\frac{\text{Total distance}}{\text{Total time}}= \frac{t(x+y)}{2t}=\frac{x+y}{2}$

So, the above formula is right.

Example:

A car travels for 1 hour at 70 km/hr and travels for another hour at 30 km/hr. Find the average speed for the total journey.

Sol: Average speed for the whole journey = $\frac{70+30}{2}$ = 50 km/hr

Tips and Tricks

• Relative speed when two bodies move in the opposite direction can be calculated by adding their speeds.

• Relative speed when two bodies move in the same direction can be calculated by subtracting the lesser speed from the higher speed.

• Relative speed when two bodies are moving away from each other can be calculated by adding their speeds.

• Average speed = $\frac{\text{Total distance}}{\text{Total time}}$

• Average speed = $\frac{2xy}{x+y}$, where $x$ and $y$ are two given speeds (for the same distance)

• When two objects move towards each other, the time they will meet = $\frac{\text{Total distance}}{\text{Their Relative Speed} }$

Practice Questions

Q1. Two people, A and B, are at a distance of 260 km from each other at 9:00 a.m. A immediately starts moving towards B at a speed of 25 km/hr at 11:00 a.m., B starts moving towards A at a speed of 10 km/hr. At what time (in p.m.) will they meet each other?

1. 5:00

2. 6:00

3. 6:30

4. 7:00

Hint: When two persons move toward each other, their relative speed is the sum of their speeds.

Answer:

Given:

A's speed = 25 km/hr

B' speed = 10 km/hr

Distance traveled by A from 9 a.m. to 11 a.m. or in 2 hours

= 25 × 2 = 50 km

Remaining distance = (260 – 50) = 210 km

When two persons move toward each other, their relative speed is the sum of their speeds.

So, relative speed = 25 + 10 = 35 km/hr

Time taken by them to cover the remaining 210 km = $\frac{210}{35}$ = 6 hours

So, they will meet at 6 hours from 11 a.m. i.e. at 5 p.m.

Hence, the correct answer is 5:00.

Q2. A policeman chases a thief. The speeds of the policeman and the thief are 8 km/hr and 6 km/hr, respectively. If the policeman starts 10 minutes late, at what distance he will catch the thief?

1. 6 km

2. 8 km

3. 4 km

4. 2 km

Hint: The relative speed of the thief and the policeman running in the same direction = Speed of the policeman – Speed of the thief

Answer:

The thief starts running and the policeman chases him after 10 minutes.

The thief and the policeman run 6 km/hr and 8 km/hr, respectively.

Their relative speed $=8 - 6= 2$ km/hr

Distance covered by the thief in 10 minutes = $6\times \frac{10}{60} = 1$ km

Time required to catch the thief = $\frac{1}{2} = 0.5$ hour

$\therefore$ Distance covered by the policeman in 0.5 hours = $0.5 \times8 = 4$ km

So, the policeman will catch the thief at 4 km.

Hence, the correct answer is 4 km.

Q3. Anil and Tirath drove between two points, A and B, 192 km apart. Anil started the journey from point A at 8:20 am, drove at a speed of 64 km/hr, reached point B, and immediately returned to A at the same speed. Tirath started the journey from point A at 9:50 am, drove at a speed of 96 km/hr, reached point B, and immediately returned to A at the same speed. At what time did Anil and Tirath first meet each other?

1. 11:38 am

2. 11:28 am

3. 11:43 am

4. 11:33 am

Hint: The relative speed of two people running in opposite directions is the sum of their speeds.

Answer:

Given: The distance between points A and B is 192 km.

Anil's speed is 64 km/hr.

So, it will take $\frac{192}{64} = 3$ hours for Anil to reach point B.

He started at 8:20 am. So, he will reach point B at 8:20 + 3 = 11:20 am

Tirath's speed is 96 km/hr.

Since Tirath starts his journey at 9:50 am,

At 11:20, when Anil reaches point B, Tirath will be (96 × 1.5) = 144 km from A.

Now, at 11:20, the distance between Anil and Tirath is (192 – 144) = 48 km

Their relative speed is (64 + 96) = 160 km/hr

So, they will meet after $\frac{60 × 48}{160} =18$ minutes

Therefore, Tirath and Anil will meet each other at (11:20 + 18) = 11:38 am

Hence, the correct answer is 11:38 am.

Q4. Ramesh, on his way to his hometown, travelled the first 250 km at a speed of 75 km/hr and the next 250 km at a speed of 85 km/hr. Find the average speed for the whole journey (correct to 2 decimal places).

1. 80.55 km/hr

2. 79.69 km/hr

3. 79.20 km/hr

4. 80.69 km/hr

Hint: Average speed for the whole journey = $\frac{\text{Total distance}}{\text{Total time taken on journey}}$

Answer:

Given: Ramesh travelled the first $250$ km at $75$ km/hr.

So, the time taken was $\frac{250}{75}=\frac{10}{3}$ hr

The next $250$ km were covered at the speed of $85$ km/hr.

So, the time taken was $\frac{250}{85}=\frac{50}{17}$ hr

Average speed for the whole journey

$=\frac{\text{Total distance}}{\text{Total time taken on journey}}$

$=\frac{250+250}{\frac{10}{3} + \frac{50}{17} }$

$=500×\frac{51}{320}$

$=79.69$ km/hr

Hence, the correct answer is 79.69 km/hr.

Q5. A man covers a total distance of 100 kilometres on a bicycle. For the first 2 hours, the speed was 20 km/hr and for the rest of the journey, it came down to 10 km/hr. The average speed will be:

1. $12\frac{1}{2}\ \text{km/hr}$

2. $13\ \text{km/hr}$

3. $15\frac{1}{8}\ \text{km/hr}$

4. $20\ \text{km/hr}$

Hint: Use these formulas:

Distance = Speed × Time

Average speed = $\frac{\text{Total distance}}{\text{Total time}}$

Answer:

Given:

Total distance = 100 km

The distance covered in the first 2 hours at 20 km/hr:

Distance = Speed × Time = 20 × 2 = 40 km

Distance left to cover is (100 – 40) = 60 km

Time taken to cover the remaining 60 km at a speed of 10 km/hr:

Time for the rest of the journey = $\frac{\text{Distance}}{\text{Speed}}=\frac{60}{10}$ = 6 hours

Total time taken = 2 hours + 6 hours = 8 hours

Average speed = $\frac{\text{Total distance}}{\text{Total time}}=\frac{100}{8}=12\frac{1}{2}\ \text{km/hr}$

Hence, the correct answer is $12\frac{1}{2}\ \text{km/hr}$.

Q6. A man travels 50 km at 25 km/hr, the next 40 km at 20 km/hr, and then 90 km at 15 km/hr. His average speed is:

1. 18 km/hr

2. 25 km/hr

3. 20 km/hr

4. 15 km/hr

Hint: Use the formula: Average Speed = $\frac{\text{Total distance}}{\text{Total time}}$

Answer:

Given:

A man travels the first 50 km at 25 km/hr, the next 40 km at 20 km/hr and the last 90 km at 15 km/hr.

Time taken to travel 50 km = $\frac{50}{25}$ = 2 hours

Time taken to travel 40 km = $\frac{40}{20}$ = 2 hours

Time taken to travel 90 km = $\frac{90}{15}$ = 6 hours

Total distance = (50 + 40 + 90) = 180 km

Total time = (2 + 2 + 6) = 10 hours

Average speed $=\frac{\text{Total distance}}{\text{Total time}}=\frac{180}{10}=$ 18 km/hr

Hence, the correct answer is 18 km/hr.

Q7. A and B are 15 km apart and when travelling towards each other, meet after half an hour, whereas they meet two and a half hours later if they travel in the same direction. The faster of the two travels at a speed of:

1. 15 km/hr

2. 18 km/hr

3. 10 km/hr

4. 8 km/hr

Hint: Use the concept of relative speed and the formula: Relative Speed = $\frac{\text{Relative disatnce}}{\text{Time}}$.

Answer:

Let the speeds of A and B be $a$ km/h and $b$ km/h respectively.

When moving on opposite sides, relative speed = $(a + b)$ km/h.

When moving on the same sides, relative speed = $(a – b)$ km/h.

According to the question, (Using: Relative speed = $\frac{\text{Relative disatnce}}{\text{Time}}$)

$a + b = \frac{15}{\frac{1}{2}}$

⇒ $a + b = 30$ -------------------------------------------(1)

Also $a – b = \frac{15}{2\frac{1}{2}}$

⇒ $a – b = 6$ ---------------------------------------------(2)

By solving equation 1 and equation 2 we get,

$a$ = 18 km/h and $b$ = 12 km/h

So, the faster of the two travels at a speed of 18 km/h.

Hence, the correct answer is 18 km/h.

Q8. A car moving in the morning fog passes a man walking at 4 km/hr in the same direction. The man can see the car for 3 minutes and visibility is up to a distance of 130 m. The speed of the car is:

1. $7\frac{3}{5}$ km/hr

2. $6\frac{3}{5}$km/hr

3. $7$ km/hr

4. $5$ km/hr

Hint: Use the formulae:

When moving in the same direction, relative speed = S1 – S2

Speed = $\frac{\text{Distance}}{\text{Time}}$

Answer:

Speed of man = 4 km/hr

Let $x$ be the speed of the car.

As they are moving in the same direction, relative speed = $(x-4)$ km/hr

⇒ Distance, $d$ = $\frac{130}{1000}$km = 0.13 km

⇒ Time, $t$ = $\frac{3}{60}$hr = 0.05 hr

So, Speed = $\frac{\text{Distance}}{\text{Time}}$

⇒ $(x-4)$ = $\frac{0.13}{0.05}$

$\therefore x = 4+\frac{13}{5}=\frac{33}{5}=6\frac{3}{5}$ km/hr

Hence, the correct answer is $6\frac{3}{5}$ km/hr.

Q9. A man travels for 14 hours and 40 minutes. He covers half of the journey by train at a rate of 60 km/hr and the rest by road at a rate of 50 km/hr. The distance travelled by him is:

1. 720 km

2. 800 km

3. 960 km

4. 1000 km

Hint: The average speed of $a$ km/h and $b$ km/h is ($\frac{2×a×b}{a+b}$) km/h, if the distance travelled at both speeds, is the same. Use this formula to find the average speed then multiply it with the given time to get the distance.

Answer:

Given:

A man covers half of the journey by train at a rate of 60 km/hr and the rest by road at a rate of 50 km/hr.

So, the average speed of the man = ($\frac{2×60×50}{60+50}$) = $\frac{600}{11}$ km/h

With this average speed, he travels for 14 hours and 40 minutes i.e., 14$\frac{2}{3}$ hours = $\frac{44}{3}$ hours

$\therefore$ The distance travelled by him is = ($\frac{600}{11}$×$\frac{44}{3}$) km = 800 km

Hence, the correct answer is 800 km.

Q10. Two stations L and M are 720 km apart from each other. A train leaves from L to M, and another trains leave from M to L simultaneously. Both trains meet after 24 hours. If the speed of the first train is 10 km/hr more than the second train, then what is the speed of the slower train?

1. 20 km/hr

2. 16 km/hr

3. 14 km/hr

4. 10 km/hr

Hint: By using the formula: Relative speed = $\frac{\text{Distance}}{\text{Time}}$, here the speed is the relative in opposite direction.

Answer:

Distance between L and M = 720 km

Time taken in meeting = 24 hours

Difference of speed of 1st train and 2nd train = 10 km/hr

Let the speed of the faster train be $x$ and the slower train be $x-10$.

Here the speed is the relative speed in the opposite direction

We know that,

Relative speed = $\frac{\text{Distance}}{\text{Time}}$

⇒ $x + x - 1 0 = \frac{720}{24}$

⇒ $2x =30 + 10$

⇒ $x=20$

The speed of the slower train is = 20 – 10 = 10 km/hr

Hence, the correct answer is 10 km/hr.