Remainder Theorem of Polynomial - Definition, Formula, Proof, Examples

In mathematics, the concept of a remainder arises when one number is divided by another. The remainder is the amount left after the division when the divisor does not divide the dividend completely. In this topic, we will discuss ‘remainder theorem’, ‘polynomial remainder theorem’, ‘factor theorem’, ‘remainder theorem formula’, ‘factor and remainder theorem’, ‘factor theorem and remainder theorem’, ‘factor theorem examples’, ‘example of remainder theorem’ and ‘polynomial remainder theorem examples’.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

This Story also Contains

1. Remainder theorem
2. What is a remainder?
3. Some Important theorems related to the remainder
4. Remainder in polynomial
5. Practice Questions

Remainder theorem

To understand the remainder theorem we first need to learn about the dividend, divisor, quotient, remainder, and the relation among them. We will also have an idea about the properties of a remainder and the applications of remainders.

What is a remainder?

If a number (dividend) is not completely divisible by another number (divisor) then we are left with a value after the division is done. This value is called the remainder.

For example, if we divide 25 by 6, then 25 is the dividend, 6 is the divisor, 4 is the quotient and 1 is the remainder.

Remainder formula:

A dividend is a number or value that is divided. A divisor is the value that divides the other number. A quotient is an answer we get when one value is divided by another value, and the remainder is the number that is left when a dividend is not completely divisible by the divisor. The relation between dividend, divisor, quotient, and remainder is:
Dividend = (Divisor × Quotient) + Remainder

We can get the remainder formula from this equation as,

Remainder = Dividend - (Divisor × Quotient)

How do I find the remainder?

Finding the remainder is an easy method. We need to just divide the number by another number with its multiples and get the remainder.

Example: When we divide 44 by 5 we get,

44 = (8 × 5) + 4

So, the remainder is 4.

Properties of remainder:

• A remainder is always less than the divisor.

• If one number (divisor) divides the other number (dividend) completely, then the remainder is 0. It is referred to as a complete division.

• If a dividend is a multiple of the divisor, then the remainder is 0.

Application of remainder:

The applications of the remainder are very useful and important to us, these are as follows:

• Distributing items evenly among groups, leftover items are the remainder.

• Determining next occurrences or intervals, like bus schedules.

• Widely used in modular arithmetic and congruence-type problems.

• Converting time formats, e.g., converting minutes to hours and minutes.

• In algebra, polynomial division results in a quotient and a remainder.

Some Important theorems related to the remainder

Remainders play a fundamental role in number theory and algebra, giving rise to several important theorems. Let’s discuss them one by one:

Basic Remainder theorem

This theorem states that for any integer a and any positive integer b, there exist unique integers q (quotient) and r (remainder) such that:

a = bq + r, where 0 $\leq$ r < b.

Binomial theorem to find the remainder:

As the power increases, the expansion becomes lengthy and tedious to calculate. A binomial expression that has been raised to a very large power can be easily calculated with the help of the Binomial Theorem.

the formula for the Binomial Theorem is as follows:

(a +b)ⁿ = ∑ⁿ_r=0(ⁿ C _r)a^n−r b^r

Where a and b are real numbers, n is a positive integer and C is the co-efficient.

Example: Find the remainder using the binomial theorem when $5^{103}$ is divided by 13.

Sol: $5^{103}$

= $5(5^{102}$

= $5(25^{51}$

= $5(26-1)^{51}$

= 5×∑51r=0 51Cr 2651-r (-1)r

So, the remainder, when ∑51r=0 51Cr 2651-r (-1)r is divided by 13 is

= $5 × (-1)^51$ = -5, as the remainder can’t be (-5), thus when dividing by 13 the required remainder = (-5 + 13) = 8.

Chinese Remainder Theorem:

Given pairwise coprime positive integers $n_1, n_2, n_3, …, n_k$ and arbitrary integers $a_1, a_2, a_3,....., a_k$, the system of simultaneous congruences

$x\equiv a_1$ (mod $n_1$)

$x\equiv a_2$ (mod $n_2$)

.

.

.

$x\equiv a_k$ (mod $n_k$)

has a solution, and the solution: x is unique modulo N = $n_1. n_2. n_3. …n_k$

Euler’s theorem to find the remainder:

Euler's theorem is useful in number theory for finding remainders when dealing with some large exponents. The theorem states that:

If a and n are coprime positive integers, then $a^{\phi(n)}\equiv 1$ (mod $n$).

$\phi(n)$ is the Euler's function = $\phi(n)=n(1-\frac{1}{a})(1-\frac{1}{b})(1-\frac{1}{a})$,

Where a, b, and c are prime factors of n.

Example: Find the remainder when $7^{120}$ is divided by 66.

Sol: Since 7 and 66 are co-prime to each other, we can use Euler’s theorem to find the required remainder.

Here, $\phi(66)=66(1-\frac{1}{2})(1-\frac{1}{3})(1-\frac{1}{11})$ [2, 3, and 11 are the prime factors of 66.]

⇒ $\phi(66) = 66×\frac{1}{2}×\frac{2}{3}×\frac{10}{11} = 20$

Now, we can say that $7^{20}\equiv 1$ (mod $66$)

⇒ $(7^{20})^6\equiv (1)^6$ (mod $66$)

⇒ $7^{120}\equiv 1$ (mod $66$)

Hence, the required remainder is 1.

Fermat's little theorem:

Fermat's Little Theorem states that for any prime number p and any integer a not divisible by p,

$a^{p-1}\equiv 1$ (mod $p$).

This can also be written as $a^{p}\equiv a$ (mod $p$).

Example: Find the remainder when $3^100$ is divided by 7.

Sol: 7 is a prime number and 3 is not divisible by 7.

So, we can say that $3^{7-1}\equiv 1$ (mod 7)

⇒ $3^6\equiv 1$ (mod 7)

⇒ $(3^6)^{16}\equiv (1)^{16}$ (mod 7)

⇒ $3^96\equiv 1$ (mod 7)

⇒ $(3^96)(3^4)\equiv (1)(3^4)$ (mod 7) [multiplying by $3^4$]

⇒ $3^100\equiv 81$ (mod 7)

⇒ $3^100\equiv 4$ (mod 7)

Hence, the remainder when $3^100$ is divided by 7 is 4.

Remainder in polynomial

There are various theorems useful for finding the remainder when a polynomial p(x) is divided by another polynomial q(x). Let’s discuss them one by one.

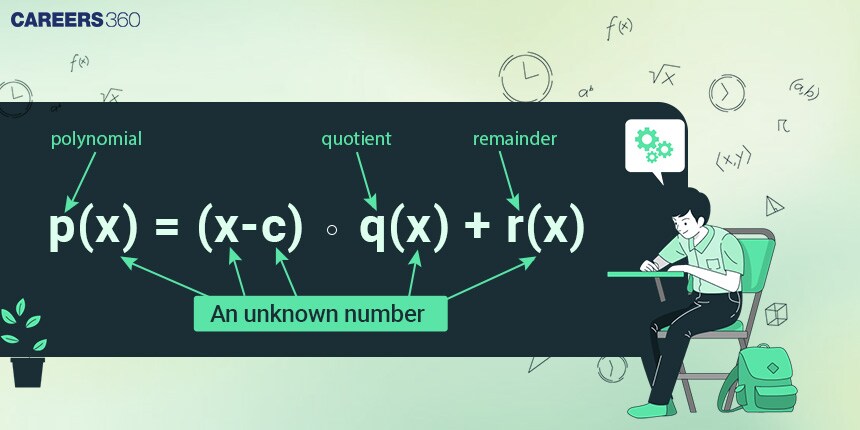
Factor theorem:

The factor theorem states that (x-a) is a factor of p(x) if p(a) = 0

Similarly if p(a) = 0, then (x-a) is a factor of p(x).

Example: Using the factor theorem, check if (x-2) is a factor of f(x) = $2x^2-5x+2$.

Sol: f(x) = $2x^2-5x+2$

Now, f(2) = $2(2)^2 - 5(2)+2$ = 0

So, (x-2) is a factor of f(x).

Remainder theorem:

According to the remainder theorem, when a polynomial p(x) (whose degree is greater than or equal to 1) is divided by a linear polynomial (x - a), the remainder is given by p(a).

Example: Find the remainder when $3x^2+2x+5$ is divided by (x-1).

Sol: Let f(x) = $3x^2+2x+5$

When f(x) is divided by (x-1), the remainder is f(1).

Here, f(1) = $3(1)^2+2(x)+5$ = 3 + 2 + 5 = 10.

So, the required remainder is 10.

Practice Questions

Q.1. A number, when divided by 6, leaves a remainder of 3. When the square of the same number is divided by 6, the remainder is:

1. 0

2. 2

3. 1

4. 3

Hint: Apply the formula: Dividend = Quotient × Divisor + Remainder

Solution:

Let the number be $x$.

Dividend = Quotient × Divisor + Remainder

When divided by 6, $x$ leaves a remainder of 3.

Let the quotient be $q$.

Then, $x=6q+3$

Now, squaring both sides we get,

$x^2=(6q+3)^2$

⇒ $x^2=36q^2+36q+9$

⇒ $x^2=6(6q^2+6q+1)+3$

Thus, $x^2$ divided by 6 leaves 3 as a remainder.

Hence, the correct answer is option (4).

Q.2. Find the remainder when 88 + 6 is divided by 7.

1. 0

2. 2

3. 3

4. 1

Hint: When a number is completely divisible by a number, then the remainder is zero.

Solution:

To find the remainder of $8^{8} + 6$ when divided by 7,

When 88 is divided by 7, the remainder = $\frac{8^8}{7}→R=1^8=1$ (where R is the remainder)

⇒ $8^{8} + 6→R(1+6)→R(7)$

When 7 is divided by 7, there is no remainder.

Hence, the remainder will be option (1).

Q.3. What is the remainder when $\left(x^{17}+1\right)$ is divided by $(x+1)$?

1. $x$

2. $x-1$

3. $0$

4. $1$

Hint: Put the divisor equal to zero to find the value of $x$ and use the remainder theorem.

Solution:

$\left(x^{17}+1\right)$ is divided by $(x +1)$

Let $P(x) = \left(x^{17}+1\right)$

Divisor = $x + 1$

$\therefore$ remainder = $P(- 1) = (- 1)^{17}+ 1= - 1 + 1 = 0$

Hence, the correct answer is option (3).

Q.4. When a number is divided by 45, the remainder is 21. What will be the remainder when the number is divided by 15?

1. 6

2. 5

3. 3

4. 0

Hint: Dividend = divisor × quotient + remainder

Solution:

Let the quotient when the number is divided by 45 be $x$.

Then, the number should be 45$x$ + 21

= (15 × 3$x$) + 21

Let 3$x$ = P.

So, 45$x$ + 21 = 15P + 21

So, it is clear that 15P is completely divisible by 15

So, the remainder should be 21 – 15 = 6.

Hence, the correct answer is option (1).

Q.4. What will be the remainder when 2654081 + 9 is divided by 266?

1. 8

2. 6

3. 1

4. 9

Hint: Substitute 265 with (266 – 1) as it leaves – 1 remainder when divided by 266.

Solution:

We have,

2654081 + 9 or (266 - 1)4081 + 9 is divided by 266.

Dividing 265 by 266 leaves a remainder of – 1.

Since 4081 is an odd number.

So, remainder when 2654081 is divided by 266 = (–1)4081 = – 1

So, final remainder = – 1 + 9 = 8

Hence, the correct answer is option (1).

Q.5. During a division, Pranjal mistakenly took as the dividend a number that was 10% more than the original dividend. He also mistakenly took as the divisor a number that was 25% more than the original divisor. If the correct quotient of the original division problem was 25 and the remainder was 0, what was the quotient that Pranjal obtained, assuming his calculations had no error?

1. 21.25

2. 21.75

3. 22

4. 23

Hint: Assume original dividend be $x$ and divisor be $y$ then use the formula,

(Quotient × Divisor) + Remainder = Dividend.

Solution:

Given:

Original quotient = 25

Original remainder = 0

Let, original dividend be $x$ and divisor be $y$.

We know, Dividend = Quotient × Divisor + Remainder

So, for the number, $25y+0=x$

⇒ $25y=x$

He mistakenly took as the dividend a number that was 10% more than the original dividend.

So, the new dividend is $\frac{110x}{100}=\frac{110×25y}{100}$.

He also mistakenly took as the divisor a number that was 25% more than the original divisor.

So, new divisor = $\frac{125y}{100}$

So, new quotient = $\frac{\frac{110×25y}{100}}{\frac{125y}{100}}=22$

So, the quotient that Pranjal obtained, assuming his calculations had no error is 22.

Hence, the correct answer is option (3).

Q.6. When m is divided by 7, the remainder is 5. When 3m is divided by 7, the remainder is:

1. 3

2. 2

3. 0

4. 1

Hint: Dividend = Quotient × Divisor + Remainder

Solution:

Use: Dividend = Quotient × Divisor + Remainder

If $\mathrm{m}$ divided by 7 gives a remainder of 5, we can express $\mathrm{m}$ as $\mathrm{m} = 7\mathrm{k} + 5$ for some integer $\mathrm{k}$.

Substituting this into $3m$

$3\mathrm{m} = 3(7\mathrm{k} + 5) = 21\mathrm{k} + 15=7(3\mathrm{k}+2)+1$.

So, when $3\mathrm{m}$ is divided by 7, the remainder is 1.

Hence, the correct answer is option (4).

Q.7. The divisor is 10 times the quotient and 5 times the remainder in a division sum. What is the dividend if the remainder is 46?

1. 5972

2. 4286

3. 4874

4. 5336

Hint: Use the relationship to find the required value of the dividend from the given information.

Dividend = (Divisor × Quotient) + Remainder.

Solution:

Given: Remainder is 46 and the divisor is 5 times the remainder.

The divisor = 5 × 46 = 230

The divisor is 10 times the quotient.

The quotient = $\frac{230}{10}$ = 23

Dividend = Divisor × Quotient + Remainder

Dividend = 230 × 23 + 46 = 5290 + 46 = 5336

Hence, the correct answer is option (4).

Q.8. What is the remainder when $3^8$ is divided by 7?

1. 5

2. 2

3. 4

4. 6

Hint: Convert $3^8$ into an exponential of 9 then use that 9 divided by 7 will always leave the remainder 2.

Solution:

To find: The remainder when $3^8$ is divided by 7

= remainder ($\frac{3^8}{7}$)

= remainder ($\frac{(3^2)^4}{7}$)

= remainder ($\frac{(9)^4}{7}$)

9 divided by 7 will leave the remainder of 2.

So, remainder = remainder ($\frac{2^4}{7})$

= remainder ($\frac{16}{7}$)

= 2

Hence, the correct answer is option (2).

Q.9. Two numbers, when divided by a certain divisor, leave the remainder 57. When the sum of the two numbers is divided by the same divisor, the remainder is 49. The divisor is:

1. 65

2. 56

3. 49

4. 27

Hint: Dividend = Divisor × Quotient + Remainder

Solution:

Let the two numbers be $a$ and $b$ and the divisor is $d$.

According to the question,

$a = d×p + 57$ and $b=d×q + 57$, where $p$ and $q$ are the quotients.

Adding these two equations we get,

$(a+b)=d(p+q)+114$

Again when the sum of the two numbers is divided by the same divisor, the remainder is 49.

$\therefore$ Divisor = (114 – 49) = 65

Hence, the correct answer is option (1).

Q.10. Find the remainder when $19^{19}+20$ is divided by 18.

1. 3

2. 2

3. 1

4. 0

Hint: A $\equiv$ B (mod C) means A leaves a remainder of B when divided by C.

Solution:

To find: The remainder when $19^{19}+20$ is divided by 18.

Now, 19 $\equiv$ 1 (mod 18)

⇒ 1919 $\equiv$ 119 (mod 18)

⇒ 1919 $\equiv$ 1 (mod 18)

⇒ (1919 + 20) $\equiv$ (1 + 20) (mod 18)

⇒ (1919 + 20) $\equiv$ (1 + 2) (mod 18) (Since 20 divides by 18 leaves a remainder of 2)

⇒ (1919 + 20) $\equiv$ 3 (mod 18)

So, the remainder when $19^{19}+20$ is divided by 18 is 3.

Hence, the correct answer is option (1).

Q.11. The remainder of the term $9+9^2+\ldots+9^{(2 n+1)}$ when divided by 6 is:

1. 1

2. 4

3. 2

4. 3

Hint: When the sum of an odd number times 3 is divided by 6, the remainder is 3.

Solution:

Given, $9+9^2+\ldots+9^{(2 n+1)}$ is divided by 6

Consider, $9+9^2+\ldots+9^{(2 n+1)}$

Here, for each term in the series, the remainder when divided by 6 is 3.

The sum of the remainder of each term = 3 + 3 + 3 + ............+ up to 2n + 1 terms

2n + 1 is an odd number, so when the sum of an odd number times 3 is divided by 6, the remainder is 3.

Hence, the correct answer is option (4).

Q.12. Find the remainder when we divide $3x^4-2x^2+4x-1$ by $(2x-1)$.

1. $\frac{11}{16}$

2. $\frac{15}{16}$

3. $\frac{13}{16}$

4. $1$

Hint: When a polynomial $f(x)$ is divided by a linear polynomial $(x - a)$, the remainder of that division will be equivalent to $f(a)$.

Solution:

Assume, $2x-1$ = 0

⇒ $x$ = $\frac{1}{2}$

Let $f(x)=3x^4-2x^2+4x-1$

So, the remainder when $3 x^4-2 x^2+4 x-1$ is divided by $(2x-1)$ is $f(\frac{1}{2})$

= $3 (\frac{1}{2})^4-2 (\frac{1}{2})^2+4(\frac{1}{2})-1$

= $\frac{3}{16} - \frac{1}{2} + 2 - 1$

= $\frac{3}{16} + \frac{1}{2}$

= $\frac{11}{16}$

Hence, the correct answer is option (1).

Q.13. Find the remainder when $29^25$ is divided by 11.

1. 5

2. 2

3. 10

4. 9

Hint: Start with $29^{11-1}\equiv 1$ (mod 11).

Solution: 11 is a prime number and 29 is not divisible by 11.

So, using Fermat’s little theorem we can say that $29^{11-1}\equiv 1$ (mod 11)

⇒ $29^{10}\equiv 1$ (mod 11)

⇒ $(29^{10})^2\equiv (1)^5$ (mod 11)

⇒ $(29^{20}×29^{5})\equiv (1×29^{5})$ (mod 11)

⇒ $(29^{25})\equiv 29^{5}$ (mod 11)

⇒ $(29^{25})\equiv (-4)^{5}$ (mod 11)

⇒ $(29^{25})\equiv (-4×256)$ (mod 11)

⇒ $(29^{25})\equiv (-4×3)$ (mod 11)

⇒ $(29^{25})\equiv (-12)$ (mod 11)

⇒ $(29^{25})\equiv (-1)$ (mod 11)

⇒ $(29^{25})\equiv 10$ (mod 11)

So, the required remainder is 10.

Hence, the correct answer is option (3).