Rhombus, Squares, Rectangles and Trapezium: Definition, Formula, Properties

In geometry, quadrilaterals play a crucial role. Rhombus, square, rectangles, and trapezium are such quadrilaterals. This article explains all the aspects of the rhombus, square, rectangles, and trapezium in detail, going through topics such as ‘rhombus area’, ‘rhombus properties’, ‘rhombus area formula’, ‘rhombus shape’, ‘rhombus definition’, ‘rhombus area and perimeter’, ‘Trapezium and area of trapezium’, ‘Square and area of square’, ‘Rectangle and area of rectangle’.

Rhombus, squares, rectangles, and Trapezium: An Overview

• A quadrilateral with four equal sides is called a rhombus.

• A rhombus with all angles being right angles is called a square.

• A quadrilateral with opposite sides equal and all angles being right angles is called a rectangle.

• A quadrilateral with one pair of parallel sides is called a trapezium.

Rhombus

Sides and Angles of a Rhombus

• All four sides are of equal length.

• Opposite angles are equal.

• Adjacent angles are supplementary (sum = 180 degrees).

Perimeter and Area of a rhombus

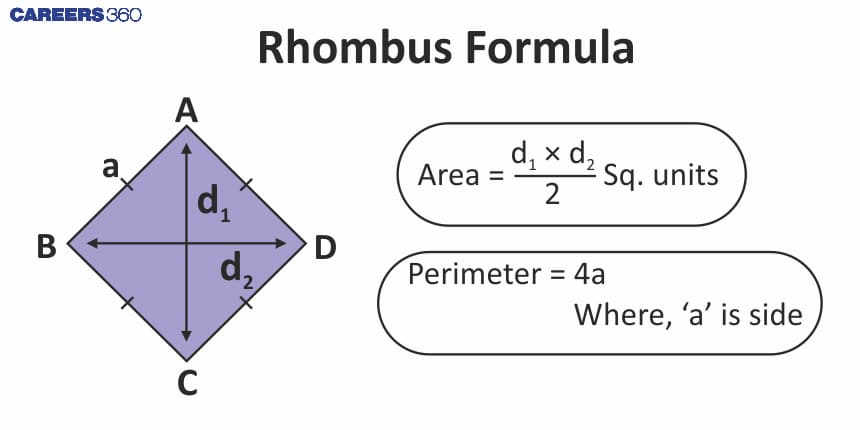
Important Properties of a rhombus

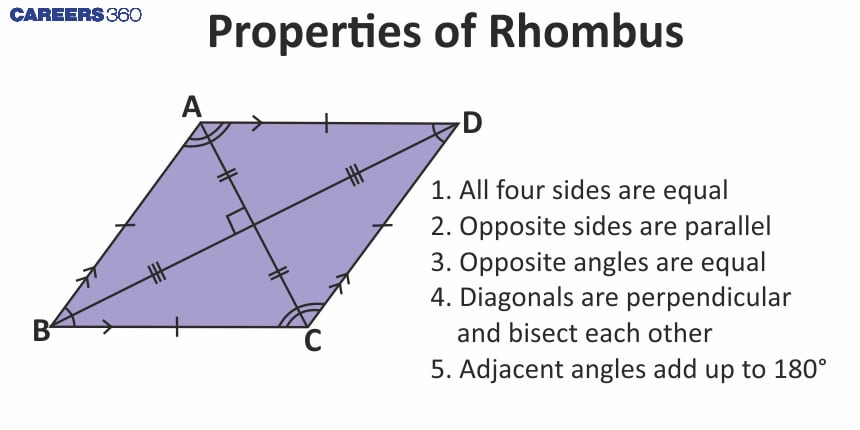
• Diagonals bisect each other at right angles.

• Diagonals bisect the angles of the rhombus.

• Each diagonal divides the rhombus into two congruent triangles.

Sides and Angles of a Square

• All four sides are of equal length.

• All four angles are right angles.

Important Properties of a Square

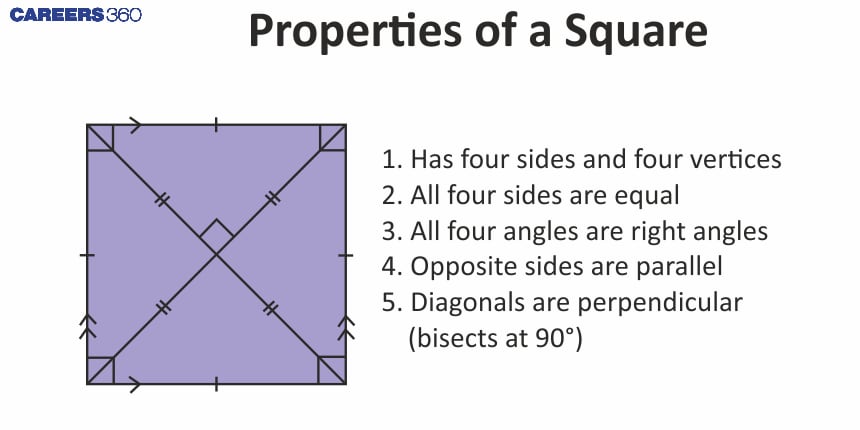
• Diagonals are equal in length and bisect each other at right angles.

• Diagonals bisect the angles of the square.

• A square is a type of rhombus and a type of rectangle.

Rectangle: A general description

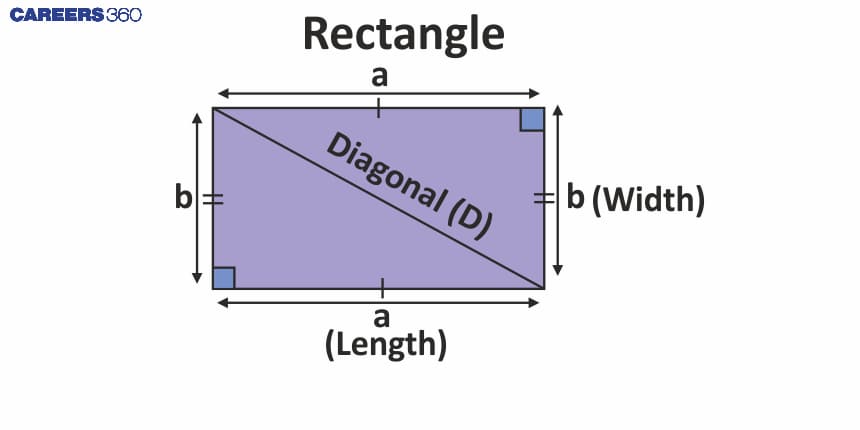
Sides and Angles of a Rectangle

• Opposite sides are equal in length.

• All four angles are right angles (90 degrees).

Important Properties of a Rectangle

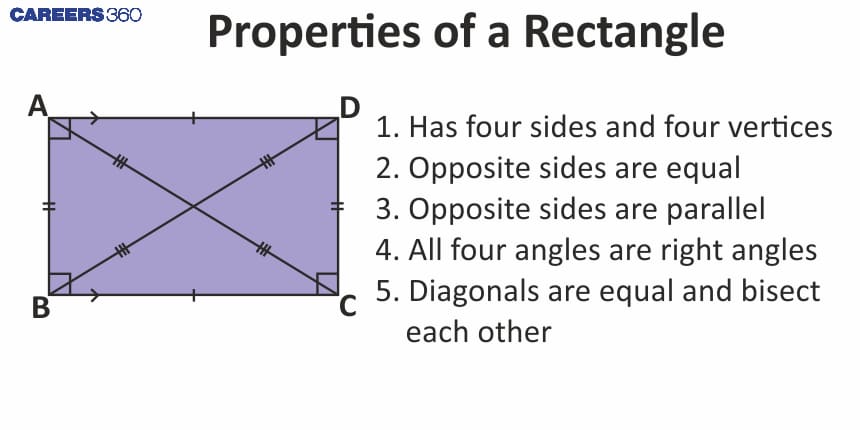
• Diagonals are equal in length.

• Diagonals bisect each other but do not necessarily bisect the angles.

• Opposite sides are parallel and equal.

Trapezium: A general description

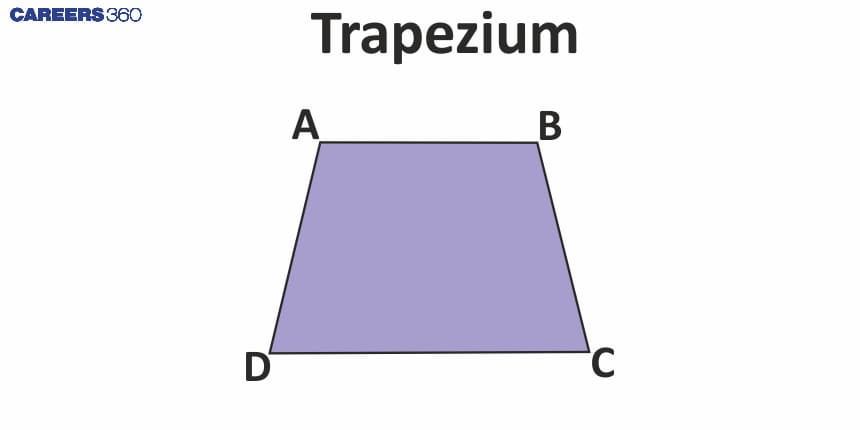
Sides and Angles of a Trapezium

• Has at least one pair of parallel sides (bases).

• Non-parallel sides are called legs.

• The angles between a base and a leg are supplementary.

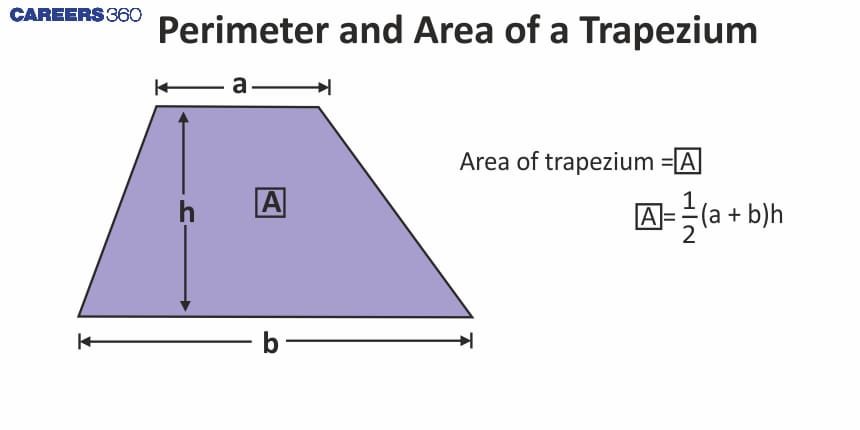
Perimeter and Area of a Trapezium

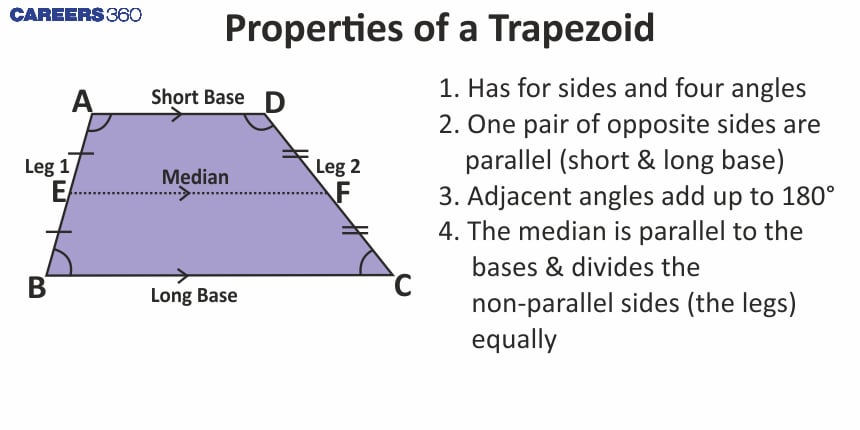
Important Properties of a trapezium

• The midsegment (median) is parallel to the bases and equal to half the sum of the bases.

• In an isosceles trapezium, the diagonals are equal.

Tips and Tricks

• Remember properties: Knowing each quadrilateral's basic properties helps solve problems quickly.

• Use symmetry: Many quadrilaterals have symmetrical properties (like squares and rhombuses), which can simplify calculations.

• Diagonals: For many quadrilaterals, properties related to diagonals (length, angle bisectors) are key to finding areas and other measurements.

• Visualization: Drawing the shapes and labeling known values can help in understanding the problem better.

Practice Questions/Solved Examples

Q.1.

The breadth of a rectangular floor is $\frac{3}{5}$ of its length. If the area of the floor is 60 m², then what is the difference between the length and breadth of the floor?

1. 6 m

2. 7.5 m

3. 4 m

4. 5 m

Hint: Area of rectangle = Length $\times$ Breadth

Solution:

Let the length of the rectangular hall be $5x$

⇒ Breadth of the rectangular hall $= 5x × \frac{3}{5} = 3x$

According to the question,

Area of the hall = 60 m$^2$

⇒ $3x × 5x = 60$

⇒ $15x^2 = 60$

⇒ $x^2 = 4$

⇒ $x = 2$

⇒ Difference between length and breadth $= 5x - 3x = 2x = 4$ m

Hence, the correct answer is 4 m.

Q.2.

Half of the perimeter of a rectangle is 30 cm. If the length of the rectangle is 6 cm more than its breadth, then what is the area of the rectangle (in cm2)?

1. 216

2. 250

3. 185

4. 150

Hint: The perimeter of a rectangle is given by P = 2l + 2w, where l is the length and w is the width. The area of a rectangle is given by A = l × w

Solution:

Half of the perimeter of a rectangle is 30 cm.

Let the length be $x$.

So, breadth = $x-6$

Total perimeter = 30 × 2

⇒ $2(x+x-6)=60$

⇒ $4x=72$

$\therefore x=18$

So, length = 18, breadth = 18 – 6 = 12

$\therefore$ Area of a rectangle = length × breadth = 18 × 12 = 216 cm2

Hence, the correct answer is 216 cm2.

Q.3.

The length of the diagonals of a rhombus is 40 cm and 60 cm. What is the length of the side of the rhombus?

1. $50 \sqrt{3} \ \text{cm}$

2. $20 \sqrt{3}\ \text{cm}$

3. $10 \sqrt{13}\ \text{cm}$

4. $40 \sqrt{13}\ \text{cm}$

Hint: In a rhombus, the diagonals are perpendicular bisectors of each other, and they divide the rhombus into four congruent right-angled triangles. Use this information to solve this problem.

Solution:

Let's denote the length of the side of the rhombus as $s$ and the diagonal as $d1$ and $d2$.

According to the given information, the diagonals of the rhombus are 40 cm and 60 cm.

These diagonals divide the rhombus into four congruent right-angled triangles.

Using the Pythagorean theorem, we can write the following equation for one of the right-angled triangles:

$(\frac{d1}{2})^2 + (\frac{d2}{2})^2 = (s)^2$

Simplifying this equation:

⇒ $(\frac{40}{2})^2 + (\frac{60}{2})^2 = (s)^2$

⇒ $(20)^2 + (30)^2 = (s)^2$

⇒ $s^2 = 1300$

⇒ $s = \sqrt{1300}$

⇒ $s = 10\sqrt{13}\ \text{cm}$

Hence, the correct answer is $10\sqrt13\ \text{cm}$.

Q.4.

What is the area of a rhombus whose diagonals are 8 cm and 13 cm?

1. 52 cm2

2. 96 cm2

3. 44 cm2

4. 84 cm2

Hint: We know, the area ($A$) of a Rhombus = $\frac{1}{2}d_1d_2$, where $d_1$ and $d_2$ are the length of two diagonals.

Solution:

Length of one diagonal ($d_1$) = 8 cm

Length of the other diagonal ($d_2$) = 13 cm

We know, the area ($A$) of a Rhombus = $\frac{1}{2}d_1d_2=\frac{1}{2}$× 8 × 13 = 52 cm2

Hence, the correct answer is 52 cm2.

Q.5.

The perimeter of a square is 124 metres. What is its area?

1. 448 m2

2. 884 m2

3. 764 m2

4. 961 m2

Hint: Perimeter of a square = 4 $\times$ Side

Area of a square = (Side)$^2$

Solution:

Given: The perimeter of a square is 124 metres.

Let the sides of the square be $a$.

So, 4$a$ = 124

⇒ $a$ = $\frac{124}{4}$ = 31

$\therefore$ Area = 312 = 961 m2

Hence, the correct answer is 961 m2.

Q.6.

The diagonal of the square is $8 \sqrt{2}$ cm. Find the diagonal of another square whose area is triple that of the first square.

1. $8 \sqrt{5}$ cm

2. $8 \sqrt{3}$ cm

3. $8 \sqrt{2}$ cm

4. $8 \sqrt{6}$ cm

Hint: Area of a square = (Side)$^2$

Diagonal of a square = $\frac{\text{Side}}{\sqrt{2}}$

Solution:

Given, Diagonal = $8\sqrt2$

$\therefore$ Side = $\frac{8\sqrt{2}}{\sqrt 2}=8$ cm

⇒ Area of this square = $(8)^2 = 64$ cm2

The Area of the Second square is triple the first one.

⇒ Area of the second one $= 64×3$

$\therefore$ Side of the 2nd square $= \sqrt{64×3} = 8\sqrt3$

⇒ The diagonal 2nd square $= \sqrt2×8\sqrt3 = 8\sqrt{6}$ cm

Hence, the correct answer is $8\sqrt6$ cm.

Q.7.

The ratio of the length of the parallel sides of a trapezium is $3:2$. The shortest distance between them is 15 cm. If the area of the trapezium is 450 cm$^2$ the sum of the length of the parallel sides is:

1. 15 cm

2. 36 cm

3. 42 cm

4. 60 cm

Hint: Use the formula: Area of trapezium = $\frac{1}{2}$ × (Sum of parallel sides) × height.

Solution:

Given: Height = 15 cm

Area of trapezium = 450 cm$^2$

Let the parallel sides be $3x$ and $2x$.

We know that,

Area of trapezium = $\frac{1}{2}$ × (Sum of parallel sides) × height

$450 = \frac{1}{2}×(3x+2x)×15$

⇒ $900 = 5x\ ×\ 15$

⇒ $x=12$

$\therefore$ The parallel sides are 3 × 12 = 36 and 2 × 12 = 24.

Sum of parallel sides = 36 + 24 = 60

Hence, the correct answer is 60 cm.

Q.8.

In the given figure, the area of isosceles triangle $\mathrm{ABE}$ is $72\;\mathrm{cm^2}$ and $\mathrm{BE = AB}$ and $\mathrm{AB = 2 AD}$, $\mathrm{AE \parallel DC}$, then what is the area (in$\;\mathrm{cm^2}$) of the trapezium $\mathrm{ABCD}$?

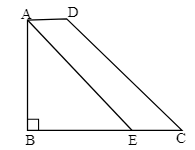
1. 108

2. 124

3. 136

4. 144

Hint: The area of trapezium $\mathrm{ABCD}$ $=\frac{1}{2} \times (\mathrm{sum\; of\; parallel\; sides}) \times \mathrm{height}$

Solution:

Given that the area of triangle $\mathrm{ABE}$ is $72\;\mathrm{cm^2}$.

The triangle is an isosceles.

$\mathrm{AB} = \mathrm{BE} = \sqrt{2 \times 72} = 12\;\mathrm{cm}$

$\mathrm{AB = 2 AD}$

⇒ $\mathrm{AD} = \frac{\mathrm{AB}}{2} = 6\;\mathrm{cm}$

Since $\mathrm{AE} \parallel \mathrm{DC}$

$\mathrm{CE} = \mathrm{AD} = 6\;\mathrm{cm}$, and $\mathrm{BC} = \mathrm{BE} + \mathrm{CE} = 12 + 6 = 18\;\mathrm{cm}$

The area of trapezium $\mathrm{ABCD}$ $=\frac{1}{2} \times (\mathrm{sum\; of\; parallel\; sides}) \times \mathrm{height} = \frac{1}{2} \times (18 + 6) \times 12 = 144\;\mathrm{cm^2}$

Hence, the correct answer is 144.

Q.9.

Parallel sides of a trapezium are $26\;\mathrm{cm}$ and $40\;\mathrm{cm}$ and the area is $792\;\mathrm{cm^2}$. What is the value of the distance (in $\mathrm{cm}$) between parallel sides?

1. 24 cm

2. 48 cm

3. 12 cm

4. 36 cm

Hint: The area of a trapezium $=\frac{1}{2} \times s\times d$

where $d$ and $s$ as the distance between parallel sides and the sum of parallel sides.

Solution:

Given that the parallel sides are $26\;\mathrm{cm}$ and $40\;\mathrm{cm}$, and the area is $792\;\mathrm{cm^2}$.

Let $d$ and $s$ as the distance between parallel sides and the sum of parallel sides.

The sum of parallel sides $=26+40 =66\;\mathrm{cm}$

The area of a trapezium $=\frac{1}{2} \times s\times d$

⇒ $792 = \frac{1}{2} \times 66 \times d$

⇒ $d = \frac{792 \times 2}{66} = 24\;\mathrm{cm}$

Hence, the correct answer is $24\;\mathrm{cm}$.

Q.10.

If the perimeter of a rhombus is 40 cm and one of its diagonals is 16 cm, what is the area (in cm2) of the rhombus?

1. 72

2. 48

3. 96

4. 192

Hint: The area of a rhombus $=\frac{1}{2} \times (\text{product of diagonals})$

Solution:

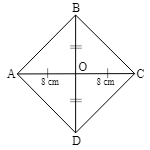
The perimeter of a rhombus is the sum of all its sides.

The side of rhombus $=\frac{40}{4} = 10\;\mathrm{cm}$

AB = BC = CD = DA = 10 cm

AC =16 cm

OA = OC = 8 cm

$\mathrm{OB} = \sqrt{(\mathrm{AB})^2 - (\mathrm{OA})^2} = \sqrt{(10)^2 - (8)^2} = \sqrt{36} = 6\;\mathrm{cm}$

⇒ BD = 6 × 2 = 12 cm

The area of a rhombus $=\frac{1}{2} \times (\mathrm{AC×BD})$

So, the area of the given rhombus $=\frac{1}{2} \times 16 \times 12 = 96\;\mathrm{cm^2}$

Hence, the correct answer is 96.