Similar Triangles: Definition, Properties, Formula, Theorem, Examples

Similar triangles are an important part of Geometry and Mathematics. Similar Triangles are triangles that have the same shape but may differ in size. They share key properties such as corresponding angles being equal and corresponding sides being proportional, known as the properties of the similar triangle. The similar triangles formula helps in calculating side lengths and areas, with properties of the area being proportional to the square of corresponding sides. Key similar triangle rules include the AA (Angle-Angle) criterion, SAS (Side-Angle-Side) criterion, and SSS (Side-Side-Side) criterion. The similar triangle symbol is $\sim$. The similar triangles theorems and similar triangles proofs are very important to establish these relationships. For practice, students can refer to similar triangles examples, similar triangles examples with answers, similar triangles example problems, and similar triangles worksheets. We will also discuss similar triangles' definitions and similar triangles' properties area in this article.

Similarity of two figures: Definition

In geometry, two figures are said to be similar if they have the same shape and characteristics but not necessarily the same size. So if we enlarge or shorten them and rotate or reflex, we can get the other figure.

Two figures can be similar if:

• All corresponding angles are equal.

• The ratios of the lengths of corresponding sides are equal (i.e., the sides are proportional).

Similarity is denoted by the symbol “~”.

If figure A is similar to figure B, then we can say that A ~ B.

Are two Circles always similar?

Yes, two circles are always similar as they are identical in shape.

Are two squares always similar?

Yes, All angles are equal and all sides are in proportion.

Similarity of two triangles

Two triangles are said to be similar if they have the same shape, but not necessarily the same size. This means that their corresponding angles are equal and their corresponding sides are in proportion. Also if we enlarge or shorten one triangle and rotate or reflex, we can get the other triangle.

Two triangles are similar if

• Corresponding angles are equal.

Example: $\angle$P = $\angle$Y, $\angle$Q = $\angle$X, $\angle$R = $\angle$Z

• Corresponding sides are proportional.

Example: PQ/XY = QR/XZ = PR/YZ

If triangle PQR is similar to triangle XYZ, then we can say that PQR ~ XYZ.

Criteria of Similarity of two triangles/ Similar triangle theorems

There are several criteria for two triangles to be similar. Those are:

• Angle-Angle(AA) Similarity Criterion

• Side-Angle-Side(SAS) Similarity Criterion

• Side-Side-Side(SSS) Similarity Criterion

Angle-Angle(AA) Similarity Criterion

Angle-Angle(AA) Similarity Criterion states that the triangles are similar if two angles of one triangle are equal to two angles of another triangle.

Suppose there are two triangles ABC and EFG.

Then ABC and EFG are similar triangles if any two pairs of angles between them are equal.

Let $\angle$A = $\angle$E and $\angle$B = $\angle$G

Then, $\triangle$ABC $\sim$ $\triangle$EGF

Side-Angle-Side(SAS) Similarity Criterion

Side-Angle-Side(SAS) Similarity Criterion states that if one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in proportion, the triangles are similar.

Suppose there are two triangles ABC and DEF.

Here, AB = DE
AC = DF

And, $\angle A = \angle D$

Then, $\triangle$ABC $\sim$ $\triangle$DEF

Side-Side-Side(SSS) Similarity Criterion

Side-Side-Side(SSS) Similarity Criterion states that if the corresponding sides of two triangles are in proportion, the triangles are similar.

Suppose there are two triangles ABC and DEF.

Then we can say ABC and DEF are similar triangles if their sides are in proportion.

Here, AB = DF = 9 cm, AC = DE = 6 cm, and BC = EF = 7 cm

Then, $\triangle$ABC $\sim$ $\triangle$DFE

Writing Similarity Statement:

The following steps are to be taken into consideration
Step 1: Determine the pairs of corresponding angles and pairs of corresponding sides in the triangles.

Step 2: Redraw the triangles following the orientation.
Step 3: Name the triangles and write a similarity statement, so that corresponding vertices are in the same order.

Example:

The triangles in the image below are similar. Write a similarity statement based on the image.

Step 1: Determine the pairs of corresponding angles and pairs of corresponding sides in the triangle.

Corresponding Angles:

∠??? = ∠???
∠??? = ∠???
∠??? = ∠???

Corresponding Sides:

?? and ??
?? and ??
?? and ??

Step 2: Redraw the triangles following their orientation.

Step 3: Name the triangles and write a similarity statement, so that the corresponding vertices are in the
same order.
$\Delta ABC \sim \Delta ECD$

What is CPST?

The full form of CPST is for “Corresponding Parts of Similar Triangles”. It is a concept in geometry that relates to the properties of similar triangles. When two triangles are similar, their corresponding parts (angles and sides) have specific relationships.

• In similar triangles, each pair of corresponding angles is equal.

• The lengths of corresponding sides of similar triangles are proportional.

CPST helps to solve problems involving similar triangles by using the relationships between corresponding parts.

Properties of Similar triangles

• Corresponding angles of similar triangles are equal.

If ABC ~ XYZ, then ∠A = ∠X, ∠B = ∠Y, and ∠C = ∠Z

• Corresponding sides of similar triangles are in proportion.

If ABC ~ XYZ, then AB/XY = BC/YZ = AC/XZ

• The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

If ABC ~ DEF, then $\frac{(\text{Area of} \ \triangle ABC)}{(\text{Area of} \ \triangle DEF)} = \frac{AB^2}{DE^2}$

• The ratio of the perimeters of two similar triangles is equal to the ratio of their corresponding sides.

If ABC ~ DEF, then $\frac{(\text{Perimeter of} \ \triangle ABC)}{(\text{Perimeter of} \ \triangle DEF)} = \frac{AB}{DE}$

• In similar triangles, the ratio of the corresponding altitudes, medians, and angle bisectors is equal to the ratio of the corresponding sides.

Comparison between Similar triangles and congruent triangles

Important notes on Similar triangles

• If two angles of one triangle are equal to two angles of another triangle, the triangles are similar.

• If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in proportion, the triangles are similar.

• If the corresponding sides of two triangles are in proportion, the triangles are similar.

• The ratio of areas of similar triangles equals the square of the ratio of sides of those similar triangles.

Practice Questions

Q1. The sides of two similar triangles are in the ratio 5 : 7. The areas of these triangles are in the ratio of:

1. 35 : 49

2. 15 : 49

3. 25 : 49

4. 36 : 49

Hint: For two similar triangles, the ratio of their areas is square of the ratio of their sides.

Answer:

The sides of two similar triangles are in the ratio of 5 : 7.

Let the sides be $5x$ and $7x$.

In two similar triangles, the ratio of their areas is square of the ratio of their sides.

$\frac{\textnormal{Area of triangle 1}}{\textnormal{Area of triangle 2}}=\frac{(\textnormal{Side of triangle 1})^2}{(\textnormal{Side of triangle 2})^2}$

$⇒\frac{\textnormal{Area of triangle 1}}{\textnormal{Area of triangle 2}}=\frac{({5x})^2}{({7x})^2}$

$\therefore\frac{\textnormal{Area of triangle 1}}{\textnormal{Area of triangle 2}}=\frac{25}{49}$

Hence, the correct answer is 25 : 49.

Q2. In the given $\triangle{ABC}, DE \parallel BC$. If $BC=8 \text{ cm}$, $DE=6 \text{ cm}$, and the area of $\triangle ADE=90 \text{ cm}^2$, what is the area of $\triangle ABC$?

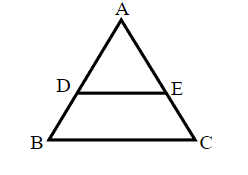
1. 140

2. 120

3. 160

4. 180

Hint: When two triangles are similar, the ratio of their areas is proportional to the square of the ratio of the respective sides. Using this concept, find the area of $(\triangle ABC)$.

Answer:

Given: $DE\parallel BC$ and $DE = 6\text{ cm}$, $BC = 8\text{ cm}$, and area of ($\triangle ADE) = 90 \text{ cm}^2$

Since $DE\parallel BC$, $\triangle ADE$ and $\triangle ABC$ are similar.

So, $\frac{(\text{Area of} \ \triangle ADE)}{(\text{Area of} \ \triangle ABC)} = \frac{DE^2}{BC^2}$

$⇒\frac{90}{(Area \ of \ \triangle ABC)} = \frac{6^2}{8^2}$

$⇒\frac{90}{Area\ of \ (\triangle ABC)}=\frac{36}{64}$

⇒ Area of $(\triangle ABC)=160 \text{ cm}^2$

Hence, the correct answer is 160.

Q3. Suppose $\triangle ABC$ be a right-angled triangle where $\angle A=90°$ and $AD\perp BC$. If the area of $\triangle ABC =40$ cm$^{2}$ and $\triangle ACD =10$ cm$^{2}$ and $\overline{AC}=9$ cm, then the length of $BC$ is:

1. 12 cm

2. 18 cm

3. 4 cm

4. 6 cm

Hint: In similar triangles, the ratio of their area is the square of the ratio of corresponding sides. Use this information to solve the question.

Answer:

According to the question,

Given: AC = 9 cm

Area of $\triangle$ABC = 40 cm2

Area of $\triangle$ADC = 10 cm2

$\triangle$BAC ∼ $\triangle$ADC

⇒ $\frac{\text{Area of }\triangle ABC}{\text{Area of } \triangle ADC}=\frac{AB^{2}}{AD^{2}}=\frac{BC^{2}}{AC^{2}}$

(In similar triangles, the ratio of their area is the square of the ratio of corresponding sides.)

⇒ $\frac{40}{10}=\frac{BC^{2}}{(9)^{2}}$

⇒ $\frac{40}{10}\times 81=BC^{2}$

⇒ $BC=18$ cm

Hence, the correct answer is 18 cm.

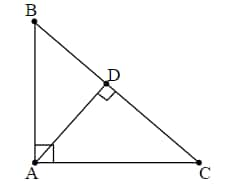
Q4. In the given figure, the triangle PQR is right-angled at Q. If PQ = 35 cm and QS = 28 cm and a semicircle passes from the point QRS, then what is the value (in cm) of SR?

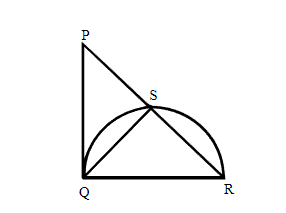
1. 35.33

2. 37.33

3. 41.33

4. 43.33

Hint: The angle made by the circle's diameter is a right angle.

Answer:

Given: Triangle PQR is right-angled at Q. If PQ = 35 cm and QS = 28 cm and a semicircle passes from the point QRS.

We know the angle made by the circle's diameter is a right angle.

So, $\angle$QSR = 90°

⇒ $\angle$PSQ = 90°

Now applying Pythagoras theorem in $\triangle$PSQ,

PS = $\sqrt{35^2-28^2}$

⇒ PS = 21 cm

Also, $\triangle$PSQ and $\triangle$QSR are similar triangles,

So, $\frac{PS}{QS}=\frac{QS}{SR}$

⇒ SR = $\frac{QS^2}{PS}$

⇒ SR = $\frac{28^2}{21}$

⇒ SR = $\frac{784}{21}$

⇒ SR = 37.33 cm

Hence, the correct answer is 37.33.

Q5. In $\triangle$ABC, D and E are points on AB and AC, respectively, such that DE || BC and DE divide the $\triangle$ABC into two parts of equal areas. The ratio of AD and BD is:

1. 1 : 1

2. $1:(\sqrt2-$1)

3. $1:\sqrt2$

4. $1:(\sqrt2+$1)

Hint: First, prove the similarity of triangles and then use the area of similar triangles theorem to solve the rest.

Answer:

Area($\triangle$ADE) = Area(trapezium BCED)

⇒ Area($\triangle$ADE) + Area($\triangle$ADE) = Area(trapezium BCED) + Area($\triangle$ADE)

⇒ 2 × Area($\triangle$ADE) = Area($\triangle$ABC)

In $\triangle$ADE and $\triangle$ABC,

$\angle$ADE = $\angle$ABC [i.e., corresponding angles in DE || BC]

$\angle$A = $\angle$A [common angle]

⇒ $\triangle$ADE ~ $\triangle$ABC

⇒ $\frac{\text{Area($\triangle$ADE)}}{\text{Area($\triangle$ABC)}}$ = $\frac{AD^2}{AB^2}$

⇒ $\frac{\text{Area($\triangle$ADE)}}{\text{2×Area($\triangle$ADE)}}$ = $\frac{AD^2}{AB^2}$

⇒ $\frac{1}{2}$ = $\frac{AD^2}{AB^2}$

⇒ $\frac{AD}{AB}$ = $\frac{1}{\sqrt2}$------------------(i)

⇒ AB = $\sqrt2$AD

⇒ AD + BD = $\sqrt2$AD

⇒ BD = $(\sqrt2-1)$AD

⇒ AD : BD = $1:(\sqrt2-1)$

Hence, the correct answer is $1:(\sqrt2-1)$.

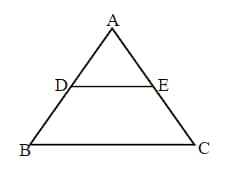
Q6. ABC is a triangle in which DE || BC and AD : DB = 5 : 4. Then DE : BC is:

1. 4 : 5

2. 5 : 9

3. 9 : 5

4. 5 : 7

Hint: Use the concept of similar triangles to solve this.

Answer:

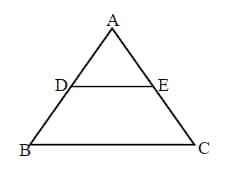
AD : DB = 5 : 4

In $\triangle$ADE and $\triangle$ABC,

$\angle$ADE = $\angle$ABC and $\angle$AED = $\angle$ACB [i.e., corresponding angles in DE || BC]

$\angle$A = $\angle$A [common angle]

⇒ $\triangle$ADE ~ $\triangle$ABC

⇒ $\frac{\text{AD}}{\text{AB}}$ = $\frac{\text{DE}}{\text{BC}}$

⇒ $\frac{5}{5+4}$ = $\frac{\text{DE}}{\text{BC}}$

⇒ $\frac{\text{DE}}{\text{BC}}$ = $\frac{5}{9}$

Hence, the correct answer is 5 : 9.

Q7. $\triangle$ABC is similar to $\triangle$PQR and AB : PQ = 2 : 3. AD is the median to the side BC in $\triangle$ABC and PS is the median to the side QR in $\triangle$PQR. What is the value of $(\frac{BD}{QS})^2$?

1. $\frac{3}{5}$

2. $\frac{4}{9}$

3. $\frac{2}{3}$

4. $\frac{4}{7}$

Hint: Use the concept of similar triangles to solve this.

Answer:

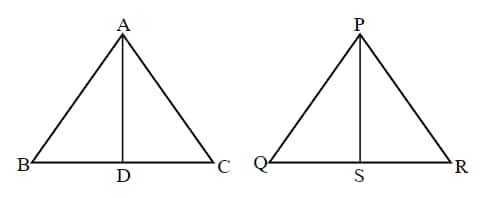
AB : PQ = 2 : 3

As $\triangle$ABC is similar to $\triangle$PQR,

$\frac{AB}{PQ}$ = $\frac{BC}{QR}$ = $\frac{CA}{RP}$ = $\frac{AD}{PS}$ = $\frac{BD}{QS}$ = $\frac{DC}{SR}$ = $\frac{2}{3}$

$(\frac{BD}{QS})^2$ = $(\frac{2}{3})^2$ = $\frac{4}{9}$

Hence, the correct answer is $\frac{4}{9}$.

Q8. Triangle ABC and DEF are similar. If AB = 92 cm, BC = 48 cm, AC =120 cm, and the length of the smallest side of triangle DEF is 200 cm, find the longest side of triangle DEF.

1. 400 cm

2. 225 cm

3. 350 cm

4. 500 cm

Hint: $\triangle ABC$ ~ $\triangle DEF$

⇒ $\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}$.

Answer:

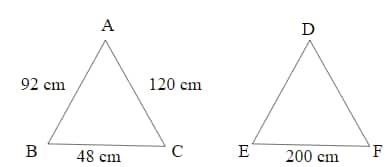
Given $\triangle$ABC ~ $\triangle$DEF,

⇒ $\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}$

⇒ $\frac{BC}{EF} = \frac{AC}{DF}$

⇒ $\frac{48}{200} = \frac{120}{DF}$

⇒ $DF = \frac{200 \times 120}{48}$

⇒ $DF = 500$ cm

So, the longest side of triangle DEF is 500 cm.

Hence, the correct answer is 500 cm.

Q9. If the ratio of corresponding sides of two similar triangles is $\sqrt{5}: \sqrt{7},$ then what is the ratio of the area of the two triangles?

1. $\sqrt[3]{5}: \sqrt{7}$

2. $25: 49$

3. $\sqrt{5}: \sqrt{7}$

4. $5: 7$

Hint: The ratio of areas of similar triangles is equal to the square of the ratio of sides of those similar triangles. Use this to solve the problem.

Answer:

Given, the ratio of sides of similar triangles = $\sqrt{5}: \sqrt{7}$

We know the ratio of areas of similar triangles equals the square of the ratio of sides of those similar triangles.

$\therefore$ Ratio of areas of similar triangles = $(\sqrt{5})^2: (\sqrt{7})^2=5 : 7$

Hence, the correct answer is $5 : 7$.

Q10. If $\triangle A B C \sim \triangle E D F$ such that $AB=6$ cm, $DF=16$ cm, and $DE=8$ cm, then the length of $BC$ is:

1. 12 cm

2. 10 cm

3. 14 cm

4. 8 cm

Hint: As $\triangle ABC \sim\triangle EDF$

⇒ $\frac{AB}{DE} = \frac{BC}{DF}$

Answer:

Given, $\triangle A B C \sim \triangle E D F$ such that $AB=6$ cm, $DF=16$ cm and $DE=8$ cm

As $\triangle ABC$ ~ $\triangle EDF$

⇒ $\frac{AB}{DE} = \frac{BC}{DF}$

⇒ $\frac{6}{8} = \frac{BC}{16}$

$\therefore BC= 12$ cm

Hence, the correct answer is 12 cm.