Sphere and Hemisphere: Definition, Formula, Difference, Questions

The sphere and hemisphere are important parts of 3d geometry or menstruation. A sphere is a 3 dimensional form of a circle and a hemisphere is nothing but half of the sphere. In this article, we will discuss ‘sphere and hemisphere formula’, ‘sphere and hemisphere difference’, ‘sphere and hemisphere diagram’, ‘sphere and hemisphere volume formula’, ‘sphere and hemisphere shape’, ‘sphere and hemisphere questions’ etc.

You will also find ‘sphere and hemisphere worksheet’, ‘sphere and hemisphere volume worksheet’ and you will need sphere and hemisphere volume formulas to solve the related questions.

Sphere and Hemisphere: An Overview

The sphere and hemisphere are some of the important topics in mensuration. A sphere has only one plane which is a curve plane. A hemisphere has one curved plane and one flat plane. Spheres are round in shape, and if we cut a sphere into two equal halves we will get two equal hemispheres.

Defining a Sphere

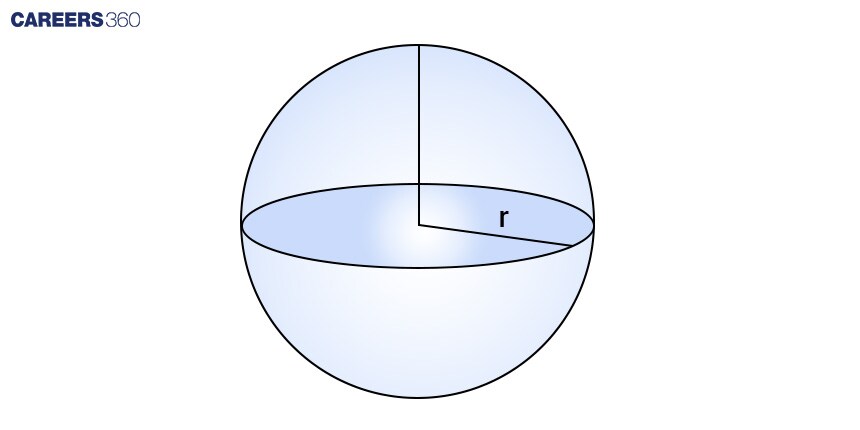
A sphere is defined as the set of all points in space that are equidistant from a fixed point, known as the centre. Some examples of a sphere include a basketball, a soap bubble, a tennis ball, etc. The important elements of a sphere are as follows:

Shape of a sphere

The shape of a sphere is round and it does not have any faces. The sphere is a geometrical three-dimensional solid having a curved surface. Like other solids, such as cubes, cuboids, cones, and cylinders, a sphere does not have any flat surface, a vertex, or an edge. Some real-life examples, which have a spherical shape are Basketball, a Globe, Marble, Orange etc.

Properties of a Sphere

The properties of a sphere are as follows:

• It is perfectly symmetrical in all directions.

• It has only a curved surface area.

• It is not a polyhedron as it has no edges, vertices, or flat faces.

• All the points on the surface of a sphere are equidistant from the center

• Among all the shapes with the same surface area, the sphere would have the largest volume.

Equation of a sphere

The equation of a sphere in three-dimensional Cartesian coordinates with the centre at $(h,k,l)$ and radius of $r$ is given as $(x-h)^2+(y-k)^2+(z-l)^2=r^2$

When the centre is at origin (0,0,0) the equation becomes $x^2+y^2+z^2=r^2$

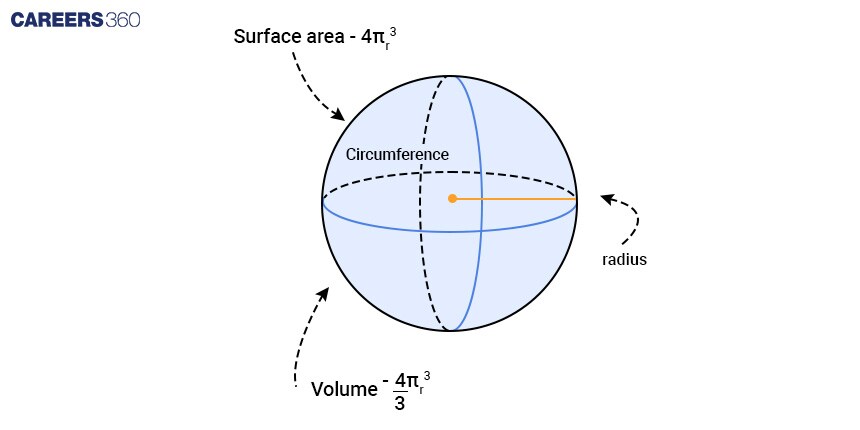
The surface area of a Sphere

The surface area of a sphere is the total area covered by the surface of a sphere in a three-dimensional space. It is measured in square units. The formula of surface area is given by: $4\pi r^2$, where $r$ is the radius of the sphere.

Volume of a Sphere?

The amount of space occupied by a sphere is called the volume of the sphere. It is measured in cubic units. The formula of volume is given by $\frac{4}{3}\pi r^3$, where $r$ is the radius of the sphere.

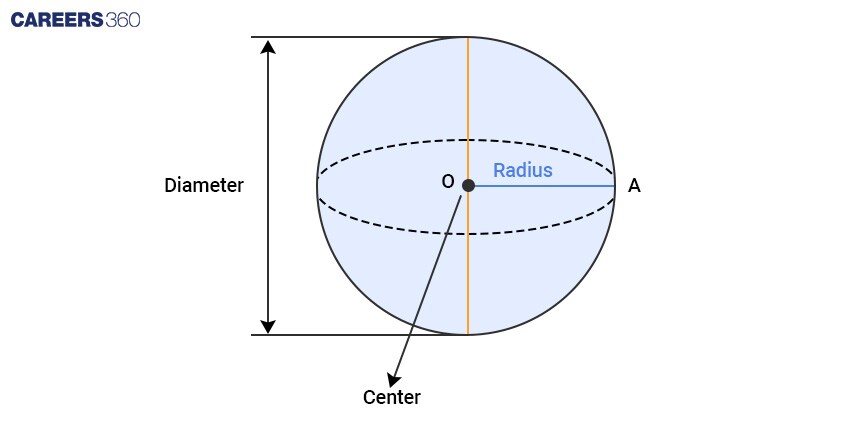
Difference between a sphere and a circle

What is a Hemisphere?

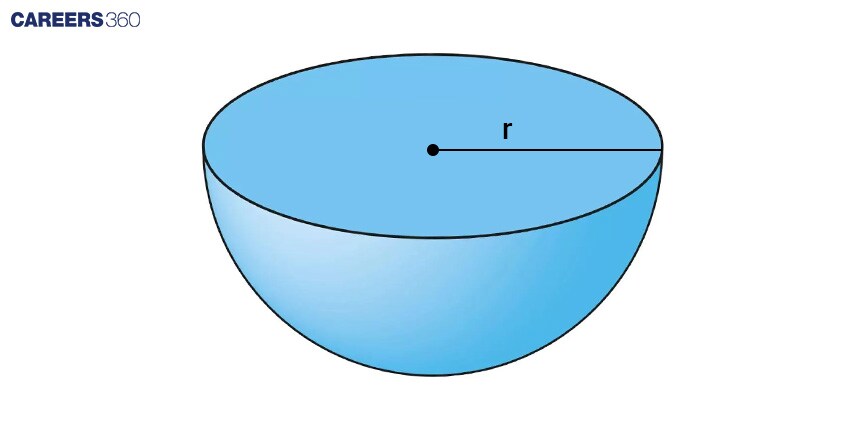
A hemisphere is half of a sphere, typically divided by a plane passing through the centre. It retains many properties of a sphere but is flat on one side.

Properties of a Hemisphere

The properties of a sphere are as follows:

• A hemisphere has a curved surface and a flat surface.

• Just like a sphere, there are no edges and no vertices in a hemisphere.

• A hemisphere is not a polyhedron since it has a circular base and one curved surface.

• The radius of the hemisphere is equal to the radius of the sphere.

Surface Area of a Hemisphere

The surface area of a hemisphere can be calculated by the area of its circular base along with its curved surface. The hemisphere can either be hollow or solid, according to that the surface area can be calculated. It is measured in square units and there are two types of surface area of a hemisphere.

Curved Surface Area of a Hemisphere

The curved surface of a hemisphere is considered the lateral area of a hemisphere and it can be calculated using the formula:

The curved surface area of a hemisphere = $2 \pi r^2$, where $r$ is the radius of the hemisphere.

The whole surface area of a Hemisphere

The whole surface area or the total surface area of a hemisphere is the sum of its curved surface area and the area of the circular base.

So, the whole surface area of a hemisphere = $2\pi r^2 + \pi r^2 = 3\pi r^2$, where $r$ is the radius of the hemisphere.

Volume of a Hemisphere

The volume of a hemisphere is the total capacity of the hemisphere and it is the number of cubic units covered inside that space. The volume of a hemisphere is calculated using the formula:

The volume of a hemisphere = $\frac{2}{3}\pi r^3$, where $r$ is the radius of the hemisphere.

Difference between Sphere and Hemisphere

List of Formulas:

Practice Questions/Solved Examples

Q.1.

Three solid metallic spheres of radii 1 cm, 6 cm, and 8 cm, respectively, are melted and recast into a single solid sphere. The radius of the new sphere formed is:

1. 9.0 cm

2. 5.9 cm

3. 7.7 cm

4. 8.5 cm

Hint: Use this formula: Volume of a sphere = $\frac{4}{3} \pi r^3$ (where $r$ is the radius)

Solution:

Given: The three original spheres had radii of 1 cm, 6 cm, and 8 cm, respectively.

Volume of a sphere $= \frac{4}{3} \pi r^3$ (where $r$ is the radius)

The total volume of the three original spheres

$=\frac{4}{3} \pi ×1^3 + \frac{4}{3} \pi × 6^3 + \frac{4}{3} \pi × 8^3$

$= \frac{4}{3} (\pi+216 \pi + 512 \pi)$

$= \frac{4}{3} × 729 \pi \ \text{cm}^3$

Let the radius of the new sphere formed be $R$ cm.

The volume of the new sphere = Sum of the volumes of the original spheres

⇒ $\frac{4}{3} \pi ×R^3 = \frac{4}{3} \pi × 729$

⇒ $R^3 = 729$

⇒ $R = 9$

So, the radius of the new sphere formed is 9.0 cm.

Hence, the correct answer is 9.0 cm.

Q.2.

If the inner radius of a hemispherical bowl is 5 cm and its thickness is 0.25 cm, find the volume of the material required to make the bowl. (Use $\pi = \frac{22}{7}$)

(Rounded up to two decimal places).

1. 34 cm3

2. 44 cm3

3. 45.34 cm3

4. 41.28 cm3

Hint: The formula to find the volume of a hemispherical bowl with inner radius $r$ and outer radius $R$ is $\frac{2}{3} × \pi × (R^{3} - r^{3})$.

Solution:

Volume of the hemispherical bowl = $\frac{2}{3} × \pi × (R^{3} - r^{3})$

Where, $r$ is the inner radius of the bowl = 5 cm

And, $R$ is the outer radius of the bowl = (5 + 0.25) = 5.25 cm

So, the volume $=\frac{2}{3} × \frac{22}{7} × [(5.25^{3}) - (5)^{3}]$

$=\frac{44}{21} × 19.70$

$= 41.28$ cm3

Hence, the correct answer is 41.28 cm3.

Q.3.

If the diameter of a sphere is 7 cm, find the volume of the sphere. (use $\pi=\frac{22}{7}$) (Rounded up to two decimal places).

1. $184 \ \text{cm}^3$

2. $201.34\ \text{cm}^3$

3. $128.87 \ \text{cm}^3$

4. $179.67 \ \text{cm}^3$

Hint: Volume of a sphere = $\frac{4}{3}\pi r^{3}$, where $r$ is the radius of the sphere.

Solution:

Given: The diameter of a sphere is 7 cm.

Volume of the sphere = $\frac{4}{3}\pi r^{3}$, where $r$ is the radius of the sphere.

Volume of the sphere $=\frac{4}{3}\pi (\frac{7}{2})^{3}=\frac{4}{3}×\frac{22}{7}×(\frac{7}{2})^{3} = 179.67 \ \text{cm}^3$

Hence, the correct answer is $179.67 \ \text{cm}^3$.

Q.4.

A ball is to be made with an inner radius of 2 units and an outside radius of 3 units. How much material is required to make the ball?

1. $\frac{19}{3} \pi$

2. $19 \pi$

3. $\frac{76}{3} \pi$

4. $\pi$

Hint: The volume of a spherical shell is $\frac{4}{3}\pi(R^{3} - r^{3})$, where the outer radius is $R$ and the inner radius is $r$.

Solution:

Given: Inner radius of 2 units and outside radius of 3 units.

The volume of a spherical shell is $\frac{4}{3}\pi(R^{3} - r^{3})$, where the outer radius is $R$ and the inner radius is $r$.

$=\frac{4}{3}\pi(3^{3} - 2^{3})$

$=\frac{4}{3}\pi(27-8)$

$=\frac{76}{3} \pi$

Hence, the correct answer is $\frac{76}{3} \pi$.

Q.5.

The radius of a sphere is doubled. The percentage increase in its surface area is ______.

1. 75%

2. 100%

3. 300%

4. 400%

Hint: Use the formula: The surface area of a sphere = $4\pi r^2$, where $r$ is the radius of the sphere.

Solution:

Let the radius of the sphere be $r$ units.

So, the surface area of the sphere = $4\pi r^2$ sq. units

After doubling, the new radius = 2$r$ units

So, the new surface area = $4\pi (2r)^2=16\pi r^2$ sq. units

$\therefore$ The percentage increase = $\frac{16\pi r^2-4\pi r^2}{4\pi r^2}×100=\frac{12\pi r^2}{4\pi r^2}×100= 300\%$

Hence, the correct answer is 300%.

Q.6.

The length of the largest possible rod that can be placed in a cubical room is $35\sqrt3$ metre. The surface area of the largest possible sphere that fits within the cubical room (assuming $\pi=\frac{22}{7}$) (in sq. metres) is:

1. 3500

2. 3850

3. 2450

4. 4250

Hint: Use the formula: The radius of the largest possible sphere that fits within a cubical room = $\frac{a}{2}$, where $a$ is the length of the sides of the cube.

Solution:

Given: The length of the largest possible rod that can be placed in a cubical room is $35\sqrt3$ metres.

The length of the largest rod = diagonal of the cube = side × $\sqrt3$

Here, side × $\sqrt3=35\sqrt3$

Or, the side of the cube = 35 metres

Now, the radius of the largest possible sphere that fits within the cubical room = $\frac{35}{2}$ metres

Therefore, the surface area of the sphere:

= $4\pi (\frac{35}{2})^2$

= $4×\frac{22}{7}×\frac{35}{2}×\frac{35}{2}$

= 3850 sq. metres

Hence, the correct answer is 3850.

Q.7.

What is the surface area (in cm²) of a spherical sculpture whose radius is 35 cm?

(Take $\pi=\frac{22}{7}$)

1. 16540

2. 15700

3. 15400

4. 14500

Hint: Use the formula: Surface area of sphere = $4\pi r^2$ where $r$ is the radius.

Solution:

The radius of spherical sculpture, $r$ = 35 cm

Surface area of sphere = $4\pi r^2$

= $4×\frac{22}{7}×{35}^2$

= 15400 cm2

Hence, the correct answer is 15400.

Q.8.

A hemispherical bowl has a radius of 7 cm. It is to be painted from inside as well as outside. Find the cost of painting it at the rate of Rs. 40 per 20 cm2. (Take the thickness of the bowl as negligible).

1. Rs. 1,232

2. Rs. 1,125

3. Rs. 1,432

4. Rs. 1,550

Hint: Use the formula: Curved surface area of hemisphere = $2\pi r^2$, where $r$ is the radius of the hemisphere.

Solution:

The radius of the hemispherical bowl = 7 cm.

Curved surface area = $2\pi r^2$

Inner and outer surface area of the bowl = $2×2\pi r^2$ = $4\pi r^2$

= $4×\frac{22}{7}×7×7$

= 616 cm2

Total cost of painting at the rate of Rs. 40 per 20 cm2

= $616 ×\frac{40}{20}$ = Rs. 1,232

Hence, the correct answer is Rs. 1,232.

Q.9.

The volume of a sphere of radius 4.2 cm is: (Use $\pi=\frac{22}{7}$)

1. 278.234 cm3

2. 312.725 cm3

3. 297.824 cm3

4. 310.464 cm3

Hint: The volume $V$ of a sphere with radius $r$ is

$V = \frac{4}{3} \pi r^3$

Solution:

The volume $V$ of a sphere with radius $r$ is

$V = \frac{4}{3} \pi r^3$

Putting $r = 4.2 \, \text{cm}$ and $\pi = \frac{22}{7}$.

$V = \frac{4}{3} \times \frac{22}{7} \times (4.2)^3=310.464 \, \text{cm}^3$

Hence, the correct answer is 310.464 cm3.

Q.10.

A spherical ball of lead, 3 cm in diameter, is melted and recast into three spherical balls. The diameters of two of these balls are $\frac{3}{2}$ cm and 2 cm, respectively. Find the diameter of the third ball.

1. 2.1 cm

2. 3.3 cm

3. 3 cm

4. 2.5 cm

Hint: The volume of the sphere is $\frac{4}{3}\pi r^3$ and the volume remains the same after recasting.

Solution:

Given:

A spherical ball of lead, 3 cm in diameter, is melted and recast into three spherical balls.

Radius = $\frac{3}{2}$ cm

So, the volume of the sphere = $\frac{4}{3}\pi r^3=\frac{4}{3}\pi (\frac{3}{2})^3$ cm3

The diameters of two of the new balls are $\frac{3}{2}$ cm and 2 cm, respectively.

Radii of these two balls are $\frac{\frac{3}{2}}{2},\frac{2}{2}$ respectively.

Let the radius of the third ball be $a$.

So, $\frac{4}{3}\pi (\frac{3}{2})^3=\frac{4}{3}\pi (\frac{\frac{3}{2}}{2})^3+\frac{4}{3}\pi(\frac{2}{2}^3)+\frac{4}{3}\pi a^3$

⇒ $\frac{4}{3}\pi (\frac{3}{2})^3=\frac{4}{3}\pi(\frac{27}{64}+1+a^3)$

⇒ $\frac{27}{8}=\frac{91}{64}+a^3$

⇒ $a^3=\frac{125}{64}$

⇒ $a=\frac{5}{4}$

So, the diameter of the third ball $= 2a=2×\frac{5}{4}=2.5$ cm

Hence, the correct answer is 2.5 cm.