Surface Area and Volume of a Pyramid: Formula, Calculator

The surface area and volume of a pyramid are one of the crucial topics in mensuration. The surface area of a pyramid is the region taken up by the surfaces of the pyramid and the volume of a pyramid is the total space occupied by the pyramid.

We will also discuss “surface area and volume of a square pyramid”, “surface area and volume of a hexagonal pyramid”, “surface area and volume of a rectangular pyramid”, and “surface area and volume of a triangular pyramid” in this chapter.

Also, you will find “surface area and volume of a pyramid worksheet’’, “surface area and volume of a pyramid formula”, “surface area and volume of a square pyramid”, and “surface area and volume of pyramids worksheet answers”in this article.

“surface area and volume of a pyramid calculator” and “surface area and volume of a triangular pyramid calculator” are used to find the surface area and volume ny directly placing the values of dimensions.

What is a Pyramid?

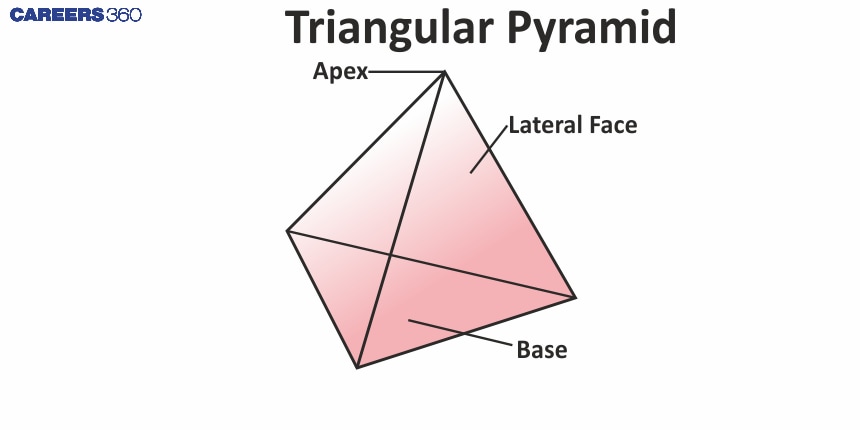
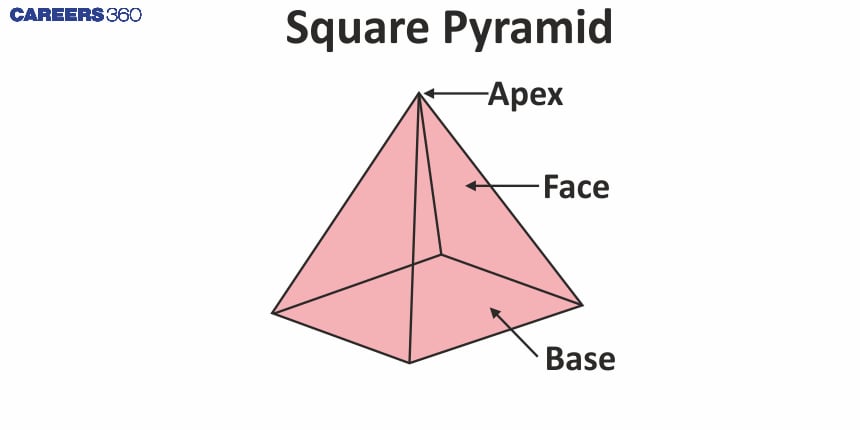
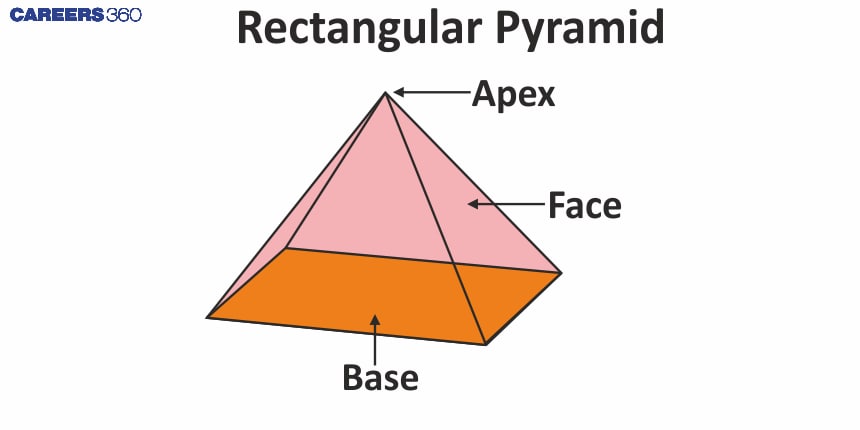
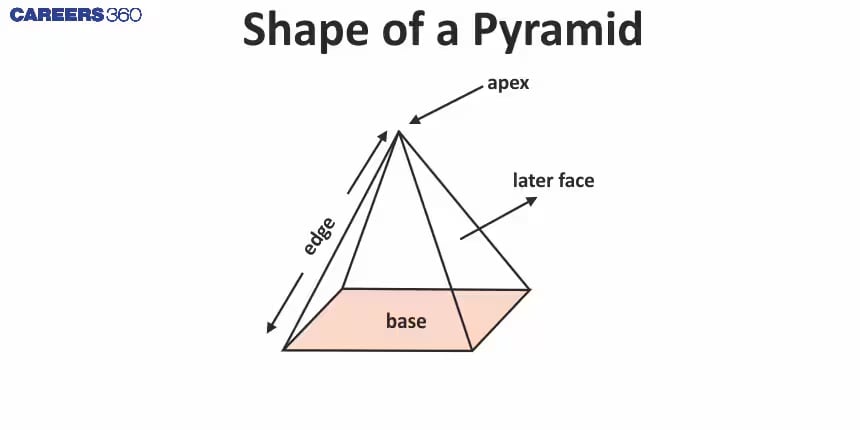
A pyramid is a three-dimensional shape with a polygonal base and triangular faces, which join at the apex or vertex.

The triangular faces are called lateral faces. The number of lateral faces equals the number of sides on its base.

All the triangular faces smoothly diverge to a common point at the top called the apex. Apex always stands opposite to the base.

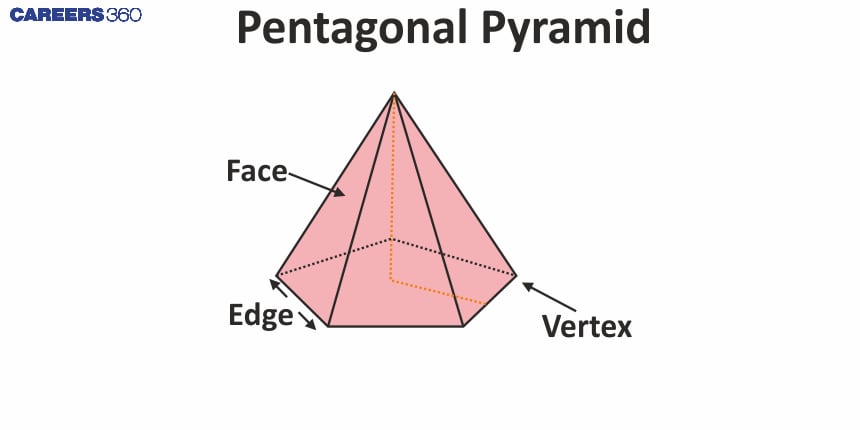
Edges of the pyramid are line segments formed by two intersecting faces.

Pyramids in real life are also made using this mechanism.

The picture below is the Pyramid of Giza in Egypt, one of the world's oldest and largest pyramids.

Properties of Pyramid

A Pyramid has some important properties which make it different from other three-dimensional geometrical shapes.

Some of its properties are:

• The base of a pyramid is a polygon like a triangle, square, or rectangle.

• The apex of a pyramid is the single point where all the triangular faces diverge and meet.

• All faces of a pyramid except the base are called lateral faces.

• A pyramid has only one base and several triangular faces which is equal to the number of sides of the base.

• A pyramid has vertices at the base corners and one at the apex.

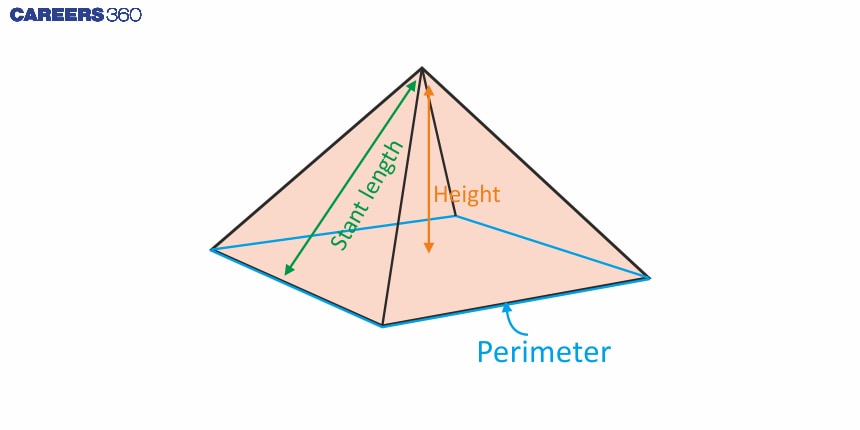
• The slant height of the pyramid is the distance from the apex to the midpoint of a base edge.

• Right pyramids with regular polygon bases are symmetric around their vertical axis.

Learning these properties is very important to differentiate Pyramid from other three-dimensional shapes.

Examples of Pyramid

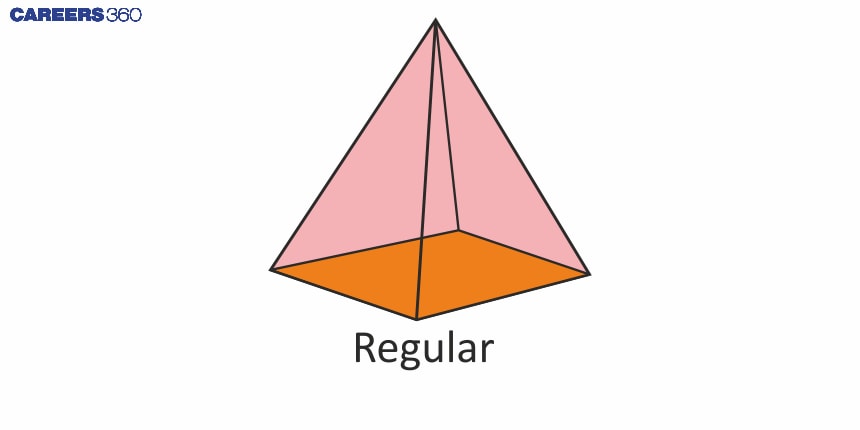
• Regular pyramid:

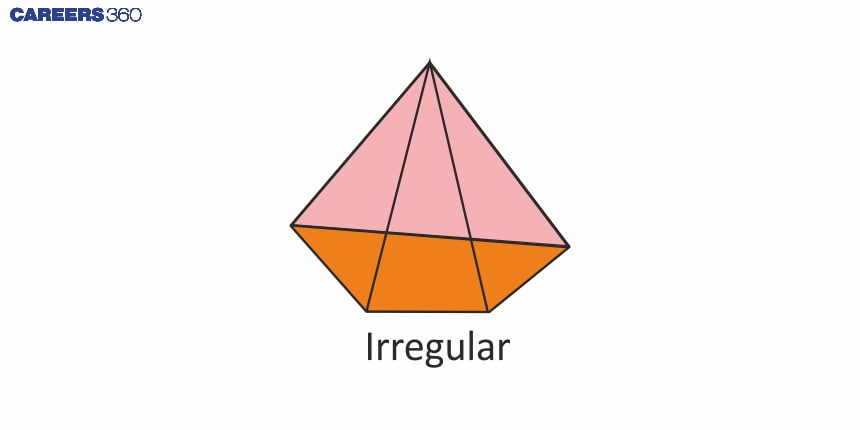
• Irregular pyramid:

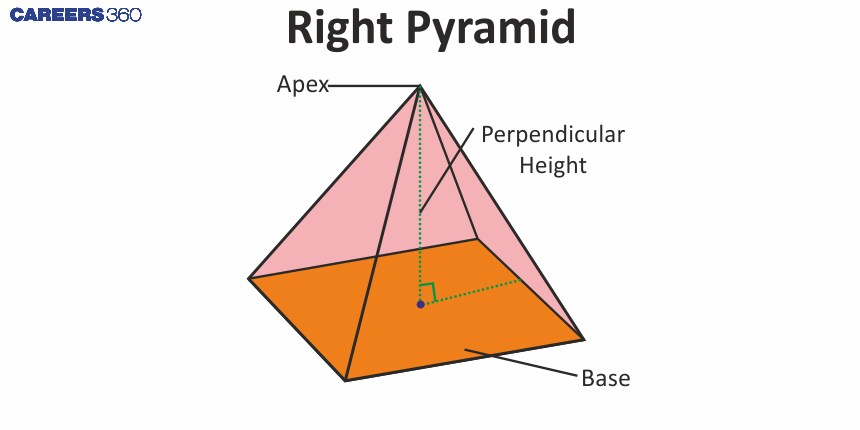
• Right pyramid:

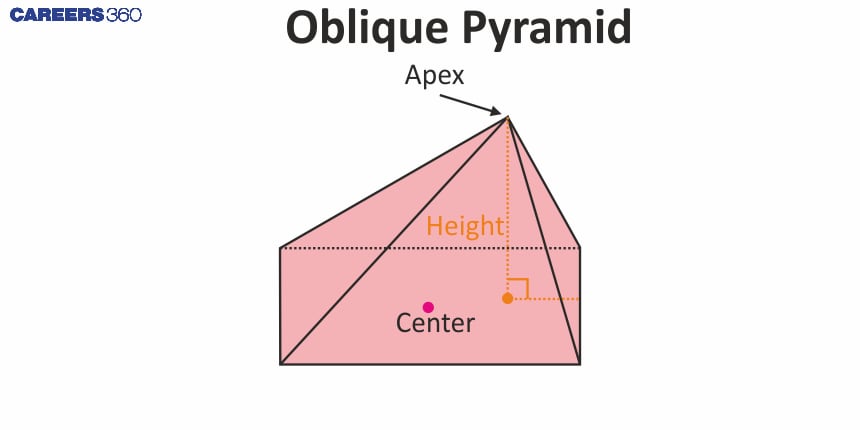
• Oblique pyramid:

Types of Pyramids based on the shape of the base

There are various types of Pyramids based on the shape of the base.

• Triangular pyramid

• Square pyramid

• Rectangular pyramid

• Pentagonal pyramid

• Hexagonal pyramid

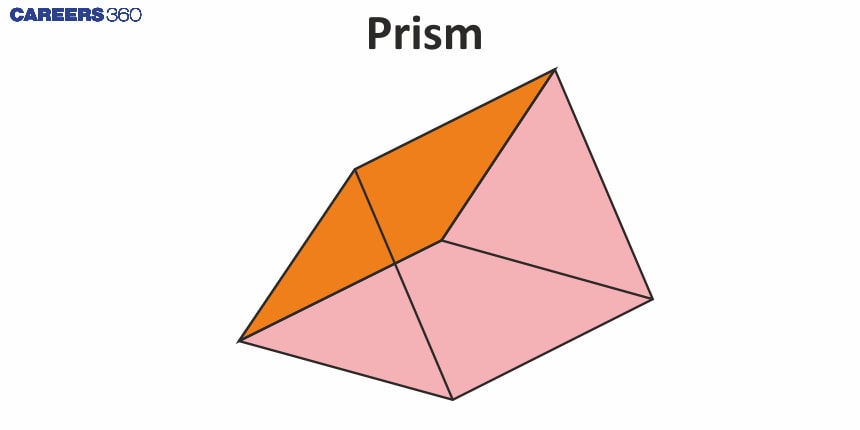
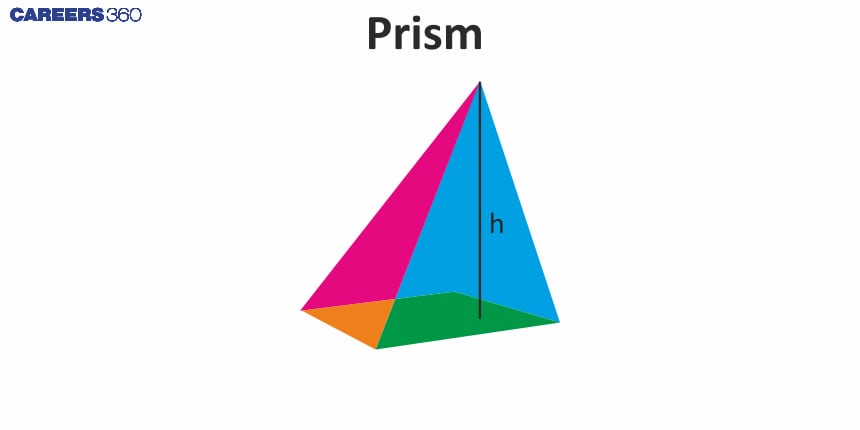
Difference between Prism and Pyramid

Prism and Pyramid both are three-dimensional polyhedrons with a polygon at their base.

But they have some differences.

Those are:

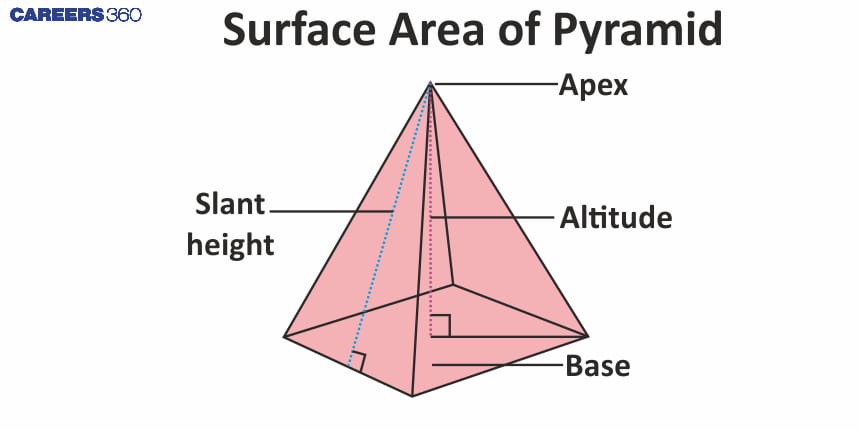
What is the Surface area of a Pyramid?

The surface area of a pyramid includes the base area and the lateral surface area of the pyramid.

There are different types of formulae to calculate the total surface area, lateral surface area, and base area of the pyramid.

Now we will discuss that.

The formula for the surface area of a Pyramid

Lateral Surface Area of a Pyramid

The lateral surface area of a pyramid is calculated by:

$\frac{1}{2}$ × Perimeter of base × Slant height

This formula changes whenever the shape of the base of a pyramid is changed.

Example:

A right pyramid stands on a base 16 cm square and its height is 15 cm. The area (in cm2) of its slant surface is:

Side of a square, $a$ = 16 cm

Height, $h$ = 15 cm

Perimeter $=4a=4\times 16=64$ cm

Slant height of the pyramid, $l=\sqrt{h^2+(\frac{a}{2}{)}^2}=\sqrt{{15}^2+8^2}=17$ cm

Lateral surface area = $\frac{1}{2}$ × Perimeter of base × Slant height

= $\frac{1}{2}\times 64\times 17$

= 544 cm2

Hence, the correct answer is 544.

Total Surface Area of a Pyramid

The base area of a pyramid will be the base area of the polygon.

There are two different types of formulae to calculate the total surface area of a pyramid.

• When the length of all the side faces is equal, the formula to find the total surface area is:

Base area + $\frac{1}{2}$ × Perimeter of the base × Slant height
Or
Base area + Lateral surface area

This formula changes whenever the shape of the base of a pyramid is changed.

Example:

What is the total surface area of a pyramid whose base is a square with a side 8 cm and the height of the pyramid is 3 cm?

Given,

The side of the square base = 8 cm and the height of the pyramid = 3 cm

The slant height (l) of the pyramid needs to be evaluated,

⇒ l2 = ($\frac{\text{side}}{2}$)2 + (Height)2

⇒ l2 = 42 + 32

⇒ l2 = 16 + 9

⇒ l2 = 25

⇒ l = 5 cm

The total surface area of the pyramid

= (Base Area) + $\frac{1}{2}$ × (Perimeter of base) × (Slant height)

= 64 + $\frac{1}{2}$ × 32 × 5

= 64 + 16 × 5

= 64 + 80

= 144 cm2

Hence, the correct answer is 144 cm2.

What is the Volume of a Pyramid?

The total area enclosed by a pyramid is called the volume of a pyramid. We measure the volume in cubic units.

Formula for the Volume of a Pyramid

The general formula to find the volume of a pyramid is:

$\frac{1}{3}$ × Base area × Height

This formula changes whenever the shape of the base of a pyramid is changed.

Example:

The base of a pyramid is an equilateral triangle of side 10 m. If the height of the pyramid is $40\sqrt{3}$ m, then the volume of the pyramid is:

The volume of the pyramid = $\frac{1}{3}\times (\text{The area of the base})\times (\text{Height})$,

The area of the equilateral triangle = $\frac{\sqrt{3}}{4}\times (\text{side}{)}^2=\frac{\sqrt{3}}{4}\times {10}^2=25\sqrt{3}$ m2

$\therefore$ The volume of the pyramid = $\frac{1}{3}\times 25\sqrt{3}\times 40\sqrt{3}=1000$ m3

List of Formulae

Note: The apothem (sometimes abbreviated as apo) of a regular polygon is a line segment from the center to the midpoint of one of its sides.

Important points

• Volume of a pyramid = $\frac{1}{3}$ × base area × height

• The volume of the prism = Base area × height

• The total surface area of a pyramid = Base area + 3 × The area of each triangular face

• Total surface area of the pyramid = (Base Area) + $\frac{1}{2}$ × (Perimeter of base) × (Slant height)

• Lateral surface area = $\frac{1}{2}$ × Perimeter of base × Slant height

• A regular triangular pyramid, also known as a tetrahedron, has four equilateral triangles as its faces.

Practice Questions

Q1. A prism and a pyramid have the same base and the same height. Find the ratio of the volumes of the prism and the pyramid.

1. 2 : 3

2. 3 : 1

3. 1 : 3

4. 3 : 2

Hint: Use the formulae:

The volume of the prism = Base area × height

Volume of pyramid = $\frac{1}{3}$ × base area × height

Answer:

The base area of the prism = Base area of the pyramid

Height of prism = Height of pyramid

Ratio of volumes of prism and pyramid

= (Base area × height) : ($\frac{1}{3}$ × base area × height)

= 3 : 1

Hence, the correct answer is 3 : 1.

Q2. A pyramid has an equilateral triangle as its base, of which each side is 8 cm. Its slant edge is 24 cm. The whole surface area of the pyramid (in cm2) is:

1. $(16\sqrt{3}+24\sqrt{35})$

2. $(12\sqrt{3}+24\sqrt{35})$

3. $(24\sqrt{3}+36\sqrt{35})$

4. $(16\sqrt{3}+48\sqrt{35})$

Hint: The total surface area of a pyramid = Base area + 3 × The area of each triangular face

Answer:

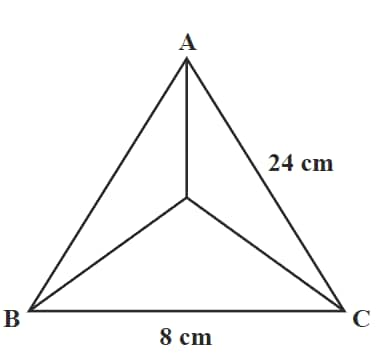
Total Surface area of a pyramid = Base area + 3 × The area of each triangular face

The area of a equilateral triangle with sides 8 cm = $\frac{\sqrt{3}}{4}\times (\text{side}{)}^2=\frac{\sqrt{3}}{4}\times 8^2=16\sqrt{3}{\text{cm}}^2$

Let the height of the pyramid be $h$.

$h^2={\text{Slant height}}^2-(\frac{1}{2}\times \text{base}{)}^2$

$\Rightarrow h^2={24}^2-(\frac{1}{2}\times 8{)}^2$

$h^2=576-16$

$\therefore h=\sqrt{560}=4\sqrt{35}\text{cm}$

The area of each triangular face = $\frac{1}{2}\times$ base × height = $\frac{1}{2}\times 8\times 4\sqrt{35}=16\sqrt{35}{\text{cm}}^2$

Total surface area of a pyramid = $16\sqrt{3}+3\times 16\sqrt{35}=(16\sqrt{3}+48\sqrt{35}){\text{cm}}^2$

Hence, the correct answer is $(16\sqrt{3}+48\sqrt{35}){\text{cm}}^2$.

Q3. A right pyramid stands on a square base of diagonal $10\sqrt{2}$ cm. If the height of the pyramid is 12 cm, the area (in cm2) of its slant surface is:

1. 520 cm2

2. 420 cm2

3. 360 cm2

4. 260 cm2

Hint: Use the formulas:

Area of the slant surface = $\frac{1}{2}\times p\times l$

Perimeter, $p$ = $4a$

Slant height, $l$ = $\sqrt{(\frac{a}{2}{)}^2+h^2}$

where $l$ = slant height, $h$ = height, $p$ = perimeter and $a$ = side of square base.

Answer:

Use the formulas:

Area of the slant surface = $\frac{1}{2}\times p\times l$

Perimeter, $p$ = $4a$

Slant height, $l$ = $\sqrt{(\frac{a}{2}{)}^2+h^2}$

where $l$ = slant height, $h$ = height, $p$ = perimeter and $a$ = side of square base.

Diagonal of square base $=10\sqrt{2}$ cm

Height of the pyramid, $h=12$ cm

Side of square base, $a=\frac{1}{\sqrt{2}}\times 10\sqrt{2}=10$ cm

Perimeter, $p=4a=4\times 10=40$ cm

Slant height, $l=\sqrt{(\frac{a}{2}{)}^2+h^2}=\sqrt{5^2+{12}^2}=\sqrt{169}=13$ cm

Area of the slant surface $=\frac{1}{2}\times 40\times 13=260$ cm2

Hence, the correct answer is 260 cm2.

Q4. The base of a right pyramid is an equilateral triangle of side $10\sqrt{3}$ cm. If the total surface area of the pyramid is $270\sqrt{3}$ sq. cm. its height is:

1. $12\sqrt{3}$ cm

2. 10 cm

3. $10\sqrt{3}$ cm

4. 12 cm

Hint: Total surface area of a pyramid $=\frac{1}{2}\times (\text{Perimeter of the base × Slant height) + Base area}$.

Answer:

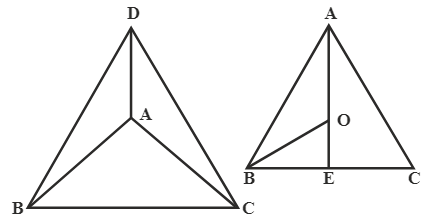
Given: The base of a right pyramid is an equilateral triangle.

Side of a triangle $AB=10\sqrt{3}$ cm

The total surface area of a pyramid $=270\sqrt{3}$ cm2

$\therefore$ Inradius of a triangle $OE=\frac{\text{side of equilateral triangle}}{2\sqrt{3}}$

= $\frac{10\sqrt{3}}{2\sqrt{3}}=5$ cm

Now, slant height (l) $=\sqrt{h^2+O{E}^2}$

$=\sqrt{h^2+25}$

Base area $=\frac{\sqrt{3}}{4}\times (10\sqrt{3}{)}^2$

Total surface area $=\frac{1}{2}\times (\text{perimeter of the base×slant height)+base area}$

⇒ $270\sqrt{3}=\frac{1}{2}(10\sqrt{3}\times 3\times \sqrt{h^2+25})+\frac{\sqrt{3}}{4}\times (10\sqrt{3}{)}^2$

⇒ $270\sqrt{3}=15\sqrt{3}(\sqrt{h^2+25})+75\sqrt{3}$

⇒ $15\sqrt{3}(\sqrt{h^2+25})=195\sqrt{3}$

⇒ $\sqrt{h^2+25}=13$

⇒ $h^2=144$

⇒ $h=12$ cm

Hence, the correct answer is $12$ cm.

Q5. The whole surface area of a pyramid whose base is a regular polygon is 340 cm2, the area of its base is 100 cm2, and the area of each lateral face is 30 cm2. Then the number of lateral faces is:

1. 8

2. 9

3. 7

4. 10

Hint: By finding the lateral surface area and dividing it by the area of each lateral face to get the solution.

Answer:

Given: Whole surface area = 340 cm2

Area of each lateral face = 30 cm2

Area of base = 100 cm2

Whole surface area = lateral surface area + area of the base

⇒ 340 = lateral surface area + 100

$\therefore$ Lateral surface area = 240 cm2

Thus, number of lateral faces = $\frac{240}{30}$ = 8

Hence, the correct answer is 8.

Q6. The base of a right pyramid is a square of side 10 cm. If the height of the pyramid is 12 cm, then its total surface area is:

1. 400 cm2

2. 460 cm2

3. 260 cm2

4. 360 cm2

Hint: By using the formula: Total surface area = lateral surface area + area of base.

Answer:

Given: Base = 10 cm

Height = 12 cm

$\therefore$ Slant height $=\sqrt{{\text{height}}^2+(\frac{\text{base}}{2}{)}^2}=\sqrt{{12}^2+5^2}$ = $\sqrt{144+25}=\sqrt{169}=13$ cm

Lateral surface area = $\frac{1}{2}$ × perimeter of base × slant height = $\frac{1}{2}$ × 40 × 13 = 260 cm2

Area of base = 10 × 10 = 100 cm2

$\therefore$ Total surface area = lateral surface area + area of the base = 260 + 100 = 360 cm2

Hence, the correct answer is 360 cm2.

Q7. The total surface area of a regular triangular pyramid with each edge of length 1 cm is:

1. $4\sqrt{3}$ cm2

2. $\frac{4}{3}\sqrt{3}$ cm2

3. $\sqrt{3}$ cm2

4. 4 cm2

Hint: The total surface area of a regular triangular pyramid is 4 times the area of an equilateral triangle.

Answer:

A regular triangular pyramid, also known as a tetrahedron, has four equilateral triangles as its faces.

The surface area of an equilateral triangle $=\frac{\sqrt{3}}{4}{a}^2$

Since a regular tetrahedron has four faces.

The total surface area is four times the surface area of one face $=4\times \frac{\sqrt{3}}{4}{a}^2=\sqrt{3}{a}^2$

Putting \(a = 1 \, \text{cm}\),

The total surface area of a regular triangular pyramid $=\sqrt{3}$ cm2

Hence, the correct answer is $\sqrt{3}$ cm2.