Important Theorem of Triangles: Definition, Pythagoras, Angle Bisector

Important theorems of triangles are one of the main foundations, in geometry. These theorems help us understand the properties of triangles in a better way and also provide useful insights about relationships between the sides and angles of triangles. Here we will explain what are the triangle theorems, how many triangle theorems are there, pythagoras theorem, pythagoras theorem formula, pythagoras theorem proof, pythagoras theorem questions, angle bisector theorem of triangle, angle bisector theorem proof, angle bisector theorem examples, Appolonius theorem, apollonius theorem formula, apollonius theorem proof etc.

Theorems of Triangle: An Overview

Theorems of Triangles are an important topic in geometry which plays a crucial role in establishing relationships with the sides and and angles of triangles. Given below is a list of important theorems associated with triangles, which we will discuss one by one with proper explanations.

List of Important Theorems

Explanation and Proof of some important theorems

Angle sum Property

The sum of the interior angles of a triangle is always 180 degrees.

Proof of Angle sum property:

Let’s draw a line PQ that passes through the vertex A and is parallel to side BC of the triangle ABC. We know that the sum of the angles on a straight line equals 180°.

In other words, ∠PAB + ∠BAC + ∠QAC = 180° ………..(1)

Now, since the line, PQ is parallel to BC,

∠PAB = ∠ABC and ∠QAC = ∠ACB. (Interior alternate angles)

Substituting these values in equation (1) we get,

∠ABC + ∠BAC + ∠ACB = 180°

Hence, the sum of the angles of a triangle is 180°. (proved)

Pythagoras theorem

In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Proof of Pythagoras theorem:

Consider a right-angled triangle ABC, right-angled at B. Draw a perpendicular BD meeting AC at D.

In △ABD and △ACB,

∠BAD = ∠BAC (common angle)

∠ADB = ∠ABC (both are right angle)

∠ABD = ∠ACB (remaining angle)

Thus, △ABD ∼ △ACB (by AAA similarity criterion)

Similarly, we can prove △BCD ∼ △ACB.

Now, △ABD ∼ △ACB, i.e. $\frac{AD}{AB}=\frac{AB}{AC}$.

⇒ AD × AC = AB2……….(1)

Similarly, △BCD ∼ △ACB, i.e. $\frac{CD}{BC}=\frac{BC}{AC}$.

⇒ CD × AC = BC2 ………….(2)

Adding these two equations, we get

AB2 + BC2 = (AD × AC) + (CD × AC)

⇒ AB2 + BC2 = AC(AD + DC)

⇒ AB2 + BC2 = AC2

Hence, the square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides. (proved)

Triangle inequality theorem

The sum of the lengths of any two sides of a triangle is greater than the length of the third side.

Proof of the Triangle inequality theorem:

Let ABC be a triangle; we need to prove that AB + AC > BC.

Extend BA to point D such that AD = AC, and join C to D.

We note that ∠ACD = ∠ADC, which means that in triangle BCD, ∠BCD > ∠BDC.

Sides opposite to larger angles are larger, i.e. BD > BC

⇒ AB + AD > BC

⇒ AB + AC > BC (as AD = AC)

Hence, the sum of the lengths of any two sides of a triangle is greater than the length of the third side. (proved)

Angle bisector theorem

The angle bisector of an angle of a triangle divides the opposite side into segments that are proportional to the other two sides.

Proof of Angle bisector theorem:

In triangle ABC, AD is the angle bisector of ∠BAC and we have to prove that $\frac{AB}{AC}=\frac{BD}{DC}$.

Draw CX parallel to AD and the extended BA intersects CX at E.

From the basic proportionality theorem, we know that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

In triangle CBE, DA is parallel to CE.

$\frac{BD}{DC}=\frac{BA}{AE}$ ……….. (1)

Now, we have to prove that AE = AC.

Since DA is parallel to CE, we have

∠DAB = ∠CEA (corresponding angles) ………. (2)

∠DAC = ∠ACE (alternate interior angles) ……….. (3)

Since AD is the bisector of ∠BAC, we have ∠DAB = ∠DAC ………. (4).

From (2), (3), and (4), we can say that ∠CEA = ∠ACE. It makes triangle ACE an isosceles triangle.

Since sides opposite to equal angles are equal, we have AC = AE.

Substitute AC for AE in equation (1),

$\frac{BD}{DC}=\frac{BA}{AC}$

⇒ $\frac{AB}{AC}=\frac{BD}{DC}$

Hence, The angle bisector of an angle of a triangle divides the opposite side into segments that are proportional to the other two sides. (proved)

Apollonius theorem

In any triangle, the sum of the squares of the lengths of any two sides is equal to twice the square of half the length of the third side plus twice the square of the median to the third side.

Proof of Apollonius theorem:

In the triangle PQR, O is the midpoint of QR, then we have to prove that PR² + PQ² = 2QO² + 2PO².

Let QR and OY be the x-axis and the y-axis as well as the coordinates of P, Q, and R be (b,c), (-a,0), and (a,0), respectively.

Now, PO² = (c – 0)² + (b – 0)² , (Since the coordinates of the point O are {0, 0})

⇒ PO² = c² + b²

Again PQ² = (c – 0)² + (b + a) ² = c² + (a + b)²

And QO² = (0 – 0)² + (- a – 0)² = a²

also, PR² = (c – 0) ² + (b – a) ² = c² + (a – b)²

Therefore, PR² + PQ² = c² + (a + b) ² + c² + (b – a)²

= 2c² + 2 (a² + b²)

= 2(b² + c²) + 2a²

= 2PO² + 2QO²

Hence, PR² + PQ² = 2QO² + 2PO². (Proved)

Midpoint theorem

the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the third side.

Proof of Midpoint theorem:

D and E are the midpoints of sides AB and AC in ΔABC.

We have to prove that, DE || BC and DE = $\frac{1}{2}$ × BC

In ΔABC, through C, draw a line parallel to BA, and extend DE such that it meets this parallel line at F.

From ΔAED with ΔCEF,

∠DAE = ∠ECF (alternate interior angles)

AE = EC (E is the midpoint of AC)

∠AED = ∠CEF (vertically opposite angles)

Therefore, ΔAED ≅ ΔCEF (ASA congruence)

So, DE = EF and AD = CF (Corresponding parts of congruent triangles are congruent)

Now, AD = BD

⇒ BD = CF

So, BCFD is a parallelogram. (Since BD || CF and BD = CF)

⇒ DF || BC and DF = BC

Therefore, DE || BC ……….(1)

Also, DE + EF = BC

⇒ 2DE = BC

⇒ DE = $\frac{1}{2}$ × BC ………….(2)

From (1) and (2) we get,

DE || BC and DE = $\frac{1}{2}$ × BC. (Proved)

Isosceles triangle theorem

In an isosceles triangle, the angles opposite the equal sides are equal.

Proof of Isosceles triangle theorem:

Let ∆ABC be an isosceles triangle with AB = AC.

Draw altitude AD from vertex A to the side BC.

We need to prove ∠ABC = ∠ACB

We know, that the altitude of an isosceles triangle from the vertex is the perpendicular bisector of the third side.

Thus, ∠ADB = ∠ADC = 90º and BD = DC ………….. (1)

From ∆ADB and ∆ADC,

AB = AC [Given]

AD = AD [Common side]

BD = DC [From equation (1)]

So, ∆ADB ≅ ∆ADC (SSS congruence)

Therefore, ∠ABC = ∠ACB (Corresponding parts of congruent triangles are congruent)

Hence, the angles opposite the equal sides are equal. (Proved)

Basic Proportionality theorem (BPT)

If a line is drawn parallel to one side of a triangle to intersect the other two sides, then it divides those sides in proportion.

Proof of Basic Proportionality theorem:

Let us have a triangle ABC and we draw a line LM parallel to side BC.

We have to prove that, $\frac{AL}{LB}=\frac{AM}{MC}$

First, draw a perpendicular LY on AM and another perpendicular MX on AL.

Now, join L, C and M, B.

We know, the area of a triangle = $\frac{1}{2}$ × Base × Height

Here, area of ΔALM = $\frac{1}{2}×AL×MX$

Area of ΔBLM = $\frac{1}{2}×LB×MX$

Also, area of ΔALM = $\frac{1}{2}×AM×LY$

Area of ΔCLM = $\frac{1}{2}×MC×LY$

Now, $\frac{Area of ΔALM}{Area of ΔBLM}=\frac{\frac{1}{2}×AL×MX}{\frac{1}{2}×LB×MX}$

⇒ $\frac{Area of ΔALM}{Area of ΔBLM}=\frac{AL}{LB}$ ………….(1)

Also, $\frac{Area of ΔALM}{Area of ΔCLM}=\frac{\frac{1}{2}×AM×LY}{\frac{1}{2}×MC×LY}$

⇒ $\frac{Area of ΔALM}{Area of ΔCLM}=\frac{AM}{MC}$ ………….(2)

According to the property of triangles, two triangles on the same base and between the same parallels are equal in area.

Therefore, ΔBLM and ΔCLM have equal areas.

So, from (1) and (2) we get,

$\frac{Area of ΔALM}{Area of ΔBLM}=\frac{Area of ΔALM}{Area of ΔCLM}$

⇒ $\frac{AL}{LB}=\frac{AM}{MC}$

Hence, If a line is drawn parallel to one side of a triangle to intersect the other two sides, then it divides those sides in proportion. (Proved)

Converse of BPT

If a line divides two sides of a triangle in the same ratio, then the line is parallel to the third side.

Proof of Converse of BPT:

Let us consider a triangle ABC with D and E two points on the side AB and AC such that $\frac{AD}{DB}=\frac{AE}{EC}$ ………..(1)

We have to prove that DE∥BC.

Let us draw a line DE’∥BC.

Now, as DE’∥BC in triangle ABC,

Thus, by using the Basic proportionality theorem,

$\frac{AD}{DB}=\frac{AE’}{E’C}$ ………….(2)

Using equations (1) and (2), we get

$\frac{AE}{EC}=\frac{AE’}{E’C}$

⇒ $\frac{AE}{EC}+1=\frac{AE’}{E’C}+1$ [Adding 1 to the both sides]

⇒ $\frac{AE+EC}{EC}=\frac{AE’+E’C}{E’C}$

⇒ $\frac{AC}{EC}=\frac{AC}{E’C}$

⇒ EC = E’C

This can only be possible if E and E’ are coincident.

Thus, E and E’ are the same points.

As, DE’∥BC

So, DE∥BC.

Hence, If a line divides two sides of a triangle in the same ratio, then the line is parallel to the third side. (Proved)

Stewart’s theorem

In any triangle, the sum of the squares of the lengths of the sides is equal to the sum of the square of the length of a median and the lengths of the two segments of the side divided by the median, adjusted by the length of the median.

Proof of Stewart’s theorem:

If $a, b, c$ are known to be the lengths of the triangle ABC. If $d$ is the length of the cevian of the side of the length $a$. Suppose this cevian divides the side $a$ into 2 segments of the length $m$ and $n$, where $m$ is adjacent to the side $c$ and whereas $n$ is adjacent to the side $b$, then we have to prove that - $b^m+c^n=a(d^2+mn)$

Consider $θ$ to be the angle between the side $m$ and side $d$. Let $θ$ be the angle between the side $n$ and side $d$. Also cos θ′ = (−cos θ).

Now, $c^2=m^2 + d^2 - 2.d.m.cos θ$.........(1) and $b^2=n^2 + d^2 - 2.d.n.cos θ’$

⇒ $b^2=n^2 + d^2 + 2.d.n.cos θ$ ………..(2) [As cos θ′ = (−cos θ)]

Multiply equation (1) with $n$ and equation (2) with $m$, then adding them we get,

$b^m+c^n=mn^2 + md^2 + 2dmn.cos θ + nm^2 + nd^2 - 2dmn.cos θ$

⇒ $b^m+c^n=mn^2 + nm^2 + md^2 + nd^2$

⇒ $b^m+c^n=mn(m+n) + d^2(m+n)$

⇒ $b^m+c^n=(m+n)(d^2+mn)$

⇒ $b^m+c^n=a(d^2+mn)$ (Proved).

Ceva’s theorem

For any triangle, lines drawn from each vertex to the opposite sides (or their extensions) are concurrent if and only if the product of the ratios of the divided sides is equal to 1.

Proof of Ceva’s theorem:

Consider a triangle ABC. Let CE, BG and AF be cevians that form a concurrent point at D.

We have to prove that $\frac{AG}{GC}×\frac{CF}{FB}×\frac{BE}{EA}=1$.

Let the area of the triangle be denoted using closed square brackets such as [ABG], [BGC], and so on.

Now, $\frac{AG}{GC}=\frac{[ADG]}{[CDG]}$

Also, $\frac{AG}{GC}=\frac{[ABG]}{[CBG]}$

⇒ $\frac{AG}{GC}=\frac{[ABG]}{[CBG]}=\frac{[ADG]}{[CDG]}$

⇒ $\frac{AG}{GC}=\frac{[ABG]-[ADG]}{[CBG]-[CDG]}$

⇒ $\frac{AG}{GC}=\frac{[ABD]}{[CBD]}$

Similarly, $\frac{CF}{FB}=\frac{[ADC]}{[ABD]}$ and $\frac{BE}{EA}=\frac{[CBD]}{[ADC]}$

Now, $\frac{AG}{GC}×\frac{CF}{FB}×\frac{BE}{EA}$

= $\frac{[ABD]}{[CBD]}×\frac{[ADC]}{[ABD]}×\frac{[CBD]}{[ADC]}$

= $1$

Hence, $\frac{AG}{GC}×\frac{CF}{FB}×\frac{BE}{EA}=1$ (Proved).

The inverse of Ceva’s theorem

If the product of the ratios of the divided sides is equal to 1, then lines drawn from each vertex to the opposite sides (or their extensions) of a triangle are concurrent.

Proof of the inverse of Ceva’s theorem

We have $\frac{AG}{GC}×\frac{CF}{FB}×\frac{BE}{EA}=1$.........(1)

We need to prove that CE, BG, and AF cevians are concurrent.

Let cevians CE and AF intersect at D and assume that the cevian passing through D is BH. So according to Ceva’s theorem,

$\frac{AH}{HC}×\frac{CF}{FB}×\frac{BE}{EA}=1$ ………….(2)

From (1) and (2),

$\frac{AG}{GC}×\frac{CF}{FB}×\frac{BE}{EA}=\frac{AH}{HC}×\frac{CF}{FB}×\frac{BE}{EA}$

⇒ $\frac{AG}{GC}=\frac{AH}{HC}$

It only holds true if G and H are the same point.

Hence, CE, BG, and AF cevians are concurrent. (Proved)

Important notes on theorems of triangles

• The angle sum property is fundamental in understanding triangle angles.

• Pythagoras' theorem is pivotal in right-angled triangle calculations.

• The exterior angle theorem aids in solving complex angle problems.

• The triangle inequality theorem is crucial in determining the feasibility of a triangle.

• Angle bisector and BPT are essential in similarity and proportionality problems.

• Ceva's and Stewart’s theorems are advanced concepts used in concurrency and cevian calculations.

Practice Questions/Solved Examples

Q.1.

In a right-angled triangle, if the hypotenuse is 20 cm and the ratio of the other two sides is 4 : 3, the lengths of the sides are:

1. 4 cm and 3 cm

2. 16 cm and 12 cm

3. 12 cm and 9 cm

4. 8 cm and 6 cm

Hint: Use the formula: (Hypotenuse)2 = (Perpendicular)2 + (Base)2

Solution:
Given: In a right-angled triangle, the hypotenuse is 20 cm and the ratio of the other two sides is 4 : 3.

Let the two sides be $4x$ cm and $3x$ cm.

Then $(4x)^2+(3x)^2=20^2$

⇒ $25x^2=400$

⇒ $x^2=\frac{400}{25}$

⇒ $x^2=16$

⇒ $x$ = 4

Therefore, the lengths of the two sides are (4 × 4) = 16 cm and (3 × 4) = 12 cm.

Hence, the correct answer is option (2).

Q.2.

$\triangle$ XYZ is a right-angled triangle and $\angle$Y = 90° If XY = 2.5 cm and YZ = 6 cm, then the circumradius of $\triangle$XYZ is:

1. 6.5 cm

2. 3.25 cm

3. 3 cm

4. 2.5 cm

Hint: The circumradius of a right-angled triangle is half of its hypotenuse.

Solution:

Given: XYZ is a right-angled triangle and $\angle$Y = 90°, where XY = 2.5 cm and YZ = 6 cm.

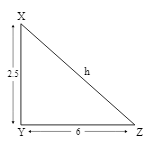
Let the hypotenuse of the triangle be $h$ cm.

So, $h^2=6^2+(2.5)^2$

⇒ $h=\sqrt{42.25}$

⇒ $h=6.5$ cm

We know,

The circumradius of a right-angled triangle is half of its hypotenuse.

So, the circumradius = $\frac{6.5}{2}$ = 3.25 cm

Hence, the correct answer is option (2).

Q.3.

Inside a square ABCD, $\triangle$BEC is an equilateral triangle. If CE and BD intersect at O, then $\angle$BOC is equal to:

1. 60°

2. 75°

3. 90°

4. 120°

Hint: The sum of the three angles of a triangle is 180°.

Solution:

Given: Inside a square ABCD, $\triangle$BEC is an equilateral triangle.

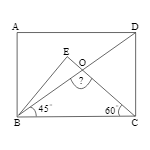
In $\triangle$BOC,

$\angle$BCO = 60° (angle of an equilateral triangle)

$\angle$OBC = $\frac{90°}{2}$ = 45° (as the diagonal of a square bisects its angle into two equal parts)

So, $\angle$BOC = 180° – (60° + 45°) = 75°

Hence, the correct answer is option (2).

Q.4.

Two medians AD and BE of $\triangle$ ABC intersect at G at right angles. If AD = 9 cm and BE = 6 cm, then the length of BD (in cm) is:

1. 10

2. 6

3. 5

4. 3

Hint: Here, the point of intersection of its medians, G divides the median in the ratio 2 : 1. Use Pythagoras theorem.

Solution:

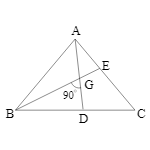
Given: AD = 9 cm

BE = 6 cm

$\angle$DGB = 90°

Here, the point of intersection of its medians, G divides the median in the ratio 2:1.

So, DG = $\frac{1}{3}×$AD = $\frac{1}{3}×9=3$ cm

BG = $\frac{2}{3}×$BE = $\frac{2}{3}×6=4$ cm

From Pythagoras theorem we know,

BD2 = DG2 + BG2

⇒ BD2 = $3^2+4^2=25$

$\therefore$ BD = $\sqrt{25}=5$ cm.

Hence, the correct answer is option (3).

Q.5.

Select the correct statement about the properties of a triangle.

1. The sum of two sides may be equal to the third side.

2. The sum of two sides is always equal to the third side.

3. The sum of two sides is always greater than the third side.

4. The sum of two sides is always less than the third side.

Hint: In a triangle, the sum of two sides is always greater than the third side.

Solution:

In a triangle, the sum of two sides is always greater than the third.

Hence, the correct answer is option (3).

Q.6.

If $\mathrm{D}$ is the midpoint of $\mathrm{BC}$ in $\triangle \mathrm{ABC}$ and $\angle A=90^{\circ}$, then $AD=$ ______.

1. $\frac{\mathrm{BC}}{4}$

2. $2 \mathrm{BC}$

3. $\frac{\mathrm{BC}}{2}$

4. $\mathrm{BC}$

Hint: The median to the hypotenuse of a right-angled triangle is half of the hypotenuse.

Solution:

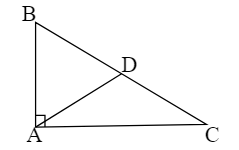
Given: In $\triangle \mathrm{ABC}$, the midpoint of $\mathrm{BC}$ is $\mathrm{D}$ and $\angle A=90^{\circ}$.

AD is the median to the BC.

We know that the median to the hypotenuse of a right-angled triangle is half of the hypotenuse.

$AD = \frac{1}{2} BC$

Hence, the correct answer is option (3).

Q.7.

The midpoints of AB and AC of a $\triangle ABC$ are X and Y, respectively. If BC + XY = 18 cm, then the value of BC – XY is:

1. 12 cm

2. 6 cm

3. 8 cm

4. 4 cm

Hint: The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.

Solution:

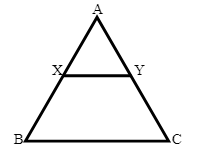
In $\triangle ABC$, $XY\parallel BC$ and $XY = \frac{1}{2}BC$.

Given: $BC + XY = 18$ cm

So, $BC + \frac{1}{2}BC = 18$

⇒ $BC = \frac{18}{1.5} = 12$

The length of $BC$ is 12 cm.

$BC - XY = BC - \frac{1}{2}BC = \frac{1}{2}BC$

⇒ $BC - XY = \frac{1}{2} \times 12 = 6$

Hence, the correct answer is option (2).

Q.8.

In a triangle DEF, DP is the bisector of $\angle D$, meeting EF at P. If DE = 14 cm, DF = 21 cm and EF = 9 cm, find EP.

1. 3.6 cm

2. 5.4 cm

3. 6.3 cm

4. 2.7 cm

Hint: By using the angle bisector theorem, states that the angle bisector of a triangle divides the opposite side into two parts that are proportional to the other two sides of the triangle.

Solution:

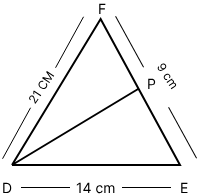
To find EP, we can use the angle bisector theorem, which states that the angle bisector of a triangle divides the opposite side into two parts that are proportional to the other two sides of the triangle.

Given: DE = 14 cm, DF = 21 cm and EF = 9 cm

DP is the bisector of $\angle D$

Now,

$\frac{EP}{PF} = \frac{DE}{DF}$

Substituting the given values, we get:

$\frac{EP}{9 - EP} = \frac{14}{21}$

⇒ 21 EP = 126 – 14 EP

⇒ 35 EP = 126

⇒ EP = $\frac{126}{35}$

⇒ EP = 3.6

Hence, the correct answer is option (1).

Q.9.

In $\triangle A B C$ the internal bisectors of $\angle ABC$ and $\angle ACB$ meet at $X$ and $\angle BAC=30^{\circ}$. The measure of $\angle BXC $ is:

1. $120^{\circ}$

2. $115^{\circ}$

3. $105^{\circ}$

4. $150^{\circ}$

Hint: Solve by using the concept of internal bisector angles of a triangle.

Solution:

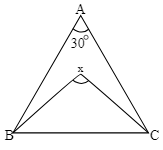
Given: $\angle \mathrm{BAC}=30^{\circ}$

We know that if the internal bisectors of $\angle ABC$ and $\angle ACB$ meet at $\mathrm{X}$ in $\triangle ABC$. Then,

$\angle BXC=90^{\circ}+\frac{1}{2}\angle BAC$

⇒ $\angle BXC=90^{\circ}+\frac{1}{2}×30^{\circ}$

⇒ $\angle BXC=105^{\circ}$

Hence, the correct answer is option (3).

Q.10.

If the two interior opposite angles of an exterior angle of a triangle are 35° and 65°, then the measurement of the exterior angle is:

1. 135°

2. 125°

3. 100°

4. 90°

Hint: An exterior angle is equal to the sum of two interior opposite angles of a triangle.

Solution:

Two interior opposite angles of a triangle are 35° and 65°.

Exterior angle = sum of two interior opposite angles = 35° + 65° = 100°

Hence, the correct answer is option (3).