Triangles and Congruence: Definition, Calculator, Questions, Formula

Triangles and congruence are fundamental parts of geometry, where we learn in which conditions two triangles are considered congruent. Here we will discuss what is congruency, the criteria of congruent triangles, the properties of congruent triangles, differences between similar and congruent triangles, triangles and congruence worksheet, triangles and congruence answer key, triangles congruence and similarity, triangles and congruence proofs, triangles and congruence quiz, triangles congruence statement, triangles congruence theorems, triangle congruence postulates, triangle congruence and proofs worksheet etc.

Triangles and Congruence: An Overview

Triangles are a type of geometric shape, which has three sides, three angles, and three vertices. Triangles can be classified into various forms depending on their sides and angles. Congruent triangles are those which have the same shape and same size, this property is called as congruency of triangles.

Meaning of Congruent

Two figures are said to be congruent if they have identical shape and size. In other words, one congruent figure can be superimposed onto the other through some transformations, such as translation, rotation, or reflection.

Congruent Triangles

Congruent triangles are triangles that have the same three sides and the same three angles. If two triangles are congruent, each pair of corresponding sides and each pair of corresponding angles are equal.

Criteria of Congruency of Two Triangles/ Triangle Congruence Theorem

There are specific criteria used to determine if two triangles are congruent:

• SSS (Side-Side-Side) Criterion: If all three sides of one triangle are equal to all three sides of another triangle, then the triangles are congruent.
  Here AB = QR
  BC = PR
  And AC = PQ. So, the two triangles are congruent.

• SAS (Side-Angle-Side) Criterion: If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
  Here AB = PQ
  BC = QR
  And included angles B and Q are equal.
  So, the two triangles are congruent.

• RHS (Right Angle-Hypotenuse-Side) Criterion: In right-angled triangles, if the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of another triangle, then the triangles are congruent.
  Here AB = PQ
  AC = PR
  And included angles B and Q are each equal to 90 degrees.
  So, the two triangles are congruent.

• AAS (Angle-Angle-Side) Criterion: If two angles and a non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
  Here, Angles A and P are equal
  Angles B and Q are equal
  BC = RQ
  AC = PR
  So, the two triangles are congruent.

• ASA (Angle-Side-Angle) Criterion: If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
  This criterion is not really required to be read separately as it was covered in the AAS criterion of congruency.

Writing congruence Statement:

When two triangles are congruent, we need to write a congruence statement. The order of the letters is very important, as corresponding parts must be written in the same order. If the letters are not written in the correct order then corresponding parts cannot be found perfectly.
Notice that the congruent sides also line up within the congruence statement.

Write a congruence statement for the two triangles below.

Here, $\angle T = \angle D$, RT = DF, and TS = DE
So, $\triangle RTS \cong \triangle FDE$
Why it is so?
Since $\angle T = \angle D$, T and D must be in front of each other.
TS = DE, and T and D are corresponding vertices. So, S and E must be written in front of each other.
The remaining two digits must be written correspondingly.

What is CPCT?

CPCT stands for "Corresponding Parts of Congruent Triangles." It is a principle that states that if two or more triangles are congruent, then all of their corresponding parts (sides and angles) are also congruent.

Properties of Congruent triangles

• Corresponding sides are equal.

• Corresponding angles are equal.

• The areas of congruent triangles are the same.

• The perimeters of congruent triangles are the same.

Difference between Similar triangles and congruent triangles

• Similar Triangles: Similar triangles have the same shape but not necessarily the same size. Their corresponding angles are equal, and their corresponding sides are proportional.

• Congruent Triangles: Congruent triangles have the same shape and size. All corresponding sides and angles are equal.

Tips and Tricks

• Always look for corresponding parts when trying to prove triangle congruence.

• Use congruence criteria (SSS, SAS, RHS, AAS) to identify congruent triangles quickly.

• Remember CPCT to deduce additional equal parts once triangles are proven congruent.

• Practice visualizing some transformations (translation, rotation, reflection) to understand congruence better.

Practice Questions/Solved Examples

Q.1.

In the given figure, $\Delta QPS \cong \Delta SRQ $. Find the measure of $\angle PSR$.

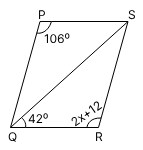
1. 64°

2. 74°

3. 52°

4. 82°

Hint: According to the properties of congruent triangles, two pairs of corresponding sides and the corresponding angles between them are equal.

Solution:

$\triangle$QPS = $\triangle$SRQ

$\angle$QPS = $\angle$SRQ (Congruent part of congruent triangles)

So, 106° = 2x + 12°

⇒ 106° – 12° = 2x

⇒ 94° = 2x

$\therefore$ x = 47°

$\angle$QPS = $\angle$SRQ = 106°

So, PQRS is a parallelogram.

$\angle$QSR = 180° – (42° + 106°) = 180° – 148° = 32°

$\angle$PQS = 32° (alternate interior angles)

$\angle$SQR =$\angle$PSQ = 42° (alternate interior angles)

$\therefore\angle$PSR = $\angle$QSR + $\angle$PSQ = 32° + 42° = 74°

Hence, the correct answer is option (2).

Q.2.

Which of the following statements is FALSE?

1. Two triangles are congruent if the size and shape of the triangles may or may not be equal.

2. SAS and SSS are both conditions of congruency of triangles.

3. If two angles and the included side of one triangle are equal to two angles and the included side of the other triangle, the triangles are congruent.

4. If two triangles are congruent, one of them can be superimposed on the other triangle.

Hint: We need both sizes and shapes to be equal for triangles to be congruent.

Solution:

Two triangles are congruent if they have the same shape and size.

In other words, the corresponding angles and sides of the two triangles are equal.

Congruent triangles are identical in shape and size.

So, the FALSE statement is ''Two triangles are congruent if the size and shape of the triangles may or may not be equal''.

Hence, the correct answer is option (1).

Q.3.

If $\triangle ABC$ and $\triangle DEF$ are congruent triangles, which of the following is FALSE?

1. The ratio of AC to DF is $2:1$

2. The perimeters of both the triangles are equal

3. AB = DE and BC = EF

4. The ratio of the angles in both the triangles is the same

Hint: When two triangles are found to be congruent, their corresponding sides and angles are also congruent.

Solution:

Given: $ \triangle ABC$ and $\triangle DEF$ are congruent triangles.

When two triangles are congruent, their corresponding sides and angles are also congruent.

Option 1: The ratio of AC to DF is $2:1$. This is incorrect.

Option 2: The perimeters of both triangles are equal. This is correct.

Option 3: AB = DE and BC = EF. This is correct.

Option 4: The ratio of the angles in both triangles is the same. This is correct.

Hence, the correct answer is option (1).

Q.4.

For congruent triangles $\triangle$ABC and $\triangle$DEF, which of the following statements is correct?

1. Perimeter of $\triangle \mathrm{ABC}=\frac{1}{2}$ Perimeter of $\triangle \mathrm{DEF}$

2. Perimeter of $\triangle \mathrm{ABC}=$ Perimeter of $\triangle \mathrm{DEF}$

3. Perimeter of $\triangle \mathrm{ABC}<$ Perimeter of $\triangle \mathrm{DEF}$

4. Perimeter of $\triangle \mathrm{ABC}>$ Perimeter of $\triangle \mathrm{DEF}$

Hint: The corresponding sides and angles of congruent triangles are equal.

Solution:

For congruent triangles $\triangle {ABC}$ and $\triangle {DEF}$,

$AB = DE$, $BC = EF$, $AC=DF$

So, $AB+BC+AC=DE+EF+DF$

So, perimeter of $\triangle \mathrm{ABC}=$ Perimeter of $\triangle \mathrm{DEF}$

Hence, the correct answer is option (2).

Q.5.

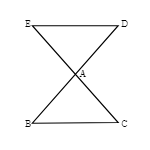
In the figure, AB = AD = 9 cm, AC = AE = 13 cm, and BC = 15 cm. Find ED.

1. 18 cm

2. 16 cm

3. 14 cm

4. 15 cm

Hint: $\triangle$ ABC congruents to $\triangle$ ADE by SAS, then BC = DE.

Solution:

Given: AB = AD = 9 cm, AC = AE = 13 cm, and BC = 15 cm.

$\triangle$ ABC congruent to $\triangle$ ADE by SAS

⇒ ED = BC = 15 cm

Hence, the correct answer is option (4).

Q.6.

If m$\angle$C = m$\angle$Z and AC = XZ, which of the following conditions is necessary for ΔABC and ΔXYZ to be congruent?

1. AB = AC

2. BC = YZ

3. AB = XY

4. BC = AB

Hint: SAS Congruency: If two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of another triangle, the triangles are congruent.

Solution:

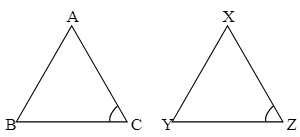
We have, m$\angle$C = m$\angle$Z and AC = XZ.

If BC = YZ, then by SAS congruency rule ΔABC and ΔXYZ are congruent.

Hence, the correct answer is option (2).

Q.7.

Let ABC and PQR be two congruent triangles such that $\angle $A = $\angle $P = $90^{\circ}$. If BC = 13 cm, PR = 5 cm, find AB.

1. 12 cm

2. 8 cm

3. 10 cm

4. 5 cm

Hint: By using Pythagoras' theorem: h2 = p2 + b2

Where h is the hypotenuse, p is the perpendicular, and b is the base.

Solution:

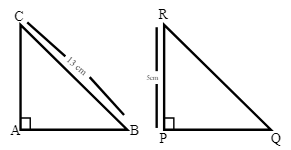
Given: $\triangle ABC$ and $\triangle PQR$

$\angle $A = $\angle $P = $90^{\circ}$

BC = 13 cm and PR = 5 cm

$\because$ Both the triangles are congruent

BC = QR and AC = PR

By using Pythagoras' theorem: h2 = p2 + b2

Where h is the hypotenuse, p is the perpendicular, and b is the base.

BC2 = AC2 + AB2

⇒132 = 52 + AB2

⇒ 169 – 25 = AB2

⇒ AB = 12

Hence, the correct answer is option (1).

Q.8.

If $\Delta \mathrm{XYZ} \cong \Delta \mathrm{LMR}$, then $m+x+p=?$

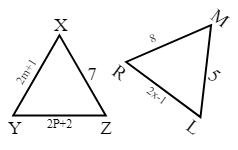
1. 7

2. 6

3. 9

4. 13

Hint: Congruent triangles have the same corresponding sides and angles.

Solution:

Given: $\Delta \mathrm{XYZ} \cong \Delta \mathrm{LMR}$

$\Delta \mathrm{XYZ}$ and $\Delta \mathrm{LMR}$ are congruent triangles.

We can say, $\mathrm{XY=LM}$

⇒ $2m+1=5$

⇒ $m=2$

$\mathrm{YZ=MR}$

⇒ $2p+2=8$

⇒ $p=3$

$\mathrm{ZX=RL}$

⇒ $2x–1=7$

⇒ $x=4$

So, $m+x+p=2+3+4$

⇒ $m+x+p=9$

Hence, the correct answer is option (3).

Q.9.

Two triangles XYZ and UVW are congruent. If the area of $\triangle$XYZ is 58 cm2, then the area of $\triangle$UVW will be:

1. 58 cm2

2. 116 cm2

3. 29 cm2

4. 15 cm2

Hint: The areas of two congruent triangles are equal.

Solution:

Two triangles XYZ and UVW are congruent.

The area of $\triangle$XYZ is 58 cm2.

We know,

The areas of two congruent triangles are equal.

Hence, the correct answer is option (1).

Q.10.

$\triangle$ LON and $\triangle$ LMN are two right-angled triangles with common hypotenuse LN such that $\angle$ LON = $90^{\circ}$ and $\angle$ LMN = $90^{\circ}$. LN is the bisector of $\angle$ OLM. If LN = 29 cm and ON = 20 cm, then what is the perimeter (in cm) of $\triangle$ LMN?

1. 67

2. 62

3. 65

4. 70

Hint: First, find the length of LO using Pythagoras theorem then prove that $\triangle$LON and $\triangle$LMN are congruent triangles. The perimeter of two congruent triangles is equal.

Solution:

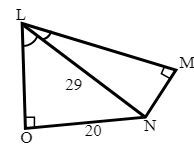
Given: $\triangle$LON and $\triangle$LMN are two right-angled triangles with common hypotenuse LN such that $\angle$LON = $90^{\circ}$ and $\angle$LMN = $90^{\circ}$. LN is the bisector of $\angle$OLM also, LN = 29 cm and ON = 20 cm.

In $\triangle$LON,

LO = $\sqrt{29^2-20^2}=\sqrt{441}$ = 21 cm

So, the perimeter of $\triangle$LON = 21 + 20 + 29 = 70 cm

Now, between $\triangle$LON and $\triangle$LMN,

$\angle$LON = $\angle$LMN, (right angle)

$\angle$OLN = $\angle$MLN, (since LN is the bisector of $\angle$OLM)

and LN = LN (general side)

So, $\triangle$LON and $\triangle$LMN are congruent triangles,

Therefore, the perimeter of $\triangle$LMN is also 70 cm.

Hence, the correct answer is option (4).