Types of Polynomials: Definition, Questions, Formula, Examples

Polynomials are algebraic expressions consisting of variables and coefficients, combined using addition, subtraction, and multiplication but not division. Understanding the types of polynomials is fundamental in algebra. There are different types of polynomials. If we explore the polynomial functions, the classification of polynomials can be based on their degree and the number of terms they contain. There are different types of polynomials based on degree like linear, quadratic, etc., based on the number of terms like monomial, binomial, etc.

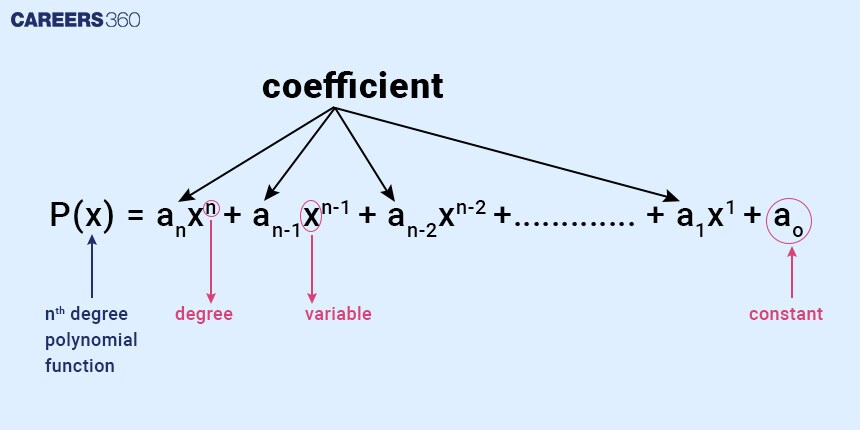
To answer the question “What is a polynomial?”, we can say that if an algebraic expression fits in the form of an xn + an-1 xn-1 + an-2 xn-2 + ........ + a1 x + a0, then it is a polynomial.

In this article, we will discuss questions like how many types of polynomials, different types of polynomials with examples and Polynomials types.

What is a Polynomial:

Polynomials are mathematical expressions that consist of variables or determinants, coefficients, exponents, and constant terms combined with mathematical expressions like addition, subtraction, or multiplication. Polynomials do not involve division by variables and have non-negative integer exponents.

Polynomials fit in the form of an xn + an-1 xn-1 + an-2 xn-2 + ........ + a1 x + a0.

Polynomial can be denoted by F(x), where x is the variable.

F(x) = 2x2 + 3x + 1

Variables can be changed.

If we denote the variable by y, then the function will be denoted by F(y).

F(y) = 2y2 + 3y + 1

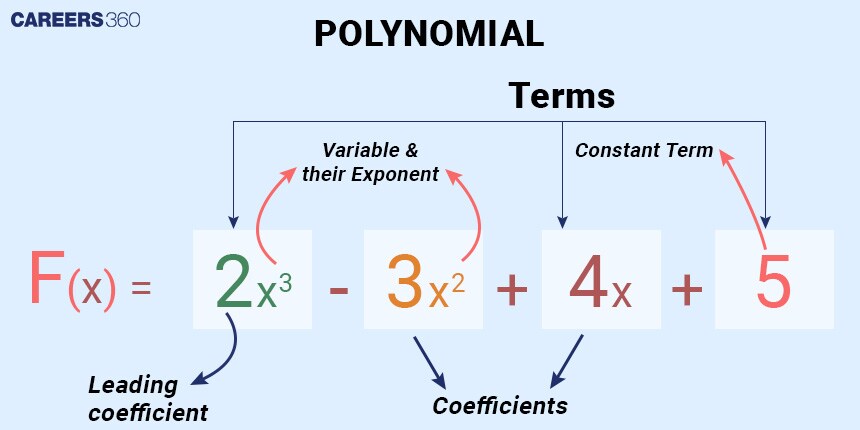
In the polynomial 7x2 + 3x + 1, 7 and 3 are coefficients of x2 and x, respectively. And 7 is the leading coefficient as it is in the front. 1 is the constant term. In 7x2, the power of x which is 2, is called exponent.

And variable of this polynomial is x.

Terms of a polynomial

The individual elements with which a polynomial is made are called Terms of a polynomial. Terms in the polynomial are separated by addition (+) or subtraction (-) sign.

In the polynomial x2 + 3x + 1, there are 3 terms, x2, 3x, and 1.

In the polynomial x2 + 2x, there are 2 terms, x2, and 2x.

In the polynomial 2x5, there is only 1 term, 2x5.

Degree of a Polynomial

The degree of a polynomial is the highest exponent of a variable in the polynomial expression with a non-zero coefficient.

The degree of the polynomial F(x) = x2 + 3x + x3 is 3, as the highest exponent of the variable is 3 in this polynomial.

The degree of the polynomial F(x) = x6 + x + 1 is 6, as the highest exponent of the variable is 6 in this polynomial.

The degree of the polynomial F(x) = 1 is 0, as the highest exponent of the constant term is 0 in this polynomial.

Types of Polynomial: Based on the degree of polynomial

Polynomials can be classified into four types based on the number of degrees of polynomials.

• Constant or Zero polynomial

• Linear polynomial

• Quadratic polynomial

• Cubic polynomial

• Biquadratic polynomial

Types of Polynomial: Based on the number of terms

Polynomials can be classified into three types based on the number of terms.

• Monomial

• Binomial

• Trinomial

Monomial

“Mono” means one. So, an algebraic expression with only one term can be called Monomial.

In that one term, there can be one or more than one variable.

Example:

Binomial

“Bi” means two. So, an algebraic expression with two terms can be called Monomial.

In those terms, there can be one or more than one variable.

Example:

Trinomial

“Tri” means three. So, an algebraic expression with three terms can be called a Trinomial.

In those terms, there can be one or more than one variable.

Example:

Special types of Polynomials

Apart from these conventional types of polynomials, there are some other types of polynomials which are shown below.

Properties of Polynomial

Polynomials have several important properties that distinguish them from other mathematical functions and expressions.
Some of the important properties of polynomials along with some important polynomial theorems are given below.

Property 1: Division Algorithm

Let f(x) be the dividend polynomial and g(x) be the divisor polynomial, where g(x) $\neq$ 0. Then there exists a unique quotient q(x) and remainder r(x) such that:

f(x) = g(x) × q(x) + r(x)

Where

• the degree of r(x) is less than g(x) when r(x) $\neq$ 0

or,

• r(x) will be a zero polynomial when f(x) is exactly divisible by g(x).

Property 2: Bezout’s Theorem

For two polynomials f(x) and g(x) with coefficients in the field of real or complex numbers, there exists polynomials a(x) and b(x), such that:

f(x) × a(x) + g(x) × b(x) = GCD of (f(x), g(x))

In general, it can be said that polynomials in the form of f(x) × a(x) + g(x) × b(x) are exactly multiple of the Greatest Common Divisor(GCD) of f(x) and g(x).

Property 3: Remainder Theorem

The remainder theorem states that:

If a polynomial f(x) is divided by (x - a), then the remainder will be f(a).

In simple words, it says that if we divide f(x) by (x - a), the remainder is the value of the polynomial evaluated at a.

Mathematically it can be written as

f(x) = (x - a) g(x) + f(a), where g(x) is the quotient of the polynomial

Property 4: Factor Theorem

Factor theorem states that:

When a polynomial f(x) is divided by (x - a), it will have no remainder if and only if (x - a) is a factor of the polynomial f(x).

In other words, if we divide a polynomial f(x) by (x - a), it will have no remainder if f(a) = 0

Property 5: Intermediate Value Theorem

Let f be a continuous function in a closed interval [a, b]. If two polynomials, f(a) $\neq$ f(b) and N is any number between f(a) and f(b), then there exists at least a number c ∈ (a, b) such that: f(c) = N

This property is crucial for solving polynomial equations and understanding the behavior of polynomials.

Property 6:

Algebraic functions like addition, subtraction, and multiplication of two polynomials result in a polynomial.

Let f(x) and g(x) be two polynomials.

Degree of (f(x) + g (x) is greater than or equal to the degree of f(x) or the degree of g(x).

Degree of (f(x) - g (x) is greater than or equal to the degree of f(x) or the degree of g(x).

Degree of (f(x) × g (x) = degree of f(x) + degree of g(x)

Property 7:

If a polynomial f(x) is divisible by a polynomial g(x), then every zero of g(x) is also a zero of f(x).

Zero of a polynomial which means a is called zero of f(x), if f(a) = 0

Mathematically this property can be written as

f(x) = g(x) × r(x) for some polynomial r(x).

Property 8:

If a polynomial f(x) is divisible by two co-prime polynomials g(x) and h(x), then it is divisible by the multiple of those two coprime polynomials.

Co-prime polynomials mean those two polynomials f(x) and g(x) have no other common factors other than their GCD(Greatest Common Divisor) 1.

Mathematically this property can be written as

f(x) = g(x) × h(x) where g(x) and h(x) are two co-prime polynomials

Property 9: Rule of Distinct Roots

Rule of Distinct roots states that a polynomial with degree n can have at most n distinct roots.

Let f(x) = f(x) = a0 + a1x + a2x2 + a3x3 + .......+ anxn be a polynomial such that deg(P) = n ≥ 0

Then, f(x) has at most n distinct roots.

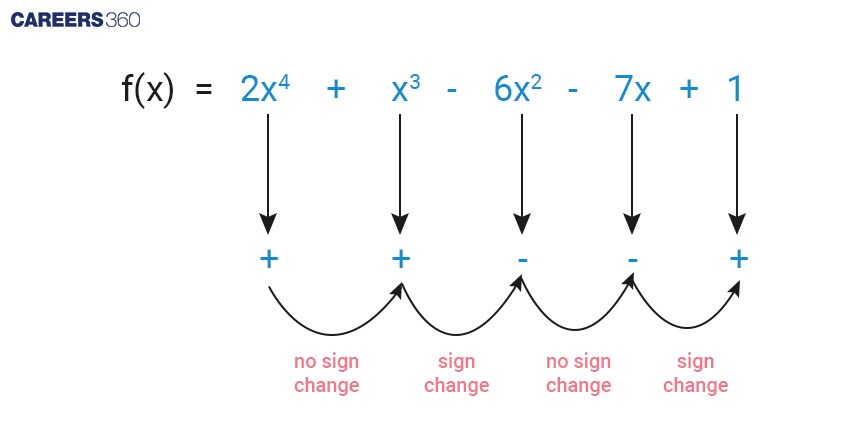
Property 10: Descartes’ Rule of Sign

The number of positive real roots of f(x) is the number of sign changes at most. Additionally, the actual number of positive real roots is either equal to the number of sign changes or is less than it by an even number.

The number of negative real roots of f(x) is at most the number of sign changes in f(-x). Similarly, the actual number of negative real roots is either equal to the number of sign changes or is less than it by an even number.

So, if there are “k” sign changes, the number of roots will be “k” or “(k – a)”, where “k” is some even number.

Example:

f(x) = 6x5 + 4x4 - 2x3 + x2 - x - 2

Here, the sign changes 3 times.

+4x4 → - 2x3

- 2x3 → + x2

+ x2 → - x

So, there will be 3 or 1(3 - 2) negative real solutions.

Property 11: Fundamental Theorem of Algebra

Every non-constant polynomial with complex coefficients has at least one complex root. This implies that the field of complex numbers is algebraically closed.

Mathematically it can be written as:

f(x) = an (x - r1) (x - r2) (x - r3)........(x - rn), where an is the leading coefficient and r1, r2, r3, ....., rn are roots which may be repeated or complex.

Property 12: Rule of Conjugate Roots

The Rule of Conjugate Roots states that for any polynomial with real coefficients if a complex number a + bi is a root, then its complex conjugate a – bi is also a root.

Consider a polynomial f(x) = an xn + an-1 xn-1 + an-2 xn-2 + ........ + a1 x + a0, where a0, a1, a2,...... an are real numbers. If a + bi is a complex root of f(x), then its conjugate root a - bi is also a root of f(x).

Polynomial Function and Equation

A polynomial function is a type of mathematical function that is defined by a polynomial.

A polynomial function f(x) with one variable x can be written as:

f(x) = an xn + an-1 xn-1 + an-2 xn-2 + ........ + a1 x + a0, where a0, a1, a2,...... an are coefficients (real numbers).

Example:

f(x) = 2x2 + 5x + 1 is a quadratic polynomial function.

f(x) = 8x3 + 3x + 1 is a cubic polynomial function.

f(x) = 2x + 3 is a linear polynomial function.

A polynomial equation equal to another polynomial function or a constant is called a Polynomial equation. Solving a polynomial equation involves finding the values of the variable that satisfy the equation.

It is generally written as f(x) = 0 for some polynomial f(x).

Example:

2x2 + 5x + 1 = 0 is a quadratic polynomial equation.

8x3 + 3x + 1 = 0 is a cubic polynomial equation.

2x + 3 = 0 is a linear polynomial equation.

Solving Polynomials

In many ways, a polynomial equation can be solved. First, we have to consider the equation equal to zero.

We have discussed below how to solve three types of polynomial equations.

• Linear equations

• Quadratic equations

• Cubic equations

Solving Linear Polynomial

A linear polynomial is a polynomial of degree 1.

Its general form is f(x) = ax + b

To solve it, we have to consider it equal to 0.

f(x) = 0

⇒ ax + b = 0

Then isolate the variable to solve it.

⇒ x = $-\frac{b}{a}$

Example:

Find the value of x in 5x - 20.

So, 5x - 20 = 0

⇒ 5x = 20

⇒ x = 4

Solving Quadratic Polynomial

A linear polynomial is a polynomial of degree 2.

Its general form is f(x) = ax2 + bx + c

To solve it, we have to consider it equal to 0.

f(x) = 0

⇒ ax2 + bx + c = 0

Then,

• Either we can split the midterm

Or,

• We can find the sum and product of the roots of the polynomial.

Mid-term split

x2 + 5x + 6

= x2 + 3x + 2x + 6

= x(x + 3) + 2 (x + 3)

= (x + 3) (x + 2)

Sum and product of the roots/Zeroes

For the quadratic equation ax2 + bx + c = 0 if the roots are α and β, then

Sum of the roots, α + β = $-\frac{b}{a}$

Product of the roots, α β = $\frac{c}{a}$

Example:

In x2 + 5x + 6, a = 1, b = 5, and c = 6

So, Sum of the roots = $-\frac{5}{1}$ = -5

And Product of the roots = $\frac{6}{1}$ = 6

If in a polynomial sum and product of the roots are given, then the polynomial can be written as:

f(x) = x2 – Sx + P, where S = sum of the roots and P = product of the roots

Solving Cubic Polynomial

A linear polynomial is a polynomial of degree 3.

Its general form is f(x) = ax3 + bx2 + cx + d

To solve it, we have to consider it equal to 0.

f(x) = 0

⇒ ax3 + bx2 + cx + d = 0

Then we can find the sum and product of the roots of the cubic polynomial.

Sum and product of the roots/Zeroes

For the cubic equation ax3 + bx2 + cx + d = 0, if the roots are α, β, and γ, then

Sum of the roots, α + β + γ = $-\frac{b}{a}$

Product of the roots, α β γ = $-\frac{d}{a}$

Sum of the product of roots taken two at a time, α β + β γ + α γ = $\frac{c}{a}$

Example:

6x3 + 2x2 + x + 1 is a cubic polynomial, where a = 6, b = 2, c = 1, d = 1

So, Sum of the roots = $-\frac{2}{6}=-\frac{1}{3}$

Product of the roots = $-\frac{1}{6}$

And the sum of the product of roots taken two at a time = $\frac{1}{6}$

Operations on Polynomial

There are four main types of polynomial operations.

1. Addition

2. Subtraction

3. Multiplication

4. Division

We will learn about each operation on polynomials with examples.

Addition

Addition of polynomials means adding the same type of terms or with the same powers of variables.

Addition of two or more polynomials gives us a polynomial as a result.

Example:

The sum of $6xy(2x-4z), 3yz(2x-3z)$ and $4xz(3y-2y^2)$ is:

$6xy(2x-4z)+ 3yz(2x-3z)$ + $4xz(3y-2y^2)$

= $12x^2y-24xyz+6xyz-9yz^2+12xyz-8xy^2z$

= $12x^2y-6xyz-9yz^2-8xy^2z$

Subtraction

Subtraction of polynomials means subtracting the same type of terms or with the same powers of variables.

Subtraction of two or more polynomials gives us a polynomial as a result.

Example:

If f(x) = 6x3 + 2x2 + 5 and g(x) = 4x3 + x2 - 5 , then find out f(x) - g(x).

So, f(x) - g(x) = (6x3 + 2x2 + 5) - (4x3 + x2 - 5) = 6x3 + 2x2 + 5 - 4x3 - x2 + 5 = 2x3 + x2 + 10

Multiplication

Multiplication of two polynomials means each term in the first polynomial is multiplied by each term in the second polynomial, and then the results are combined.

Multiplication of two or more polynomials gives us a polynomial as a result.

Example:

If f(x) = x + 2 and g(x) = y + 5, then find out f(x) × g (x).

So, f(x) × g (x) = xy + 2y + 5x + 10

Division

Polynomials can be divided by the long division method or synthetic division method.

Division of two or more polynomials does not necessarily give us a polynomial.

Example:

If f(x) = x2 - x - 6 and g(x) = x + 2, then find out f(x) / g (x).

If we midterm split f(x), then we get f(x) = (x + 2) (x - 3)

So, f(x) / g(x) = (x + 2) (x - 3)/ (x + 2) = x - 3

Tips and Tricks

• The standard form of a Linear polynomial is ax + b.

• The standard form of a Quadratic polynomial is ax2 + bx + c.

• The standard form of a Cubic polynomial is ax3 + bx2 + cx + d.

• The standard form of a biquadratic polynomial is ax4 + bx3 + cx2 + dx + e.

• Only add or subtract coefficients of terms with the same degree of polynomials.

• Multiplication of two polynomials means each term in the first polynomial is multiplied by each term in the second polynomial, and then the results are combined.

• For the quadratic equation ax2 + bx + c = 0 if the roots are α and β, then
  Sum of the roots, α + β = $-\frac{b}{a}$
  Product of the roots, α β = $\frac{c}{a}$

• For the cubic equation ax3 + bx2 + cx + d = 0, if the roots are α, β, and γ, then
  Sum of the roots, α + β + γ = $-\frac{b}{a}$
  Product of the roots, α β γ = $-\frac{d}{a}$
  Sum of the product of roots taken two at a time, α β + β γ + α γ = $\frac{c}{a}$

Practice Questions

Q1. If $x^{2}-3x+1=0$, then the value of ($x + \frac{1}{x}$) is:

1. 1

2. 0

3. 3

4. 2

Hint: First, move the $3x$ term to the right and then divide both sides by $x$.

Answer:

Given:

$x^{2}-3x+1=0$

⇒ $x^{2}+1=3x$

⇒ $\frac{x^{2} +1}{x}= 3$ (dividing both sides by $x$)

$\therefore x + \frac{1}{x} = 3$

Hence, the correct answer is 3.

Q2. What is the value of $64x^{3} + 36x^{2}y + 24xy^{2} + 2y^{3}$, when $x = 3$ and $y = -4?$

1. 304

2. 1456

3. 1584

4. 432

Hint: Make the equation in the form of $x^{2}(64x + 36y) + y^{2}(24x + 2y)$. Then, replace $x$ and $y$ with their given values.

Answer:

Given: $x = 3, y = -4$

So, the value of $64x^{3} + 36x^{2}y + 24xy^{2} + 2y^{3}$

$=x^{2}(64x + 36y) + y^{2}(24x + 2y)$

$=3^{2}[(64 × 3) + (36 × -4)] + (-4)^{2}[(24 × 3) + (2 × -4)]$

$=9 × [192 -144] + 16 × [72 -8]$

$=(9 × 48) + (16 × 64)$

$=432 + 1024$

$=1456$

Hence, the correct answer is $1456$.

Q3. If $x, y,$ and $z$ are the three factors of $a^3-7a-6$, then the value of $x+y+z$ will be:

1. 3a

2. 3

3. 6

4. a

Hint: Split $-7a$ into $(-a-6a)$ to get the factors $x,y,z$.

Answer:

Given:

$a^3-7a-6$

= $a^3-a-6a-6$

= $a(a^2-1)-6(a+1)$

= $a(a-1)(a+1)-6(a+1)$

= $(a+1)(a^2-a-6)$

= $(a+1)(a-3)(a+2)$

So, three factors x, y, z are $(a+1)(a-3)(a+2)$.

$\therefore x+y+z= (a+1)+(a-3)+(a+2)=3a$

Hence, the correct answer is $3a$.

Q4. If $(a+b)=5$, then the value of $(a-3)^7+(b-2)^7$ is:

1. $2^7$

2. $3^7$

3. 1

4. 0

Hint: Determine $a$'s value and substitute it into the provided expression to find the solution.

Answer:

Given: $(a+b)=5$

$⇒a=5-b$

The value of the expression $(a-3)^7+(b-2)^7$ is given as,

$=(5-b-3)^7+(b-2)^7$

$=(2-b)^7+(b-2)^7$

$=-(b-2)^7+(b-2)^7$

$=0$

Hence, the correct answer is $0$.

Q5. If $x^{4}+2x^{3}+ax^{2}+bx+9$ is a perfect square, where a and b are positive real numbers, then the value of $a$ and $b$ are:

1. $a=5, b=6$

2. $a=6, b=7$

3. $a=7, b=7$

4. $a=7, b=8$

Hint: Assume the equation to be $[(x-\alpha)(x-\beta)]^2$ where the roots are $\alpha$, $\alpha$, $\beta$, $\beta$. Now find $a$ and $b$ by taking the sum of two roots at a time and the sum of three roots at a time, respectively.

Answer:

Given:

$x^4+2x^3+ax^2+bx+9$

Solution:

$x^{4}+2x^{3}+ax^{2}+bx+9$

Let the equation be $[(x-\alpha)(x-\beta)]^2$

So the roots are $\alpha$, $\alpha$, $\beta$, $\beta$

$\alpha+\alpha+\beta+\beta=-2$ (Sum of roots = – coefficient of $x^3$ divided by coefficient of $x^4$)

$⇒\alpha+\beta=-1$

$\alpha \times \alpha \times \beta \times \beta=9$ (Product of roots = constant term divided by coefficient of $x^4$)

$⇒\alpha \times \beta=\pm 3$

The sum of two roots taken at a time = $a$ (sum of the roots taken two at a time = coefficient of $x^2$ divided by coefficient of $x^4$)

$a = \alpha^2+4\alpha\beta+\beta^2$

$⇒a = (\alpha+\beta)^2+2\alpha\beta$

$⇒a = 1 \pm 2 \times 3$

$⇒a = 1 + 6 = 7$ (Since, $a$ is positive $\alpha\beta=+3$)

The sum of three roots taken at a time = $-b$ (sum of the roots taken three at a time = – coefficient of $x$ divided by coefficient of $x^4$)

$-b = 2\alpha^2\beta+2\alpha\beta^2$

$⇒-b = 2\alpha\beta(\alpha+\beta)$

$⇒-b = 2\times -1\times 3$

$⇒-b = – 6$

$⇒b = 6$

Hence, the correct answer is '$a = 7$ and $b = 6$'.

Q6. If $a^3+3 a^2+3 a=63$, then the value of $a^2+2 a$ is:

1. 22

2. 19

3. 15

4. 8

Hint: Use the following information to solve this problem.

$(a+1)^3=a^3+3a^2+3a+1$

Answer:

$a^3+3 a^2+3 a=63$

We can factor the left side of the equation by recognizing it as a cube of a binomial,

$(a+1)^3=a^3+3a^2+3a+1$

Comparing this with the given equation, we have:

$(a+1)^3=63+1$

Taking the cube root of both sides, we get:

$a + 1 = \sqrt[3]{64}$

Simplifying further, we have:

$a + 1 = 4$

Subtracting 1 from both sides:

$a = 4 - 1$

⇒ $a = 3$

Now we can find the value of $a^2+2a$,

$a^2+2a = 3^2+2(3)=9+6=15$

$\therefore$ The value of $a^2+2a$ is 15

Hence, the correct answer is 15.

Q7. If $(x-2)$ is a factor of $x^2+3Qx - 2Q$, then the value of $Q$ is:

1. 2

2. -2

3. 1

4. -1

Hint: If $(x-2)$ is a factor of $P(x)$, then $P(2)=0$.

Answer:

Given: $(x-2)$ is a factor of $x^2+3Qx-2Q$.

Since $(x-2)$ is a factor of $P(x)=x^2+3Qx-2Q$.

Then, $P(2)=0$

So, $x^2+3Qx-2Q=0$

$⇒2^2+3Q\times2-2Q=0$

$⇒4+6Q-2Q=0$

$⇒4Q=-4$

$\therefore Q=-1$

Hence, the correct answer is –1.

Q8. If $x^{3}+2x^{2}-5x+k$ is divisible by $x+1$, then what is the value of $k$?

1. -6

2. -1

3. 0

4. 6

Hint: If $x - a$ is the factor of $p(x)$, then $p(a) = 0$.

Answer:

Given: $f(x)=x^3+2x^2-5x+k=0$ is divisible by $x+1$.

So, $ x^3+2x^2-5x+k=0$ when $x=-1$

⇒ $ (-1)^3+2(-1)^2-5(-1)+k=0$

⇒ $-1+2+5+k=0$

⇒ $ k = -6$

Hence, the correct answer is –6.

Q9. Which of the following equations has 7 as a root?

1. $3x^2-6x+2=0$

2. $x^2-9x+14=0$

3. $x^2-7x+10=0$

4. $x^2+3x-12=0$

Hint: Use middle-term splitting of expression to find its root.

Answer:

Given:

Option 1:

$3x^2-6x+2=0$

Using the quadratic formula, we get,

$⇒x=\frac{6\pm\sqrt{(-6)^2-4.3.2}}{2.3}$

So, $x=\frac{\sqrt3+3}{3}$ or $x=\frac{-\sqrt{3}+3}{3}$

So, the value of $x\neq7$.

Option 2:

$x^2-9x+14=0$

$⇒x^2-7x-2x+14=0$

$⇒(x-7)(x-2)=0$

$\therefore x = 7$ or $x = 2$

Here, the value of $x=7$.

Hence, the correct answer is $x^2-9x+14=0$.

Q10. One of the factors of the expression $4\sqrt{3}x^{2}+5x-2\sqrt{3}$ is:

1. $4x+\sqrt{3}$

2. $4x+3$

3. $4x-3$

4. $4x-\sqrt{3}$

Hint: Factorize the given expression using middle-term splitting to get the solution.

Answer:

$4\sqrt{3}x^{2}+5x-2\sqrt{3}$

= $4\sqrt{3}x^{2}+8x-3x-2\sqrt{3}$

= $4x(\sqrt{3}x+2)-\sqrt{3}(\sqrt{3}x+2)$

= $(4x-\sqrt{3})(\sqrt{3}x+2)$

Hence, the correct answer is $4x-\sqrt{3}$.

Q11. The term that should be added to ($4x^2+8x$) so that the resulting expression is a perfect square, is:

1. 2

2. 4

3. 2x

4. 1

Hint: Use Identity: $(a + b)^2 = a^2 + b^2 + 2ab$

Answer:

$4x^2+8x$ = $(2x)^2+2×(2x)×2$

Adding $4$ on both sides then use identity: $(a + b)^2 = a^2 + b^2 + 2ab$

$4x^2+8x+4$ = $(2x)^2+2×(2x)×2+4$ = $(2x+2)^2$

Thus, $4$ is to be added to $4x^2+8x$ to make it a perfect square.

Hence, the correct answer is $4$.