Unit digit

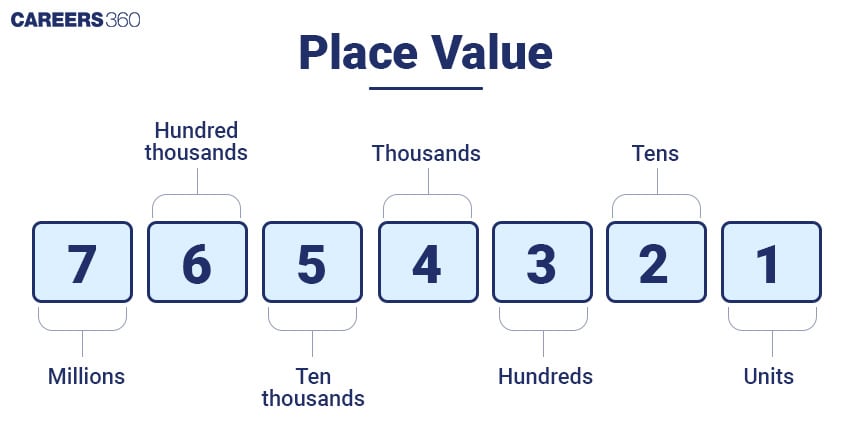
The place value system in Maths describes the position or place of a digit in a number. Each digit has a place in a number. The order of place value of digits of a number from right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on. For example, the place value of 5 in 7546 is 5 hundred or 500. However, the place value of 5 in 5432 is 5 thousand or 5000. Here, we can see that even though the digits are the same in both numbers, their place value changes with the change in their position. The unit digit, also known as the ones place, is the rightmost digit in a number. It provides essential information about the number's properties, such as its parity (whether it is even or odd) and its divisibility by small integers like 2, 5, and 10.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

This Story also Contains

1. Concept of unit digit in number system:
2. Concept of Cyclicity
3. How to find the unit digit of a number
4. Tips and Tricks to find the unit digit of a number:
5. Practice Questions

Similarly, the last two digits of a number are basically the tens place and units place digit of that number. So given a number say 2564, the last two digits of this number are 6 and 4. They are useful for understanding more complex divisibility rules, cyclic patterns, and sequences.

In this topic we will discuss various topics such as ‘unit digit’, ‘find the unit digit’, ‘tens and units digits’ etc.

Concept of unit digit in number system:

The concept of the unit digit is one of the most important topics in the competitive examinations. Students may find plenty of questions related to unit digits in the examination. By finding the unit digit we can decide whether a number is even or odd.

Concept of Cyclicity

It is easy to identify the Unit Place Digit of the smaller number but when it comes to the numbers raised to the larger power it becomes difficult to identify the same by simple observation. It is when the concept of cyclicity comes into the picture.

The cyclicity concept is based on the fact that every digit in the number has its own repetitive pattern when raised to any specific power.

For example,

2¹=2 (unit digit 2)

2²=4 (unit digit 4)

2³=8 (unit digit 8)

2⁴=16 (unit digit 6)

2⁵=32 (unit digit 2)

2⁶=64 (unit digit 4)

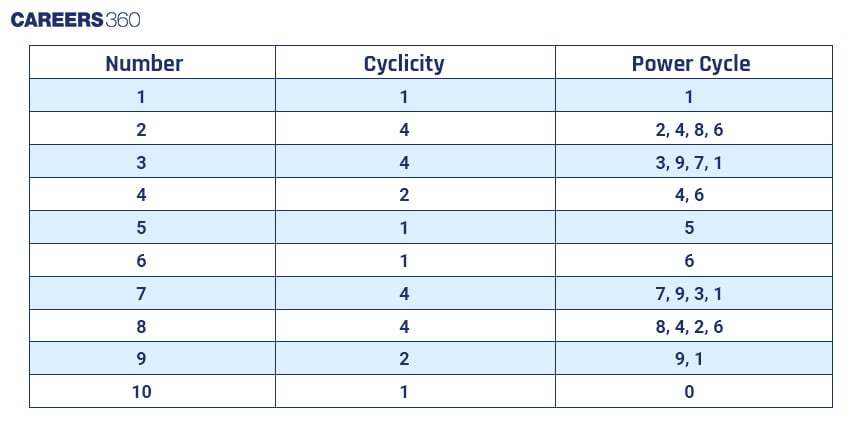
Here, the unit digits follow the sequence 2, 4, 8, 6, and then repeat. This implies that the cyclicity of digit 2 is 4. Similarly, the cyclicity of all other single-digit numbers can be evaluated.

Here is the cyclicity table for all numbers:

How to find the unit digit of a number

There are two types of problems when finding the unit digit of a number. We need to discuss them separately.

To find the unit digit of a number formed by multiplying the several numbers:

To find the unit digit of a number formed by multiplying several numbers, we need to only multiply the unit digits of those numbers.

For example: Find the unit digit of the number formed by 81 × 82 × 83 × 84 × 85 × 86 × 87 × 88 × 89.

Sol: Multiplying only the unit digits we get,

1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 ⇒ 2 × 2 × 0 × 6 × 9 ⇒ 0

So, the unit digit of the number is 0.

To find the unit digit of a number in the form of x n

To find the unit digit of a number in the form of x n we can classify the numbers into three parts:

x ending with 0, 1, 5, 6:

If we have the numbers ending with 0, 1, 5, and 6, then we get the same unit digit when raised to any power. So, the required unit digits are 0^?⇒0 ,1^?⇒1, 5^?⇒5 and 6^?⇒6 .

• The unit digit of the number ending with 0 is always 0.

• The unit digit of the number ending with 1 is always 1.

• The unit digit of the number ending with 5 is always 5.

• The unit digit of the number ending with 6 is always 6.

Example: Find the unit digit of 30²⁴, 41³⁶, 75⁴⁴, and 86³⁸.

Sol: The unit digit of 30²⁴ is 0.

The unit digit of 41³⁶ is 1.

The unit digit of 75⁴⁴ is 5.

The unit digit of 86³⁸ is 6.

x ending with 2, 3, 7, 8:

For the number ending with 2, we need to follow some steps to find the unit digit of the number.

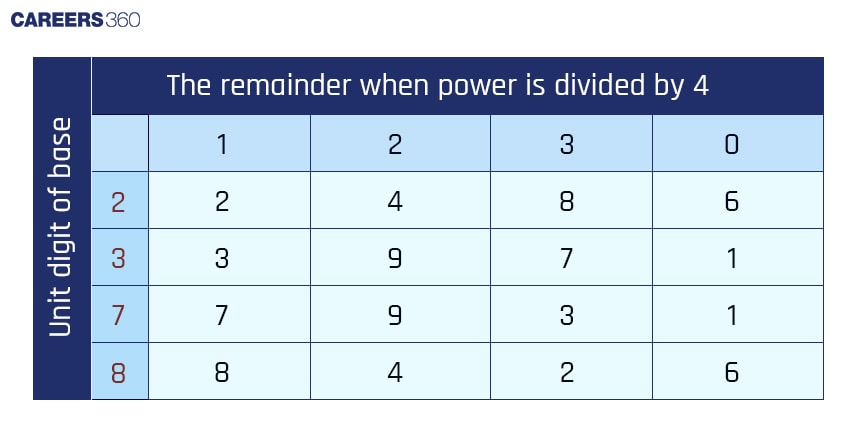
• Step 1: Divide the power of the given number i.e. ? by 4.

• Step 2: After the division, we get a remainder of 0 or 1 or 2 or 3.

• Step 3:

If the remainder is 1, then the unit digit is 2¹⇒2.

If the remainder is 2, then the unit digit is 2²⇒4.

If the remainder is 3, then the unit digit is 2³⇒8.

If the remainder is 0, then the unit digit is 2⁴⇒6.

Example: Find the unit digit of 4562⁷⁵.

Sol: The unit digit of 4562 is 2.

So, we divide 75 by 4 and get the remainder of 3.

Therefore, the required unit digit is 2³=8.

For the number ending with 3, we need to follow the below steps to find the unit digit of the number.

• Step 1: Divide the power of the given number i.e. ? by 4 .

• Step 2: After the division, we get a remainder of 0 or 1 or 2 or 3.

• Step 3:

If the remainder is 1, then the unit digit is 3¹⇒3.

If the remainder is 2, then the unit digit is 3²⇒9.

If the remainder is 3, then the unit digit is 3³⇒7.

If the remainder is 0, then the unit digit is 3⁴⇒1.

Example: Find the unit digit of 563²⁶.

Sol: The unit digit of 563 is 3.

So, we divide 26 by 4 and get the remainder of 2.

Therefore, the required unit digit is 3²=9.

For the number ending with 7, we need to follow the given steps to find the unit digit of the number.

• Step 1: Divide the power of the given number i.e. ? by 4.

• Step 2: After the division, we get a remainder of 0 or 1 or 2 or 3.

• Step 3:

If the remainder is 1, then the unit digit is 7¹⇒7.

If the remainder is 2, then the unit digit is 7²⇒9.

If the remainder is 3, then the unit digit is 7³⇒3.

If the remainder is 0, then the unit digit is 7⁴⇒1.

Example: Find the unit digit of 2587¹¹³.

Sol: The unit digit of 2587 is 7.

So, we divide 113 by 4 and get the remainder of 1.

Therefore, the required unit digit is 7¹=7.

For the number ending with 8, we need to follow the below steps to find the unit digit of the number.

• Step 1: Divide the power of the given number i.e. ? by 4.

• Step 2: After the division, we get a remainder of 0 or 1 or 2 or 3.

• Step 3:

If the remainder is 1, then the unit digit is 8¹=8.

If the remainder is 2, then the unit digit is 8²⇒4.

If the remainder is 3, then the unit digit is 8³⇒2.

If the remainder is 0, then the unit digit is 8⁴⇒6.

Example: Find the unit digit of 6368⁸⁴.

Sol: The unit digit of 6368 is 8.

So, we divide 84 by 4 and get the remainder of 0.

Therefore, the required unit digit is 8⁴⇒6.

x ending with 4, 9:

Both the numbers 4 and 9 have a cyclicity of 2.

So, there are two cases for each number:

x ending with 4:

• If the Power of 4 is Even, the unit digit will be 6.

• If the Power of 4 is Odd, the unit digit will be 4.

x ending with 9:

• If the Power of 9 is Even, the unit digit will be 1.

• If the Power of 9 is Odd, the unit digit will be 9.

Example: Find the unit digit of 564⁴⁸.

Sol: The unit digit of 564 is 4 and the power 48 is an even number.

So, the unit digit of 564⁴⁸ is 6.

Let’s take another example:

Find the unit digit of 8759⁸³.

Sol: The unit digit of 8759 is 9 and the power 83 is an odd number.

So, the unit digit of 564⁴⁸ is 9.

Tips and Tricks to find the unit digit of a number:

• The unit digit of any number ending with 0, 1, 5, or 6 raised to any power will have the same unit digit as the number itself.

• The unit digit of any number ending with 4 or 9, check the power if it's odd or even, then calculate as shown above.

• The unit digit of any number ending with 2, 3, 7, or 8, check their cyclicity and calculate as shown above.

• Squares of numbers ending with 2 or 8 have the unit digit of 4.

• Squares of numbers ending with 3 or 7 have the unit digit of 9.

• Squares of numbers ending with 4 or 6 have the unit digit of 6.

Practice Questions

Q.1. What is the unit digit of ( 217 ) 413 × ( 819 ) 547 × ( 414 ) 624 × ( 342 ) 812 ?

1. 2

2. 4

3. 6

4. 8

Hint: Use the concept of cyclicity to get the desired unit digit.

Solution:

Given:

(217)413 × (819)547 × (414)624 × (342)812

Solution:

The cyclicity of 7 is 4.

The cyclicity of 9 is 2.

The cyclicity of 4 is 2.

The cyclicity of 2 is 4.

According to the cyclicity theorem, divide the powers by 4 and take reminders. Otherwise, take 4.

The unit digit of (217)413 = 7413 = 7(4 × 103) + 1 = 71 = 7

The unit digit of (819)547 = 9547 = 9(2 × 273) + 1 = 91 = 9

The unit digit of (414)624 = 4624 = 4(2 × 312) = 44 = 6

The unit digit of (342)812 = 2812 = 2(4 × 203) = 24 = 6

The unit digit of the given expression will be the same as the unit digit of 7413 × 9547 × 4624 × 2812

⇒ 71 × 93 × 44 × 24

For unit digit ⇒ 7 × 9 × 6 × 6

∴ The required unit digit = 8

Hence, the correct answer is option (4).

Q.2. What is the digit in the unit's place in the number 15 ! 100 ?

1. 5

2. 7

3. 3

4. 0

Hint: Number of trailing zeroes in n ! = [ n 5 ] + [ n 25 ] + [ n 125 ] + ....... where [ ] denotes greatest integer function.

Solution:

Number of trailing zeroes in n ! = [ n 5 ] + [ n 25 ] + [ n 125 ] + ....... where [ ] denotes greatest integer function.

So, the number of trailing zeroes in 15! = [ 15 5 ] + [ 15 25 ] + [ 15 125 ] + ....... = 3 + 0 + 0 + ..... = 3

⇒ Number of zeroes in the product = 3

⇒ Unit's digit in 15 ! 100 = 0

Hence, the correct answer is option (4).

Q.3. What will be the remainder when 252 126 + 244 152 is divided by 10?

1. 4

2. 6

3. 0

4. 8

Hint: When any number is divided by 10, the unit digit will be the remainder.

Solution:

To find the remainder when 252 126 + 244 152 is divided by 10, we only need to consider the unit digit of each term in the sum.

The unit digit of 252 126 is the same as the unit digit of 2126.

Divide 126 by 4 and get remainder = 2

So, the unit digit of 252 126 is 2 2 = 4

The unit digit of 244 152 is the same as the unit digit of 4152.

If the power of 4 is even, the unit digit is 6.

So, the unit digit of 244 152 is 6.

The sum of the unit digits = 4 + 6 = 10

The remainder when 252 126 + 244 152 is divided by 10 = Remainder when 10 is divided by 10 = 0

So, the remainder is 0.

Hence, the correct answer is option (3).

Q.4. Let x = (433)24 – (377)38 + (166)54. What is the unit digit of x ?

1. 8

2. 9

3. 7

4. 6

Hint: The unit digit of the power of a number repeats itself every 4th time for the base having the last digit as 3 or 7. But the last digit for the(166)54 will always be 6 as the unit digit of a power of a number having the last digit 6 will always be 6.

Solution:

Given: x = (433)24 – (377)38 + (166)54

We can write 43324 = 433(4 × 5) + 4, 37738 = 377(4 × 9) + 2

So, the unit digit of 4334 = 1 and the unit digit of 3772 = 9

The last digit for the(166)54 will always be 6 as the unit digit of a power of a number having the last digit 6 will always be 6.

∴ x = 1 – 9 + 6 = 7 – 9 → Unit digit = 17 – 9 = 8

Hence, the correct answer is option (1).

Q.5. Find the Unit digit of 287 5 62581 .

1. 1

2. 2

3. 7

4. 4

Hint: Use the cyclicity of 7.

Solution:

The unit digit of 2587 is 7.

So, we divide the power 562581 by 4 and get the remainder of 1.

Therefore, the required unit digit is 7 1 = 7 .

Hence, the correct answer is option (3).

Q.6. The unit digit in the sum of ( 124 ) 3 72 + ( 124 ) 3 73 is:

1. 5

2. 4

3. 20

4. 0

Hint: If the power of a number ending with 4 is even, then the unit digit will be 6 and if it is odd then, the unit digit will be 4.

Solution:

Both of the numbers have a unit digit of 4 and it has a repeating cycle of 2 with unit digits 4 and 6

So in the first number power is 372 which is an even number, the unit digit of the first number will be 6.

Also in the second number power is 373 which is an odd number, the unit digit of the second number will be 4.

Therefore, the unit digit of the sum will be 6 + 4 → 0.

Hence, the correct answer is option (4).

Q.7. The digit in the unit digit in the square of 66049 is:

1. 1

2. 2

3. 3

4. 4

Hint: The square of numbers ending with 9 has the unit digit of 1.

Solution:

We know, the square of numbers ending with 9 has the unit digit of 1.

So, the unit digit in the square of 66049 is 1.

Hence, the correct answer is option (1).

Q.8. Find the unit digit in 71 × 72 × 73 × 74 × 76 × 77 × 78 × 79.

1. 1

2. 4

3. 6

4. 3

Hint: We need to multiply only the unit digits.

Solution:

The unit digit of 71 × 72 × 73 × 74 × 76 × 77 × 78 × 79

→ 2 × 2 × 2 × 2 → 6.

Hence, the correct answer is option (3).

Q.9. Find the unit digit of the sum of the first 110 natural numbers.

1. 2

2. 3

3. 5

4. 4

Hint: The sum of the first n natural numbers = n ( n + 1 ) 2 .

Solution:

The sum of the first 110 natural numbers

= 110 × ( 110 + 1 ) 2 = 110 × 111 2 = 55 × 111

So, the unit digit of the sum of the first 110 natural numbers = 5 × 1 = 5.

Hence, the correct answer is option (3).

Q.10. Find the unit digit of 432 4 12 × 499 4 31 .

1. 4

2. 3

3. 2

4. 1

Hint: Use the cyclicity of numbers to solve this.

Solution:

For the first number,

We divide 412 by 4 to get the remainder of 0.

So, the unit digit of 432 4 12 is 2 4 → 6.

Also, for the second number,

The unit digit of the number 499 is 9 and the power 431 is odd.

So, the unit digit of 499 4 31 is 9.

Therefore, the unit digit of 432 4 12 × 499 4 31 is 6 × 9 → 4.

Hence, the correct answer is option (1).