What is a Factor?
In mathematics, a factor of a number is a divisor of the given number that divides it completely without leaving any remainder. Prime numbers only have two factors i.e. 1 and the number itself, whereas composite numbers have multiple factors. For example, 1, 2, 3, 4, 6, and 12 are the factors of the number 12 and for the prime number 5, the factors are 1 and 5.
CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts
XAT 2025: Section-wise Preparation Tips | Sample Paper
Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers
- Prime factorization of a number
- How to find a factor?
- Factors of a polynomial
- Some important results/properties of the factor
- Defining Perfect Number:
- Some important results/properties of multiple
- Practice questions

Also, factors of a number can be positive or negative integers but they can’t be fractions or decimals. While learning the number system, ‘how to find the factors’ is important. In this article, we will learn how to calculate prime factors, how to find all factors of a number, how to factor numbers etc.
Prime factorization of a number
Prime factorization is a method where a number is expressed as a product of its prime factors. A prime number is a number that has exactly two factors i.e. 1 and the number itself. For example, if we take the number 12. We know that 12 = 3 × 4, but 4 is not a prime number. The number 4 can further be factorized as 2 × 2, where 2 is a prime number. Therefore, the prime factorization of 12 = 3 × 2 × 2, where all the factors are prime numbers.
Now let's find the prime factorization of 120.
120 = 2 × 2 × 2 × 3 × 5 = $2^3 × 3 × 5$
So, the prime factorization of 120 is $2^3 × 3 × 5$.
Let's look at a few other examples of prime factorization:
30 = 2 × 3 × 5
48 = $2^4 × 3$
80 = $2^4 × 5$
150 = $2 × 3 × 5^2$
180 = $2^2 × 3^2 × 5$
How to find a factor?
Finding factors of a given number involves identifying those integers that can completely divide the original number without leaving any remainder.
Finding factors using the division method
To find all the factors of a number using the division method, divide the number by all the natural numbers less than the given number. Identify the numbers that completely divide the given number. Let us take an example to understand this more easily.
Find the factors of 12.
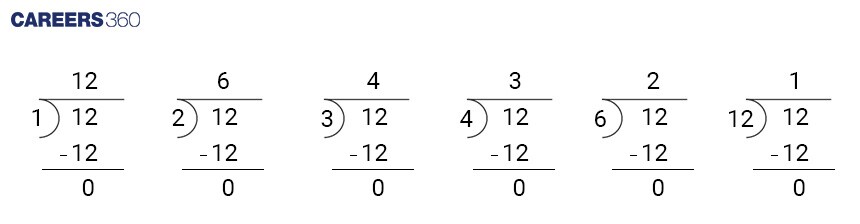
Division and the remainder | Is the number a factor of 12? |
12 $\div$ 1 = 12 and the remainder is 0 | Yes, 1 is a factor of 12. |
12 $\div$ 2 = 6 and the remainder is 0 | Yes, 2 is a factor of 12. |
12 $\div$ 3 = 4 and the remainder is 0 | Yes, 3 is a factor of 12. |
12 $\div$ 4 = 3 and the remainder is 0 | Yes, 4 is a factor of 12. |
12 $\div$ 5 = 2 and the remainder is 2 | No, 5 is not a factor of 12. |
12 $\div$ 6 = 2 and the remainder is 0 | Yes, 6 is a factor of 12. |
12 $\div$ 7 = 1 and the remainder is 5 | No, 7 is not a factor of 12. |
12 $\div$ 8 = 1 and the remainder is 4 | No, 8 is not a factor of 12. |
12 $\div$ 9 = 1 and the remainder is 3 | No, 9 is not a factor of 12. |
12 $\div$ 10 = 1 and the remainder is 2 | No, 10 is not a factor of 12. |
12 $\div$ 11 = 1 and the remainder is 1 | No, 11 is not a factor of 12. |
12 $\div$ 12 = 1 and the remainder is 0 | Yes, 12 is a factor of 12. |
Therefore, the factors of 12 are 1, 2, 3, 4, 6, and 12.
Again we take a look at another method to find the factors of a number.
Finding factors using the multiplication method
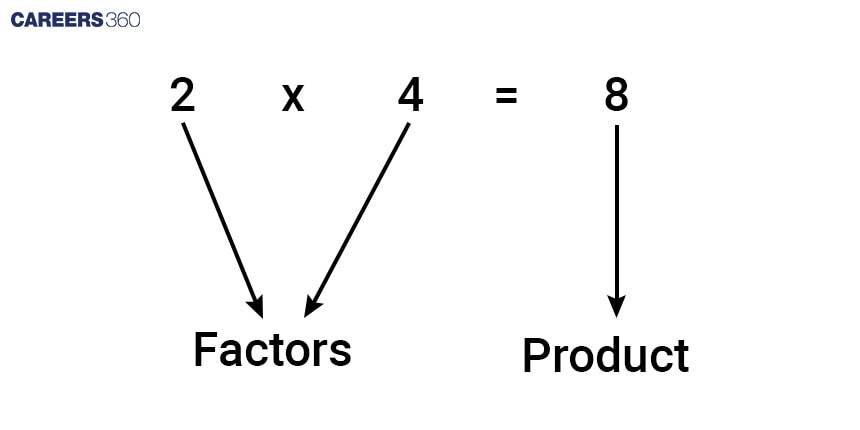 If we can express the given number as the product of two integers, then the numbers being multiplied are factors of the product.
If we can express the given number as the product of two integers, then the numbers being multiplied are factors of the product.
So, to find all the factors of a number, find all the pairs of numbers that, when multiplied, give the given number as a product. Let us take an example to understand this clearly.
Find the factors of 18.
18 can be written as,
18 = 1 × 18
18 = 2 × 9
18 = 3 × 6
Therefore, the factors of 18 are 1, 2, 3, 6, 9, and 18.
To find the factors of large numbers use the prime factorization method.
divide the numbers with the least prime number, i.e. 2. If the number is not divisible by 2, move to the next prime number, i.e. 3, and so on until 1 is reached. Let us take an example.
Find the prime factors of 540.
Steps | Prime factors | Division |
Divide 540 by 2 | 2 | 540 $\div$ 2 = 270 |
Divide 270 by 2 | 2 | 270 $\div$ 2 = 135 |
Divide 135 by 3 | 3 | 135 $\div$ 3 = 45 |
Divide 45 by 3 | 3 | 45 $\div$ 3 = 15 |
Divide 15 by 3 | 3 | 15 $\div$ 3 = 5 |
Divide 5 by 5 | 5 | 5 $\div$ 5 = 1 |
Therefore, the prime factors of 540 are 2, 2, 3, 3, 3, and 5.
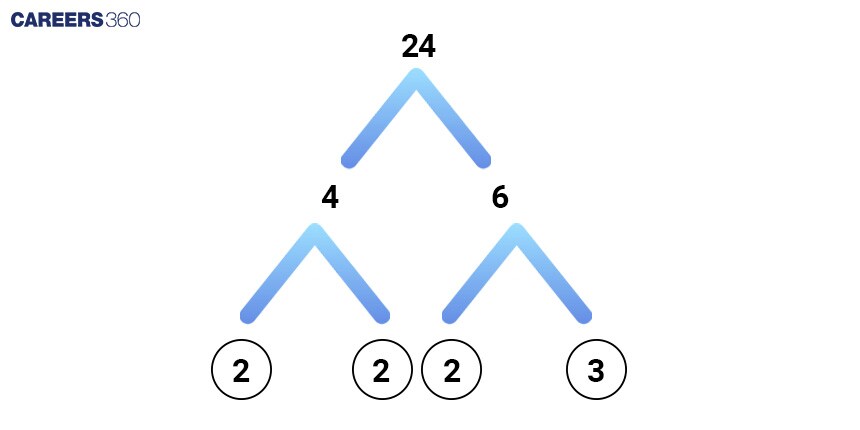
Factor Tree
One of the easiest ways for children to calculate factors is to use a factor tree. This is a simple method used to work out which numbers can be multiplied together to reach a product. As well as being an effective strategy, it is also highly visual.
Let’s find the factors of 24 using the factor tree:
Factors of a polynomial
Finding the factors of a polynomial involves expressing the polynomial as a product of its simpler polynomial factors. There are multiple methods to find the factors of a polynomial.
Method of common factors:
This is the simplest method of factoring a polynomial by taking common factors of each of the terms. At first, the factors of each of the terms of the polynomial are written. Further, the common factors across the terms are taken to obtain the possible factors. This is equivalent to using the distributive property in reverse. Let us understand this better with the help of an example.
Factorize $9y^3 + 6y^2$
= $3 × 3 × y × y × y + 2 × 3 × y × y$
= $3y^2 × (3y + 2)$
So, the factors of $9y^3 + 6y^2$ are $3y^2$ and $(3y + 2)$.
Finding factors using the grouping method:
Here, the given polynomial is distributed in pairs or grouped in pairs to find the factors. Let us try to understand grouping for factorizing with the help of the following example.
Factorize $x^3 + 2x^2 + 3x + 6$.
Here, $x^3 + 2x^2 + 3x + 6$
= $x^2(x+2)+3(x+2)$
= $(x+2)(x^2+3)$
So, the factors of $x^3 + 2x^2 + 3x + 6$ are $(x+2)$ and $(x^2+3)$.
Using the algebraic identities:
Factorization can also be done using some algebraic identities. The most common identities used in factorization are:
$a^2 - b^2 = (a+b)(a-b)$
$a^3 + b^3 = (a+b)(a^2-ab+b^2)$
$a^3 - b^3 = (a-b)(a^2+ab+b^2)$
Let’s see an example
Factorize $x^2 - 100$
= $x^2 - 10^2$
= $(x+10)(x-10)$
Let’s take another example
Factorize $x^3+8$
= $x^3+2^3$
= $(x+2)(x^2-2x+4)$
Factor theorem:
For a polynomial p(x) of degree greater than or equal to one,
(x - a) is a factor of p(x), if p(a) = 0
If p(a) = 0, then (x - a) is a factor of p(x)
Where ‘a’ is a real number.
For example, let p(x) = $x^2+x-2$
Now, p(1) = $1^2+1-2$ = 0
So, (x - 1) is a factor of $x^2+x-2$.
Some important results/properties of the factor
The number of factors of a given number is finite. For example, factors of 6 are 1, 2, 3, and 6.
Every factor is less than or equal to the given number, it can never be bigger than the number. For example, each factor of 12 i.e. 1, 2, 3, 4, 6, and 12 is less than or equal to 12.
Except for 0 and 1, every integer has a minimum of two factors, 1 and the number itself.
The smallest factor of any number is 1.
The largest factor of any number is the number itself.
Factors can be evaluated using both multiplication and division methods.
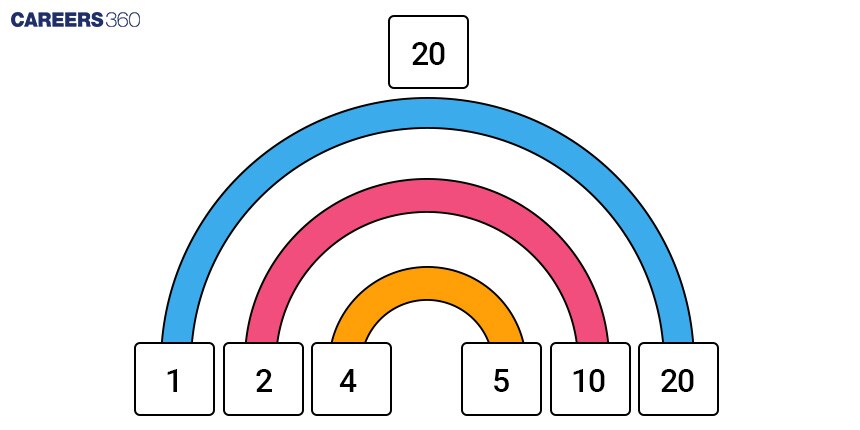
Factors come in pairs: If a is a factor of number n, then $\frac{n}{a}$ is also a factor of n. For example, 4 is a factor of 20 thus $\frac{20}{4}$ = 5 is also a factor of 20.
Defining Perfect Number:
A perfect number is a positive integer that is equal to the sum of its factors except for the number itself. In other words, a perfect number is defined as a positive integer that can be expressed as the sum of its proper factors (factors except for the number itself). The smallest perfect number is 6, which is the sum of its factors i.e. 1, 2, and 3. It is to be noted that this sum does not include the number itself which is also a factor of itself. Another example of a perfect number is 28 as it is also equal to the sum of its divisors.

Some important results/properties of multiple
A multiple of a number can be defined as a product of the given number and any other natural number. For example, multiples of 3 are 3, 6, 9, 12, 15, etc.
Here are some important results or properties of multiple:
Every multiple of a number is greater than or equal to that number. For example, every multiple of 5 i.e. 5, 10, 15, 20, …. is greater than or equal to 5.
Every non-zero number has an infinite number of multiples. For example, multiples of 2 are 2, 4, 6, 8, 10, …..
Every number is a multiple of itself. For example, 7 is a multiple of 7.
If m is the multiple of n, then m is completely divisible by n without leaving any remainder. For example, 10 is a multiple of 2, thus $\frac{10}{2}$ = 5, and the remainder is 0.
Any number multiplied by zero is zero. Thus, zero is a multiple of every number.
Practice questions
Q.1. All the factors of the number 15 are:
(1) 5, 10, 15, 1
(2) 1, 3, 5, 15
(3) 3, 5, 7, 9
(4) 1, 2, 3, 15
Solution:
2, 7, or 10 can’t be a factor of 15 as they don’t divide 15 completely.
So, all the factors of 15 are 1, 3, 5, 15.
Hence, the correct answer is option (2).
Q.2.Every number is the greatest factor of itself. (True/False)
True
False
Solution:
Factors have a property that states that the largest factor of any number is the number itself.
Hence, the correct answer is option (1).
Q.3. A number that is the factor of every number is:
0
2
1
3
Solution:
1 is the factor of every number.
Hence, the correct answer is option (3).
Q.4. What are the prime factors of 20?
2 and 5
3 and 5
4 and 5
5 and 10
Solution:
Factors of 20 are 1, 2, 4, 5, 10, and 20.
So, the prime factors of 20 are 2 and 5.
Hence, the correct answer is option (1).
Q.5. What are the common factors of 24 and 36?
1, 2, 3, 4, 5, 6, 12
1, 2, 4, 6, 12
1, 2, 3, 4, 6
1, 2, 3, 12, 24
Solution:
Factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
So, the common factors of 24 and 36 are 1, 2, 3, 4, 6, and 12.
Hence, the correct answer is option (2).
Q.6. Factorize $2x^2-162$.
$(2x+9)(x-9)$
$2x(x-81)$
$2(x+9)(x-9)$
$(2x+9)(2x-9)$
Solution:
Given: $2x^2-162$
= $2(x^2-81)$
= $2(x^2-9^2)$
= $2(x+9)(x-9)$
Hence, the correct answer is option (3).
Q.7. Factorize $x^2+2x-3$.
$(x+3)(x+1)$
$(x-3)(x-1)$
$(x-3)(x+1)$
$(x+3)(x-1)$
Solution:
Given: $x^2+2x-3$
= $x^2+2x+1-4$
= $(x+1)^2-2^2$
= $(x+1+2)(x+1-2)$
= $(x+3)(x-1)$
Hence, the correct answer is option (4).
Q.8. Factorize $8x^3+125$.
$(2x+5)(4x^2-10x+25)$
$(4x+5)(4x^2-10x+25)$
$(2x-5)(4x^2+10x+25)$
$(8x+5)(4x^2+20x+5)$
Solution:
Given: $8x^3+125$
= $(2x)^3+(5)^3$
= $(2x+5)[(2x)^2-(2x)(5)+(5)^2]$
= $(2x+5)(4x^2-10x+25)$
Hence, the correct answer is option (1).
Q.9. Factorize $27y^3-512$.
$(3y+8)(9y^2-24y+64)$
$(3y-8)(9y^2+24y+64)$
$(6y-8)(12y^2+24y+36)$
$(27y-512)(27y^2+248y+512)$
Solution:
Given: $27y^3-512$
= $(3y)^3-(8)^3$
= $(3y-8)[(3y)^2+(3y)(8)+(8)^2]$
= $(3y-8)(9y^2+24y+64)$
Hence, the correct answer is option (2).
Q.10. Find one factor of $x^3-2x^2+3x-6$.
(x+2)
(x-1)
(x-2)
(x+1)
Solution:
Let f(x) = $x^3-2x^2+3x-6$
Now, f(2) = $(2)^3-2(2)^2+3(2)-6$ = $8-8+6-6$ = 0
Therefore, (x-2) is a factor of f(x).
Hence, the correct answer is (3)