Arithmetical Problems: Meaning, Reasoning Questions, Examples

Arithmetical Problems are defined as solving logical reasoning questions by performing various mathematical operations. Some important chapters come under arithmetic reasoning such as Average, Percentage, Profit and Loss, Problem on ages, Time and Work, Mensuration etc. Arithmetic reasoning questions are generally seen in the SSC, Railways, Defence, and Insurance exams.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: IBSAT 2024 Mock Tests | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

Question with Solutions: Missing Number | Alphabet Test | Arithmatical Problems | Calendar

This Story also Contains

1. Overview of Common Types of Arithmetic Problems Encountered in Reasoning Tests
2. 1. Average Problems in Reasoning
3. 2. Problems on Ages in Reasoning
4. 3. Time and Work Problems in Reasoning
5. 4. Simplification in Reasoning
6. 5. Time and Distance Problems in Reasoning
7. 6. Percentage Problems in Reasoning
8. 7. Ratio and Proportion Problems in Reasoning
9. 8. Mensuration Problems in Reasoning
10. 9. Profit and Loss Problems in Reasoning
11. Arithmetic Questions with Answers
12. Arithmetical Problems for SSC MTS/ SSC CHSL/ SSC Stenographer/ RRB exams
13. Arithmetical Problems for IBPS RRB Assistant/ IBPS CWE Clerical/ Insurance Assistant exams

Overview of Common Types of Arithmetic Problems Encountered in Reasoning Tests

The common types of arithmetic problems include simplification such as addition, subtraction, multiplication and division as well as age, average, percentage problems, decimal and fraction problems, mensuration etc. In reasoning tests basic questions from these chapters have been asked from the aspirants.

1. Average Problems in Reasoning

Average problems in reasoning are seen in many competitive exams and entrance exams. In reasoning, there are simple average problems seen such as the average of prime numbers, natural numbers, the average of multiples of different numbers, and the average marks of the students etc.

Definition of Average

The average is defined as the mean value which is equal to the ratio of the sum of the observations of a given set of values to the total number of observations in the given set.

Methods to Calculate the Average

The important formulas to calculate average:
1) Average = Sum of Observations/ Number of Observations
2) Average speed = (2ab)/ a + b (Let’s a man cover a certain distance at a kmph and an equal distance at b kmph then to calculate the average speed of the whole journey use the above formulae)
Arithmetic problems examples:
Example: Find the average of the first 50 natural numbers.
Solution:
The sum of the first n natural numbers = n(n +1)/ 2
So, the sum of the first 50 natural numbers = 50 x 51/ 2 = 1275
Required average = Sum of Observations/ Number of Observations
= 1275/ 50 = 25.5
Example: There are two sections C and D of a class, consisting of 40 and 44 students respectively. If the average weight of section C is 44 kg and that of section D is 55 kg. Find the average weight of the whole class.
Solution:
Total Weight of (40 + 44) students = ( 40 x 44 + 44 x 55) kg = 4180 kg
Therefore, the average weight of the whole class = (4180/ 84) kg = 49.76 kg.

2. Problems on Ages in Reasoning

The questions are asked in various exams such as in entrance exams and competitive exams. These questions are solved using the algebraic equations. In these questions, an aspirant has to determine the age of an individual or a group of persons according to the question. These questions are a bit confusing but by practice an aspirant gains a good understanding of these questions.

Concept of Basic arithmetic problems of Ages

1) If the age given is in the form of a ratio, for example, a : b then the age will be considered as ax and bx.
2) If the current age is X, then the age n years later = x + n.
3) If the current age is X, then the age n years ago = x - n.

Techniques to tackle arithmetic problem solving age-related reasoning questions.

1) First of all, read the information given in the question carefully. Then assume the unknown age to be some number or variable. Let’s assume ‘X’ or ‘Y’.
2) Convert the information given in the question into mathematical equations to solve the question accurately.
3) Now calculate the variable by solving the mathematical equations and check that the obtained value must satisfy the conditions given in the question.
4) Practice is a key to success an aspirants should start their practice from simple arithmetic questions and answers pdf available online.

Example:
Directions: The sum of the present ages of Vishal and Aditi is 105 years. If Aditi is 25 years younger than Vishal, then what will be the present age of Pritam, who is 7 years older than Adit?

1) 40 years

2) 72 years

3) 32 years

4) 47 years

Solution:

Given:

(I) The sum of the present ages of Vishal and Aditi is 105 years.

(II) If Aditi is 25 years younger than Vishal
According to the statements –

(I) V's age + A's age = 105

(II) A's age = V's age – 25

⇒V's age = A's age + 25 (Put the value of V's age in equation I)

⇒A's age + 25 + A's age = 105

2 × A's age + 25 = 105

2 × A's age = 80

A's age = 40

Pritam's age = 7 + A's age; Pritam's age = 7 + 40 = 47

So, the present age of Pritam is 47 years. Hence, the fourth option is correct.

3. Time and Work Problems in Reasoning

Time and work deal with the time taken by a person or group to complete a piece of work. It is also used to calculate the efficiency of a person or group to complete a task. Generally, one question is seen in various exams from this chapter.

Time and Work Concept

1) Work Done (W) = Time (T) x Rate of Work (R)
It takes time (T) to complete a certain amount of work (W). Thus, the number of units of work done per unit of time is called the rate of work (R)
2) Rate of work and Time are inversely proportional to each other. Thus, R = 1/T

Formulas and Methods of Arithmetic problem solving Time and Work Problems in Reasoning

1) If X can do a piece of work in n days, then X’s one-day work is equal to 1/n.
2) If X’s 1 day’s work is equal to 1/n, then X can finish the work in n days.
3) If X is twice as good a workman as Y, then:
The ratio of work done by X and Y = 2 : 1
The ratio of time taken by X and Y to finish a work = 1 : 2
4) A : B is the ratio of the number of men who are required to complete a given task, then the ratio of the time taken by them to complete the work will be B : A.
5) If x number of people can do W1 work in D1 days, working T1 hours each day and the number of people can do W2 work in D2 days, working T2 hours each day, then the relation between them will be M1 x D1 x T1 / W1 = M2 x D2 x T2 / W2

Arithmetic problems examples:

Example: Raju and Ramu together can do a piece of work in 8 days, and Raju alone can do it in 12 days. In how many days can Ramu alone do it?

1) 18 days

2) 20 days

3) 22 days

4) 24 days

Solution:
If a man can do the work in n days, then 1 day's work of the man is 1/n.
Raju and Ramu together can do a piece of work in 8 days.

Their 1 day's work = 1/8

Raju alone can do it in 12 days.

Raju's 1 day's work = 1/12

So, Ramu's 1 day's work = 1/ 8 - 1/ 12 = 1/24
Therefore, Ramu can complete the work alone in 24 days. Hence, the correct answer is 24 days.

Example: A, B, and C are employed to do a piece of work for INR 5,290. A and B together are supposed to do 19/23 of the work and B and C together 8/23 of the work. Then A should be paid:

1) INR 4,250
2) INR 3,450
3) INR 1,950
4) INR 2,290

Solution:

Part of the work done by A and B together = 19/23 of the total work

Part of the work done by B and C together = 8/23 of the total work

Part of the work done by A alone

= Total work – Part of work done by B and C together

= (1 – 8/23) of total work

= 15/23 of total work

Total wages = INR 5,290

So, the wage of A = 15/23 × 5290 = INR 3,450

Hence, the correct answer is INR 3,450

4. Simplification in Reasoning

Simplification is defined as simplifying or evaluating the numerical expression, equation or any word problem. In reasoning, it consists of basic questions which are solved by using the BODMAS method or by making a simple equation. Generally, 1- 2 questions are seen in the competitive and entrance exams from this chapter in the reasoning section.

Methods to Simplify Numerical Expressions

To solve the numerical expressions you have to apply the BODMAS rule. This rule depicts the correct order in which the mathematical operations are to be performed. So, as to find out the value of the given numerical expression.
Here, ‘B’ stands for ‘Bracket’, ‘O’ stands for ‘of’, ‘D’ for ‘Division’, ‘M’ for ‘Multiplication’, ‘A’ for ‘Addition’ and ‘S’ for ‘ Subtraction.
Therefore, in simplifying the expression, first of all, brackets must be removed in the order (), {}, [].
After removing brackets, we should use the following expressions strictly in the order:
Of, Division, Multiplication, Addition, and Subtraction

Arithmetic problem solving examples :

Example:
Directions: On a farm, there are 48 ducks, 42 goats, and 10 cows with some attendants. If the total number of feet is 216 more than the number of heads, what is the number of attendants on the farm?

1) 10

2) 14

3) 8

4) 12

Solution:
Given:

Number of Ducks = 48, Goats = 42 goats, Cows = 10 cows

Let the number of attendants be a.

Total number of feet of 48 ducks = 48 × 2 = 96

Total number of feet of 42 goats = 42 × 4 = 168

Total number of feet of 10 cows = 10 × 4 = 40

Total number of feet of a attendants = 2 × a = 2a

Each one has one head.

Total Heads = 48 + 42 + 10 + a = 100 + a
Total feet = 96 + 168 + 40 + 2a = 304 + 2a

Now according to the given question,

Total number of feet = Total number of heads + 216

(304 + 2a) = (100 + a) + 216

304 + 2a = 100 + a + 216

304 + 2a = 316 + a

2a – a = 316 – 304

a = 12

So, the total number of attendants on the farm is 12. Hence, the fourth option is correct.

Example:
Question: What is the value of (1665 ÷ 37) + (42 × 5)?

1) 295

2) 270

3) 255

4) 285

Solution:

Given, (1665 ÷ 37) + (42 × 5)

= 45 + 210

= 255

Hence, the correct answer is 255.

5. Time and Distance Problems in Reasoning

Speed, Time and Distance is one of the most important chapters. It tells us the distance covered by an object in a certain time at a certain speed or vice versa. In reasoning mostly one question is seen in the competitive exams. The basic question from this chapter is asked in the logical reasoning section which is solved by putting the values in the formulae. The formulas are discussed below.

Understanding the Relationship Between Time, Speed, and Distance

1) Speed = Distance/ Time
The relation between the above terms tells us how slow or fast an object moves. It defines the distance travelled by the time taken to cover the distance.

2) Speed is directly proportional to the distance travelled and inversely proportional to the time.
Therefore, Distance = Speed x Time
Time = Distance/ Speed

3) The speed, distance and time can be expressed in different units such as:
Distance: meters (m), kilometers(km), miles, feet
Time: seconds (s), minutes (min), hours (hr)
Speed: m/s, km/hr
Note: If the units of distance and time are equal to km and hr, then Speed will be km/hr as Speed = Distance/ Time

Formulas to Solve Time and Distance Problems in Reasoning

1) Speed = Distance/ Time
2) Time = Distance/ Speed
3) Distance = Speed x Time
4) a km/ hr = a x 5/18 m/ sec
5) b m/ sec =b x 18/ 5 km/hr
6) If the ratio of the speeds of X : Y , then the ratio of the time taken by them to cover the same distance is equal to 1/X : 1/Y or Y : X
7) Suppose a person covers a certain distance at a km/hr and an equal distance at b km/ hr. Then the average speed during the whole journey is (2ab/ a + b) km/hr

Example:
Directions: A person covers a certain distance in 6 hours if he travels at 40 km/hr. If he has covered the same distance in 4 hours, then his speed must be:

1) 50 km/hr

2) 60 km/hr

3) 80 km/hr

4) 70 km/hr

Solution:

The person covers a certain distance in 6 hours if he travels at 40 km/hr.

Speed = Distance/ Time

Distance covered in 6 hours = 6 × 40 = 240 km

To cover the same distance in 4 hours, then his speed must be

240/ 4 = 60 km/hr

Hence, the correct answer is 60 km/hr.

6. Percentage Problems in Reasoning

Percentage is defined as the number, amount, rate, etc of something expressed as if it is part of a total which is a hundred or a part or share of a whole or a percentage is a number or ratio that can be expressed as a fraction of 100. In reasoning, easy percentage problem is asked in various competitive and entrance exams. Mostly, one question is asked in the reasoning section of this concept.

Percentage Concepts

The word Percentage is derived from the Latin word “per centum” which means by the hundred.
The sign of percentage is %. For example: If we say 7%, then it is equal to 7/100 = 0.07

By a certain percentage, we mean that many hundredths. Therefore, a per cent means a hundredths, which is denoted by a%

1) To express a % as a fraction: a % = a /100
Therefore, 30% = 30/ 100 = 0.3, 56% = 56/100 = 0.56

2) To express a/b as a percent: a/b = (a/b x 100)%
Therefore, ¼ = (¼ x 100)% = 25%

Methods to Solve Percentage-Related Problems in Reasoning

1) First of all, write the percentage as a decimal or a fraction. Then divide the fraction or decimal by the part. This method is implemented in any situation in which the percentage and its value are given.

2) The three components of a per cent problem are Base, Rate, and Part.
Here Base = whole, total number of parts, Rate = a per cent, Part = part of the base
Rate = Part/ Base
Percentage(%) = Number of Parts/ Total number of parts

Arithmetic problems examples:

Example:
Directions: A student has to obtain 40% of the maximum marks to pass. If she scored 80 marks and yet failed by 20 marks, then what were the maximum marks?

1) 220

2) 250

3) 300

4) 200

Solution:

Given:

Let maximum marks = x

Passing marks = 40% = 0.4 x → (i)

Marks scored = 80

Remaining marks to pass = 20

Passing marks = 80 + 20 = 100 → (ii)

Equation (i) and (ii),

0.4 x = 100

x = 100 ÷ 0.4

x = 1000 ÷ 4

x = 250

So, the maximum mark is 250. Hence, the second option is correct.

Example:
Directions: The value of a certain product depreciates at the rate of 20% every year. It was purchased 3 years ago. If its present value is INR 10,000, then what was the approximate purchase price of the product?

1) INR 15,237

2) INR 19,531

3) INR 18,145

4) INR 25,000

Solution:

Given:

Let the purchasing value of the product 3 years ago = P

Depreciation rate = 20% every year

Time = 3 years

Equivalent depreciation rate for 3 years –

Equivalent rate for 2 years = (20 + 20) - {(20 × 20) ÷ 100} = 40 – (400 ÷ 100) = 40 – 4 = 36%

Equivalent rate of 36% and 20% = (36 + 20) – {(36 × 20) ÷ 100} = 56 – (720 ÷ 100) = 56 – 7.2 = 48.8%. Thus, the product value has been depreciated by 48.8% in 3 years

Remaining value = 100 – 48.8 = 51.2%
Present value = Rs. 10,000

51.2% of P = (51.2 ÷ 100) × P

Similarly,

51.2% of 10,000 = 10,000 ÷ 0.512 P

= 19531.25 ~ 19531

Thus, the product's value 3 years ago was Rs. 19531. Hence, the second option is correct.

7. Ratio and Proportion Problems in Reasoning

A comparison of two quantities by division is called a ratio and the equality of two ratios is called proportion. A ratio can be represented in different forms such as a : b or a/b whereas the proportion is defined as an equation which says that two ratios are equal. In logical reasoning, one question is seen in various competitive and entrance exams. The basic concept-based questions are asked in the reasoning from this topic.

Definition and Properties of Ratio

Ratio defines the relationship between the quantities of two or more objects. The ratio of two quantities x and y in the same units is the fraction x/y and we write it as x : y.

In the ratio x : y. The first term x is called antecedent and the second term y is called consequent.
Example: The ratio 6 : 7 represents 6/7 with antecedent = 6; Consequent = 7
Note: The multiplication or division of each term of a ratio by the same non-zero number does not affect the ratio.

Proportion is defined as the equality of two ratios. If a : b = c : d, we write it as a : b :: c : d and we say that a, b, c, d are in proportion.
Here a and d are called extremes, while b and c are called mean terms.
The product of the means = The product of the extremes
Therefore, a : b :: c : d and (b x c) = (a x d)

Techniques to solve ratio-related reasoning questions

1) First of all determine the known and the unknown ratio.
2) In the second step set up the proportion or find the value of one part by dividing the comparison value by the number of parts given.
3) Cross-multiply the values and solve.
4) If you want to check the answer you can check by plugging the result into the unknown ratio.

Arithmetic problem solving examples

Example:
Directions: One day, 90 students were travelling in a bus and the ratio of the number of boys to girls was 2: 1. The next day, the number of students remained the same, but the ratio of the number of boys to girls became 3: 2. What was the difference between the numbers of boys travelling in the bus on both the days?

1) 18

2) 6

3) 14

4)30

Solution:

Given:

90 students were travelling in a bus and the ratio of the number of boys to that of girls was 2: 1

According to the question,

2x + x = 90

3x = 90
x = 90 ÷ 3

x = 30

Therefore, Number of Boys = 60, Number of Girls = 30;

The next day, the number of students remained the same, but the ratio of the number of boys to that of girls became 3: 2

3x + 2x = 90

5x = 90

x = 90 ÷ 5

x = 18

Therefore, the Number of Boys = 54, The Number of Girls = 36

So the difference between the numbers of boys travelling in the bus = 60 – 54 = 6

Therefore, the difference between the numbers of boys travelling on the bus on both days is 6. Hence, the second option is correct.

8. Mensuration Problems in Reasoning

Mensuration is defined as the branch of mathematics that studies the measurement of geometric figures and their other parameters such as area, volume, length, breadth, surface area etc. In reasoning basic formula-based questions are asked from this topic. Mostly, 1 - 2 questions are asked in various competitive and entrance exams. You should learn formulae to solve mensuration questions in logical reasoning.

Formulas Related to Mensuration Problems

1) Area of Rectangle = Length x Breadth
2) Perimeter of Rectangle = 2 (Length + Breadth)
3) Area of a square = (side)² = 1/2(diagonal)²
4) Area of walls of a room = 2 (Length + Breadth) x Height
5) Area of a triangle = ½ x Base x Height
6) Area of parallelogram = Base x Height
7) Area of rhombus = ½ x (Product of diagonals)
8) Area of trapezium = ½ x (sum of parallel sides) x distance between them
9) Volume of cuboid = (Length x Breadth x Height) cubic units
10) Surface area of cuboid = 2 (lb + bh + lh) sq.units
11) Volume of cube = a³ cubic units
12) Surface area of cube = 6a² sq.units
(Note: In logical reasoning formulae based questions are asked from this topic. So, you should learn the formulas to attempt the questions easily.)

Arithmetic problems example:
Question: If one side of a square is 6 cm, then what will be its area and perimeter?
Solution:
Given:
Length of side of square = 6 cm
Area = side² = 62 = 36 cm²
Perimeter = Sum of all sides or 4 x side
= 6 + 6 + 6 + 6 = 24 cm

9. Profit and Loss Problems in Reasoning

Profit and Loss are used to identify the price of an article in the market and to determine the profit of a business. Each article has a cost price and a selling price. Based on these you can calculate the profit or loss incurred for a particular article. Profit and Loss are asked in almost all competitive and entrance exams. In the reasoning section formulae based questions are mostly seen in the exams.

Profit and Loss Concepts

1) Cost Price (C.P.) - The price at which the article is purchased is called its cost price
2) Selling Price (S.P.) - The price at which the article is sold is called its selling price.
3) Profit or Gain - If the selling price is greater than the cost price, the seller is said to have a profit or gain.
4) Loss - If the selling price is less than the cost price, the seller is said to have incurred a loss.

Formulae of Profit and Loss

1) Profit/ Gain = S.P - C.P.
2) Loss = C.P. - S.P.
3) Gain% / Profit % = (Gain x 100/ C.P.)
4) Loss % = (Loss x 100 / C.P.)
5) If an article is sold at a profit of 25% then S.P. = 125% of C.P.
6) If an article is sold at a loss of 25% then S.P. = 75% of C.P.
7) S.P. =(100+Gain%)100× C.P.
8) S.P. =(100− Loss %)100× C.P.
9) C.P. =100(100+Gain%)× S.P.
10) C.P. =100(100−Loss%)× S.P.

Example:
Directions: A man bought 30 defective machines for INR 1,000. He repaired and sold them at a rate of INR 300 per machine. He made a profit of INR 150 per machine. How much did he spend on repairs?

1) INR 5,500
2) INR 4,500
3) INR 3,500
4) INR 2,500

Solution:
Use the formula:

Repair cost = selling price – profit – cost price.

The cost price of 30 defective machines = INR 1,000

The selling price of 1 machine = INR 300

Total selling price = INR 300 × 30 = INR 9,000

Profit per machine = INR 150

Total profit = INR 150 × 30 = INR 4,500

Repair cost = selling price – profit – cost price.

= 9,000 – 4,500 – 1,000

= INR 3,500

Hence, the correct answer is INR 3,500.

Arithmetic Questions with Answers

1) Directions: A man was 32 years of age when he had his first son. His wife was 35 years of age when his son attained the age of 7 years. The difference in age between the man and his wife is?

1) 7 years

2) 3 years

3) 5 years

4) 4 years

Solution:

According to the question –

The age of the wife when her son was born was (35 – 7) = 28 years

But, the age of the man was 32 years old when his son was born.

Therefore, the difference in age between the man and his wife is (32 – 28) = 4 years.

So, the difference in age between the man and his wife is 4 years. Hence, the fourth option is correct.

2) Directions: Hari is twice as old as Johnny, who is three years older than Rahul. If Hari's age is five times Rahul's age, how old is Johnny?

1) 2 years

2) 4 years

3) 5 years

4) 8 years

Solution:

Let the ages of Hari, Johnny, and Rahul be H, J, and R respectively.

Hari is twice as old as Johnny ⇒ H = 2 × J (1st equation)

Johnny is three years older than Rahul ⇒ R + 3 = J

⇒ R = J – 3 (2nd equation)

Hari's age is five times Rahul's age ⇒ H = 5 × R (3rd equation)

Putting the value of R from the second equation in the above equation, the equation becomes –

⇒ H = 5 × (J – 3)

But, H = 2 × J (1st equation)

So, 5 × (J – 3) = 2 × J

⇒ 5 × J – 15 = 2 × J

⇒ 3 × J = 15

⇒ J = 5

So, the age of Johnny is 5 years. Hence, the third option is correct.

3) Directions: A father's age is one more than 5 times his son's age. After 3 years, the father's age would be 2 less than four times the son's age. Find the present age of the father.

1) 30 years

2) 40 years

3) 31 years

4) 29 years

Solution:

Let the present age of the father and son be F and S years respectively.

The father's present age is 1 more than 5 times his son's age ⇒ F = (5 × S) + 1

Father's age after 3 years = (5 × S) + 4

Son's age after 3 years = S + 3

After 3 years, the father's age would be 2 less than four times the son's age.

⇒ (5 × S) + 4 = 4 × (S + 3) – 2

⇒ (5 × S) + 4 = (4 × S) + 12 – 2 = (4 × S) + 10

⇒ S = 6

⇒ F = (5 × S) + 1

= 5 × 6 + 1 = 30 + 1 = 31 years.

So, the present age of the father is 31 years. Hence, the third option is correct.

4) Directions: The average age of 19 boys in a class is 21 years. If the teacher's age is included, the average increases to 22 years. What is the teacher's age?

1) 39 years

2) 41 years

3) 40 years

4) 44 years

Solution:

Given:

The average age of 19 boys in a class is 21 years.

Average⇒(Sum of ages of 19 boys) ÷ 19 = 21

So, the sum of the ages of 19 boys = 19 × 21 = 399

The average age of 19 boys and the teacher is 22 years.

Average (including teacher's age)⇒(Sum of ages of 19 boys + Age of the teacher) ÷ 20 = 22

⇒(Sum of ages of 19 boys + Age of the teacher) = 22 × 20 = 440

Substitute the sum of the ages of 19 boys by 399 (calculated above)

⇒399 + (Age of the teacher) = 22 × 20 = 440

⇒Age of the teacher = 440 – 399 = 41 years

So, the age of the teacher is 41 years. Hence, the second option is correct.
5) Directions: In a family, Mr. Prakash has his wife and his two married brothers of whom one has two children and another has no child. How many members are there in the family?

1) 12 members

2) 8 members

3) 6 members

4) 10 members

Solution:

Mr. Prakash and his wife constitute 2 members.

Mr. Prakash has two married brothers. These constitute 4 members (His 2 brothers and their wives).

Also, one of the two married brothers has two children. These constitute 2 members.

So, the total members in the family are 2 + 4 + 2 = 8
Hence, the second option is correct.

6) Directions: Two persons A and B get the same salary. Their basic pay is different. The allowances are 65% and 80% of the basic pay respectively. What is the ratio of the basic pay?

1) 17 : 15

2) 7 : 5

3) 11 : 10

4) 12 : 11

Solution:

Given:

Two persons A and B get the same salary.

Their basic pay is different.

The allowances are 65% and 80% of the basic pay respectively.

Let's consider that A's basic pay is X and B's is Y.

As per the given details,

Allowances of A = 65% of basic pay

Salary of A = X + 65% of X

⇒ X + (65 ÷ 100) × X

⇒ X + (65X) ÷ 100

⇒ (100X + 65X) ÷ 100

⇒ 165X ÷ 100

Allowances of B = 80% of basic pay

Salary of B = Y + 80% of Y

⇒ Y + (80 ÷ 100) × Y

⇒ Y + (80Y) ÷ 100

⇒ (100 + 80Y) ÷ 100

⇒ 180Y ÷ 100

Again, it is given that both salaries are equal.

Therefore,

165X ÷ 100 = 180Y ÷ 100

⇒ 165X = 180Y (cancelling 100 on both sides denominators)

⇒ X ÷ Y = 180 ÷ 165

⇒ X : Y = 180 : 165

⇒ X : Y = 12 : 11

So, the ratio of the basic pay is 12 : 11. Hence, the fourth option is correct.

7) Directions: Six regular hexagons of side 5 cm are joined together to form the figure given below. What is the perimeter of the figure?

1) 210

2) 180

3) 120

4) 240
Solution:

Given:

The side of a regular hexagon is 5cm.

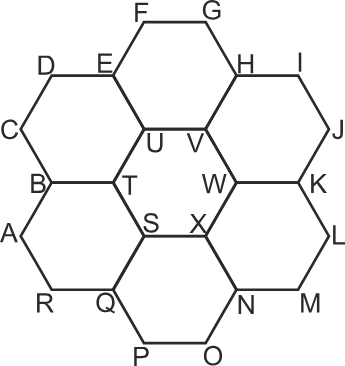
The perimeter of a given figure(P) = (Total length of the external boundary) + (Total length of the internal boundary)

P = (AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LM + MN + NO + OP + PQ + QR + RA) + (ST + TU + UV + VW + WX + XS)

P = (5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5) + (5 + 5 + 5 + 5 + 5 + 5)

P = 90 + 30

P = 120

Therefore, 120 is the perimeter of the given figure. Hence, the third option is correct.

8) Directions: If in a business, Alok gains 75% more profit than Akash, then by what percentage profit of Akash is less than the profit of Alok?

1) 25%

2) 12.63%

3) 30.8%

4) 42.85%

Solution:

Given:

In a business, Alok gains 75% more profit than Akash.

Let us assume that Akash makes a profit of ₹ 100

The profit of Alok is 75% more than Akash.

Hence, profit of Akash = 100 + (75/100 × 100) = 100 + 75 = 175

So, profit earned by Alok over Akash = 175 – 75 = 75

% Profit earned by Alok over Akash = {(more profit earned by Alok) / total profit earned by Alok } × 100

= [(75 ÷ 175) × 100] %

= 0.42857 × 100%

= 42.85 %

Therefore, Akash earns 42.85% less profit than Alok. Hence, the fourth option is correct.

9) Directions: A total of 60 students are travelling in a bus. The ratio of the number of boys to that of girls is 2 : 1. Then, 15 boys get down 5 girls get on the bus at the first stop, 5 boys get in and 10 girls get down from the bus at the second stop. What is the ratio of the number of boys to that of girls in the bus after the second stop?

1) 3 : 2

2) 2 : 1

3) 2 : 3

4) 3 : 1

Solution:

Given:

A total of 60 students are travelling in a bus. The ratio of the number of boys to that of girls is 2 : 1

2x + x = 60; 3x = 60; x = 60 ÷ 3; x = 20

Thus, Number of Boys = 2x = 40; Number of Girls = x = 20

Then, 15 boys get down and 5 girls get on the bus at the first stop

The remaining boys after the first stop; 40 – 15 = 25

The remaining girls after the first stop; 20 + 5 = 25

At the second stop, 5 boys get in and 10 girls get down from the bus.

The remaining boys after the second stop; 25 + 5 = 30

The remaining girls after the second stop; 25 – 10 = 15

So, the ratio of Boys: Girls = 30 : 15; 2 : 1. Hence, the second option is correct.

10) Directions: The sum of a number's square, its cube, and its next number's cube is 205. What is the number?

1) 3

2) 5

3) 4

4) 6

Solution:

Given:

x² + x³ + (x + 1)³ = 205
By using the above equation let's check the option –

First option: 3; 3² + 3³ + (3 + 1)³ = 9 + 27 + 64 = 100 ≠ 205

Second option: 5; 5² + 5³ + (5 + 1)³ = 25 + 125 + 216 = 366 ≠ 205

Third option: 4; 4² + 4³ + (4 + 1)³ = 16 + 64 + 125 = 205

Fourth option: 6; 6² + 6³ + (6 + 1)³ = 36 + 216 + 343 = 595 ≠ 205

So, the sum of the 4's square, its cube, and its next number's cube is 205. Hence, the third option is correct;

11) Directions: When a number is added to its next number and another number that is four times its next number, the sum of these three numbers is 95. Find the number.

1) 16

2) 14

3) 17

4) 15

Solution:

Let, the number be x

According to the question –

x + (x + 1) + 4(x + 1) = 95

By solving the above equation –

6x + 5 = 95

6x = 95 – 5

6x = 90

x = 90 ÷ 6 = 15

So, the number is 15. Hence, the fourth option is correct.

12) Directions: A man bought 25 crates of oranges for INR 10,000. He lost five crates. In order to earn a total profit of 25% of the total cost, he would have to sell each of the remaining crates at:

1) INR 650

2) INR 625

3) INR 600

4) INR 575

Solution:

The cost price of 25 crates of oranges = INR 10,000

Total profit = 25% of total cost = 25% of INR 10,000 = INR 2,500

The selling price of 25 crates of oranges = cost price + total profit

= INR 10,000 + INR 2,500

= INR 12,500

Number of crates of oranges sold = 25 – 5 = 20

⇒ Selling price per crate = 12,500/20 = INR 625

Hence, the correct answer is INR 625.

13) Directions: A rides his bicycle at 15 km/hr, while B starts his ride after 6 hours to catch A at a speed of 25 km/hr. Time taken by B to catch A (in hours) is:

1) 9

2) 8

3) 10

4) 6

Solution:

Distance travelled by A = Speed × Time

So, Distance = 15 × 6 = 90 km

Relative speed of B to A = Speed of B – Speed of A

Relative speed = (25 – 15) km/hr = 10 km/hr

Time taken by B to catch A = Distance/ Relative Speed

= 90/10 = 9 hours

Hence, the correct answer is 9.

14) Directions: A thief steals a bike at 12:30 p.m. and drives it at 48 km/hr. But the theft is discovered after half an hour. The bike owner starts to chase him on another bike at 58 km/hr. The thief will be caught at ________.

1) 3:40 p.m.

2) 3:54 p.m.

3) 3:10 p.m.

4) 3:24 p.m.

Solution:

Speed of thief = 48 km/hr

Distance travelled by him in 30 mins = 48 x 30/60 = 24km

Owner speed = 58 km/hr

Their relative speed = 58 – 48 = 10 km/hr

Time = Distance/ Speed = 24/10 = 2 hours 24 minutes

The owner started after 30 minutes at 1:00 p.m.

The thief gets caught at 1:00 + 2:24 = 3:24 p.m.

Hence, the correct answer is 3:24 p.m.

15) Directions: What is the value of x?

If x = 0.05 × 0.36 ÷ 0.4 + 0.055 + 1.50 ÷ 0.03

1) 45.9

2) 50.1

3) 55.1

4) 49.9

Solution:

x = 0.05 × 0.36 ÷ 0.4 + 0.055 + 1.50 ÷ 0.03

⇒ x = 0.05 × 0.9 + 0.055 + 50

⇒ x = 0.045 + 0.055 + 50

⇒ x = 50.1

Hence, the correct answer is 50.1

16) Directions: What is the value of 2160 × 3 ÷ 144 + 13 - 2?

1) 56
2) 57
3) 59
4) 54

Solution:

Follow the BODMAS Rule

B = Brackets; O= Of; D= Division; M= Multiplications; A= Addition; S= Subtraction.

Using the BODMAS Rule,

2160 × 3 ÷ 144 + 13 - 2

= 2160 × 3/144 +13 - 2

= 15 × 3 + 11

= 45 + 11 = 56

Hence, the correct answer is 56.

17. Directions: Sonu and his friend Rahul went shopping. Sonu had Rs. 500 with him while Rahul had Rs. 240. Sonu spent twice as much as Rahul on shopping. Now Sonu has three times as much money as is left with Rahul. How much money did Sonu spend?

1) Rs. 60

2) Rs. 440

3) Rs. 120

4) Rs. 220

Solution:

Given:

Sonu had = Rs. 500

Rahul had = Rs. 240

Let the money spent by Rahul on shopping be x.

So, Sonu spent the money on shopping is 2x.

According to the question,

(500 – 2x) = 3(240 – x)

(500 – 2x) = (720 – 3x)

(3x – 2x) = (720 – 500)

x = 220

The money spent by Sonu on shopping is 2x, 2 × 220 = Rs. 440. Hence, the second option is correct.

18. Directions: If a train 150 m long crosses a pole in 12 seconds, then what is the speed of the train in km/h?

1) 45

2) 60

3) 50

4) 75

Solution:

Given:

Length of a train = 150m

Time taken to cross the pole = 12sec

So, Speed = Distance ÷ Time

= 150 ÷ 12 = 25/2 m/sec = 45 km/h

So, 45 km/h is the required answer. Hence, the first option is correct.

19. Directions: In a zoo, there are Rabbits and Pigeons. If heads are counted, there are 200 and if legs are counted, there are 580. How many pigeons are there?
1) 90

2) 100

3) 110

4) 120

Solution

Given:

Total number of legs = 580

Total number of heads = 200

Let the number of pigeons is X and the number of rabbits is Y.

Total number of heads = 200

⇒ X + Y = 200→(1)

We know that a rabbit has 4 legs and a pigeon has 2 legs.

⇒ 2X + 4Y = 580 or X + 2Y = 290→(2)

By solving equations (1) and (2)

X = 290 – 2Y

(290 – 2Y) + Y = 200

⇒ Y = 90

Also X + Y = 200

⇒ 90 + X = 200

⇒ X = 110

So, the number of pigeons is 110. Hence, the third option is correct.

20. Directions: If 10 boys walk 10 km in 10 days, then how many days it will take for 3 boys to walk 10 km?

1) 33.33

2) 36

3) 66.66

4) 10

Solution:

Given:

M1 = 10; W1 = 10; D1 =10

M2 = 3; W2 = 10; D2 = ?

Here, M→boys; W→work done; D→days

Therefore, (M1 × D1) ÷ W1 = (M2 × D2) ÷ W2

⇒ (10 × 10) ÷ 10 = (3 × D2) ÷ 10

⇒ 100 = 3 × D2

⇒ D2 = 100/3

⇒ D2 = 33.33 days

So, the number of days is 33.33. Hence, the first option is correct.

Learn more: The verbal reasoning topics given below.

Arithmetical Problems for SSC MTS/ SSC CHSL/ SSC Stenographer/ RRB exams

1) Directions: Sumit wants to get his clothes washed. The laundry service charges in his city are such that for the first kg. of clothes, he is charged Rs 150, and after that, he is charged Rs 50 for every kg that follows. If he gets 10 kg of clothes washed, how much money does he pay for the laundry service?

1) Rs 250

2) Rs 450

3) Rs 650

4) Rs 600

Hint: Determine the total cost of washing by adding the cost of washing 1 kg and the remaining 9 kg of clothes at given rates.

Solution

Given:

The weight of clothes that Sumit wants to get washed = 10kg

The cost of washing the first kg of clothes = Rs. 150

The cost of the remaining 9 kg of clothes = 50 × 9 = 450

The total cost of washing is 450 + 150 = 600

So, the total cost of washing is Rs. 600. Hence, the fourth option is correct.

2) Directions: The present ages of Ankur and his sister are in the ratio of 4:3. After 6 years, the ratio of Ankur's sister and brother will be 3:2. If the present age of his brother is 32 years, what will be the age (in years) of Ankur after 3 years?

1) 71

2) 68

3) 70

4) 65

Hint: First, assume Ankur's brother's current age is 2A and compare it to the given age to determine the unknown. Then, use ratios to calculate Ankur's age in 3 years from the present.

Solution

Given:

The present age of Ankur's brother is 32 years.

⇒ His age 6 years later = 38 years

But, after 6 years the ratio of ages of Ankur's sister and brother will be 3:2.

After 6 years, Ankur's sister's age = 3A, Ankur's brother's age = 2A

⇒ 2A = 38

⇒ A = 38 ÷ 2 = 19

⇒ Ankur's sister's age 6 years later = 57 years

⇒ Ankur's sister's present age→57 – 6 = 51 years

But, the present ages of Ankur and his sister are in the ratio of 4:3.

Ankur's sister's present age = 3A, Ankur's present age = 4A

⇒ Ankur's sister's present age→57 – 6 = 51 years

⇒ 3A = 51

⇒ A = 51 ÷ 3 = 17

⇒ Ankur's present age = 4 × 17 = 68 years

Ankur's age after 3 years will be 71 years. Hence, the first option is correct.

For more practice you must download the e-book of Arithmetic problems with solutions PDF below:
Arithmatical Problems Questions with Solutions PDF

Arithmetical Problems for IBPS RRB Assistant/ IBPS CWE Clerical/ Insurance Assistant exams

1) Directions: Joel and Tom were travelling from town X to town Y which was 210 km apart. Joel set off 1 hour and 15 minutes later than Tom but arrived 15 minutes earlier. If the average speed of Tom was 42 km/h, find the average speed of Joel.

1) 50 km/h

2) 60 km/h

3) 65 km/h

4) 70 km/h

Hint: Solve, using the formulae of speed and time to get the required answer.

Solution

Given:

Distance between town X and town Y = 210 km

Average speed of Tom = 42 km/h

Time taken by Tom = Distance ÷ Speed

= 210 ÷ 42

= 5 hours

Here, Joel started 1hr 15 mins late and arrived 15 mins earlier.

Thus, the time taken by Joel

= 5 hrs – 1hr 15mins – 15mins

= (5 × 60) – (1 × 60 + 15) – 15

= 300 – 75 – 15

= 300 – 90

= 210 mins

Now, convert minutes into hours –

= 210 ÷ 60

= 3.50 hrs

Average speed = Distance ÷ Time

= 210 ÷ 3.5

= 60 km/h

So, the average speed of Joel is 60 km/h. Hence, the second option is correct.

2) Directions: Ravi had five subjects in his final examination. The maximum marks in each subject are 100. If his percentage in four subjects is 80, and he scores 65 marks in the fifth subject, determine his overall percentage for the five subjects.

1) 0.78

2) 0.79

3) 0.77

4) 0.76

Hint: Determine the marks of five subjects scored by Ravi from the given information and calculate the percentage.

Solution

Given:

Total number of Subjects→5

Maximum marks in each subject→100

% scored by Ravi in 4 subjects = 80%

Marks scored by Ravi in the 5th subject = 65

From the given information –

Maximum marks in all 5 subjects = 100 × 5 = 500

% scored by Ravi in 4 subjects = 80%

Total marks scored by Ravi in 4 subjects = 80/100 × (100 × 4)

= 80/100 x 400

= 320

Therefore, the total marks scored by Ravi in all 5 subjects = 320 + 65 = 385

⇒ Total % scored by Ravi = (385/500 × 100) % = 77% = 0.77

Hence, the third option is correct.

Read more: The important non verbal reasoning topics are given below:

About the Faculty
Tanu Gupta, with over a decade of experience as a reasoning faculty, specializes in preparing students for various entrance examinations and career development. Her extensive work with multiple educational platforms and institutions has honed her expertise in logical and analytical thinking. Her dedication to innovative teaching methods ensures these articles provide practical insights and expert guidance.