Binary Logic: Meaning, Reasoning Questions with Answers, Examples

Binary logic is a collection of statements and people state these statements. It is the collection of rules or methods for determining whether the statement is true or false. In binary logic reasoning, we have three types of operations AND, OR, and NOT. An aspirant needs to observe the statements carefully and then decide which statements are true or false. Binary logic reasoning questions are mostly seen in the UGC NET, CAT, CLAT etc. exams.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: IBSAT 2024 Mock Tests | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

Question with Solutions: Missing Number | Alphabet Test | Arithmatical Problems | Calendar

This Story also Contains

1. Type of persons in binary logic reasoning
2. Binary Logic and Boolean Algebra
3. Types Binary Logic Reasoning Questions
4. Truth-Tellers and Liars Problems
5. Question Weightage of Binary Logic in Competitive Exams
6. Binary Logic Reasoning CAT Questions for Practice
7. Binary Logic Reasoning Questions for UPESMET/ JIPMAT
8. Binary Logic Reasoning Questions for CAT/ XAT/ MAT

Type of persons in binary logic reasoning

According to the statement stated by people, we can divide people into three categories in binary logic reasoning according to their statements.

Types of Persons

1. True Teller

2. Liar

3. Alternator

Let’s understand these types of persons in detail -

1. True Teller -

A true teller always speaks the truth. Every statement of a truth-teller is true.

2. Liar -

A liars always speak lies. Every statement of the liar is always false.

3. Alternator -

An alternator is a person who always tries to manipulate the statements. An alternator always tries to convert true statements into false and false statements to true.

Binary Logic and Boolean Algebra

As we know binary logic works on the values of true or false whereas boolean algebra is the type of algebra that works on the values 0 or 1. Here, 1 denotes True and 0 denotes false values. Three important types of operations are performed on boolean algebra called conjunction (∧), disjunction (∨) and negation (¬). Conjunction means AND, Disjunction means OR and Negation denotes NOT.

Boolean Algebra Operations

1. Conjunction or AND operation

2. Disjunction or OR operation

3. Negation or Not operation

Types Binary Logic Reasoning Questions

There are two types of questions asked in the exam on this topic.
Note: Binary logic examples are given with each question type.

Question Type 1

In this type of question, three persons stated six statements each person stated two statements where one statement is true and one false.

Example

Sam, Ram and Max participated in a game and one of them won the game. They belong to three different communities - A, B and C. A community always speak the truth, B community always lies and C community tells the truth and lies alternatively. (Each of Sam, Ram and Max belongs to one community.) After the game, they gave these statements.

Sam:

I would have won the game if Max had not obstructed me at the last moment.

Max always speaks the truth.

Ram:

Sam won the race.

Max does not belong to the B community.

Max:

I hadn’t obstructed Sam at the last moment.

Ram won the game.

Max belongs to which community?

1. A

2. B

3. C

4. Either 2 or 3

Solution:

Assume Ramis is a truth-teller (So, he belongs to A community). Then Sam is the winner and Max belongs to the C community (Alternator) which implies Sam is a liar (B).

If we check the truthfulness of Sam, we get that both his statements are wrong and Max's one statement is wrong. So, Max belongs to C and Sam won the game.

Question Type 2

In this type of question, if two types of persons are there where one person always speaks the truth and the other always tells a lie.

Example

Three persons P, Q and R gave these statements:

P said, either the Red Party or BlueParty won the elections.

Q said the Red Party won.

R said neither the Red Party nor the Blue Party won the elections.

Of these persons, only one person is wrong.

Who won the elections?

1. Red Party

2. Blue Party

3. Data Inadequate

4. None of these

Solution

As only one person is wrong, Therefore, two persons are right. Assume that the Red Party won the election. So, the statements of P and Q are true as they satisfy our condition that 2 of them are truth-tellers. Therefore, the Red Party wins the election.

If you assume that the Blue Party won the election, statements of Q and R become false that is violating the given condition.

Truth-Tellers and Liars Problems

Truth-tellers and liars problems is a logical puzzle and it is also called the Knights and Knaves problem. In this type of question or puzzle, a sequence of statements is given in which some are true and some are false. Based on these statements an aspirant has to determine the true statements.

Example

Chris and Bob are in the garden.

Bob says: "If 48 is odd, then I am a truth-teller."
Chris says: "Bob is a liar."

Determine whether each person is a truth-teller or a liar.

Solution

As we know 48 is not an odd number, the "if" part of Bob's statement is false. Hence, Bob's statement is true. Therefore, Bob must be a truth-teller.

Now, Chris says "Bob is a liar", and that is false since I just showed that Bob is a truth-teller. Therefore, Chris is a liar.

Hence, Phoebe is a truth-teller and Calvin is a liar.

Question Weightage of Binary Logic in Competitive Exams

Binary logic is asked in CAT and CLAT exams and the weightage is 3 to 5 questions. As it is one of the important chapter you should practice various binary logic reasoning pdf. There are many binary logic reasoning questions pdf available online.
For more CAT and CLAT topics you must refer the below table:

Binary Logic Reasoning CAT Questions for Practice

1. Directions: In an institute, there are three top rankers in a batch, Karthik, Waheeda, and Ritesh, not necessarily in the same order, who made the following statements about their ranks.

Karthik: (A) I am not the top ranker.

(B) Waheeda is not the second ranker.

(C) Ritesh is the third ranker.

Waheeda: (A) Karthik’s first statement is false.

(B) I am the third ranker.

(C) I made two false statements.

Ritesh: (A) Karthik is the first ranker.

(B) Waheeda is not the second ranker.

(C) I am the second ranker.

It is known that each of Karthik and Ritesh made only one false statement. Waheeda made only one true statement.

Question: Who is the first ranker?

1) Karthik

2) Waheeda

3) Ritesh

4) Cannot be determined

Solution

It is given that Waheeda made only one true statement. It implies that she made two false statements.

⇒ Waheeda’s third statement is true and the other two are false.

⇒ Karthik’s first statement is true. (From Waheeda’s first statement) i.e. Karthik is not the top ranker.

⇒ Ritesh’s first statement is false and the other two are true.

⇒ Ritesh is the second ranker and Waheeda is not the second ranker. As Karthik is not the first ranker, Waheeda is the first ranker and Karthik is the third ranker.

⇒ Karthik’s second statement is true and the third one is false.

Therefore, the arrangement is as follows:

Waheeda > Ritesh > Karthik

So, Waheeda is the first ranker. Hence, the second option is correct.

2. Directions: In an institute, there are three top rankers in a batch, Karthik, Waheeda, and Ritesh, not necessarily in the same order, who made the following statements about their ranks.

Karthik: (A) I am not the top ranker.

(B) Waheeda is not the second ranker.

(C) Ritesh is the third ranker.

Waheeda: (A) Karthik’s first statement is false.

(B) I am the third ranker.

(C) I made two false statements.

Ritesh: (A) Karthik is the first ranker.

(B) Waheeda is not the second ranker.

(C) I am the second ranker.

It is known that each of Karthik and Ritesh made only one false statement. Waheeda made only one true statement.

Question: Which of the following represents the correct order of truth and false statements made by Karthik?

1) True, False, True

2) True, True, False

3) False, True, True

4) Cannot be determined

Solution

It is given that Waheeda made only one true statement. It implies that She made two false statements.

⇒ Waheeda’s third statement is true and the other two are false.

⇒ Karthik’s first statement is true. (From Waheeda’s first statement) i.e. Karthik is not the top ranker.

⇒ Ritesh’s first statement is false and the other two are true.

⇒ Ritesh is the second ranker and Waheeda is not the second ranker. As Karthik is not the first ranker, Waheeda is the first ranker and Karthik is the third ranker.

⇒ Karthik’s second statement is true and the third one is false.

Therefore, the correct order of truth and false statements made by Karthik are true, true false. Hence, the second option is correct.

3. Directions: In an institute, there are three top rankers in a batch, Karthik, Waheeda, and Ritesh, not necessarily in the same order, who made the following statements about their ranks.

Karthik: (A) I am not the top ranker.

(B) Waheeda is not the second ranker.

(C) Ritesh is the third ranker.

Waheeda: (A) Karthik’s first statement is false.

(B) I am the third ranker.

(C) I made two false statements.

Ritesh: (A) Karthik is the first ranker.

(B) Waheeda is not the second ranker.

(C) I am the second ranker.

It is known that each of Karthik and Ritesh made only one false statement. Waheeda made only one true statement.

Question: Who is the third ranker?

1) Karthik

2) Waheeda

3) Ritesh

4) Cannot be determined

Solution

It is given that Waheeda made only one true statement. It implies that She made two false statements.

⇒ Waheeda’s third statement is true and the other two are false.

⇒ Karthik’s first statement is true. (From Waheeda’s first statement) i.e. Karthik is not the top ranker.

⇒ Ritesh’s first statement is false and the other two are true.

⇒ Ritesh is the second ranker and Waheeda is not the second ranker. As Karthik is not the first ranker, Waheeda is the first ranker and Karthik is the third ranker.

⇒ Karthik’s second statement is true and the third one is false.

Therefore, the arrangement is as follows:

Waheeda > Ritesh > Karthik

Therefore, Karthik is the third ranker. Hence, the first option is correct.

4. Directions: In an institute, there are three top rankers in a batch, Karthik, Waheeda, and Ritesh, not necessarily in the same order, who made the following statements about their ranks.

Karthik: (A) I am not the top ranker.

(B) Waheeda is not the second ranker.

(C) Ritesh is the third ranker.

Waheeda: (A) Karthik’s first statement is false.

(B) I am the third ranker.

(C) I made two false statements.

Ritesh: (A) Karthik is the first ranker.

(B) Waheeda is not the second ranker.

(C) I am the second ranker.

It is known that each of Karthik and Ritesh made only one false statement. Waheeda made only one true statement.

Question: If Waheeda’s statements are not considered, which of the following represents the correct order of truth and false statements made by Ritesh so that the rank of all three will not alter?

1) True, False, True

2) True, True, False

3) False, True, True

4) Cannot be determined

Solution

It is given that Waheeda made only one true statement. It implies that She made two false statements.

⇒ Waheeda’s third statement is true and the other two are false.

⇒ Karthik’s first statement is true. (From Waheeda’s first statement) i.e. Karthik is not the top ranker.

⇒ Ritesh’s first statement is false and the other two are true.

⇒ Ritesh is the second ranker and Waheeda is not the second ranker. As Karthik is not the first ranker, Waheeda is the first ranker and Karthik is the third ranker.

⇒ Karthik’s second statement is true and the third one is false.

Therefore, the arrangement is as follows:

Waheeda > Ritesh > Karthik

If Waheeda’s statements are not considered, then the correct order of truth and false statements made by Ritesh are False, true, and true. Hence, the third option is correct.

5. Directions: In an institute, there are three top rankers in a batch, Karthik, Waheeda, and Ritesh, not necessarily in the same order, who made the following statements about their ranks.

Karthik: (A) I am not the top ranker.

(B) Waheeda is not the second ranker.

(C) Ritesh is the third ranker.

Waheeda: (A) Karthik’s first statement is false.

(B) I am the third ranker.

(C) I made two false statements.

Ritesh: (A) Karthik is the first ranker.

(B) Waheeda is not the second ranker.

(C) I am the second ranker.

It is known that each of Karthik and Ritesh made only one false statement. Waheeda made only one true statement.

Question: Which statement of Karthik and Ritesh is True?

1) 1

2) 2

3) 3

4) None

Solution

It is given that Waheeda made only one true statement. It implies that she made two false statements.

⇒ Waheeda’s third statement is true and the other two are false.

⇒ Karthik’s first statement is true. (From Waheeda’s first statement) i.e. Karthik is not the top ranker.

⇒ Ritesh’s first statement is false and the other two are true.

⇒ Ritesh is the second ranker and Waheeda is not the second ranker. As Karthik is not the first ranker, Waheeda is the first ranker and Karthik is the third ranker.

⇒ Karthik’s second statement is true and the third one is false.

Therefore, statement 2 is true of Karthik and Ritesh. Hence, the second option is correct.

6. Directions: The police rounded up Aman, Ram and Paran yesterday because one of them was suspected of robbing the local bank. The 3 suspects gave the following statements after intensive questioning:

Aman: I’m innocent.

Ram: I’m innocent.

Paran: Ram is the guilty one.

Question: Who robbed the bank among the three persons, if only one of the statements will be true?

1. Ram

2. Aman

3. Param

4. None of these

Solution
Suppose Ram is the robber therefore, Aman is correct. But the statement given by Ram is wrong and Param is also correct as he is pointing towards Ram as the robber. So, 2 statements are correct which is the violation of the given condition.

Now let us assume that Aman is the robber. Then we can see that except for Ram’s statement, the remaining two statements become false. So Aman is the robber.

7. Directions: While Balbir had his back turned, a dog ran into his butcher shop, snatched a piece of meat off the counter and ran out. Balbir was mad when he realised what had

happened. He asked three other shopkeepers, who had seen the dog, to describe it. The shopkeepers didn't want to help Balbir. So each of them made a statement which contained one truth and one lie.

A. Shopkeeper Number 1 said: "The dog had black hair and a long tail."

B. Shopkeeper Number 2 said: "The dog has a short tail and wore a collar."

C. Shopkeeper Number 3 said: "The dog had white hair and no collar."

Based on the above statements, which of the following could be a correct description?

(a) The dog had white hair, a short tail and no collar.

(b) The dog had white hair, a long tail and a collar.

(c) The dog had black hair, a long tail and a collar.

(d) The dog had black hair, a long tail and no collar.

Solution

According to the statement of shopkeeper 1, The dog had black hair and a long tail.

Therefore option (3) and (4) are incorrect.

According to the statement of Shopkeeper 3, The dog had white hair and no collar.

Therefore, option (1) is incorrect.

Hence, the second option is correct.

8. Direction: In each of the following sentences, the main statement is followed by four sentences each. Select a pair of sentences that relate logically to the given statement.

Either Sam is ill, or he is drunk.

A. Sam is ill.

B. Sam is not ill.

C. Sam is drunk.

D. Sam is not drunk.

(a) AB

(b) DA

(c) AC

(d) CD

Solution

According to the statements, Either Sam is ill, or he is drunk so, only Sam is not drunk, so he must be ill are true.

Hence, the second option is correct.

Binary Logic Reasoning Questions for UPESMET/ JIPMAT

Directions: Q (1-4) Students in a college are discussing two proposals -

A: a proposal by the authorities to introduce dress code on campus, and

B: a proposal by the students to allow multinational food franchises to set up outlets on college campus.

A student does not necessarily support either of the two proposals.

In an upcoming election for student union president, there are two candidates in fray:

Sunita and Ragini. Every student prefers one of the two candidates.

A survey was conducted among the students by picking a sample of 500 students. The following information was noted from this survey.

1. 250 students supported proposal A and 250 students supported proposal B.

2. Among the 200 students who preferred Sunita as student union president, 80% supported proposal A.

3. Among those who preferred Ragini, 30% supported proposal A.

4. 20% of those who supported proposal B preferred Sunita.

5. 40% of those who did not support proposal B preferred Ragini.

6. Every student who preferred Sunita and supported proposal B also supported proposal A.

7. Among those who preferred Ragini, 20% did not support any of the proposals.

Q -1) How many of the students surveyed supported proposal B, did not support proposal A and preferred Ragini as student union president?

1) 150

2) 210

3) 200

4) 40

Solution

We can represent the preferences of students who like Sunita and Ragini as disjoint sets in a Venn diagram:

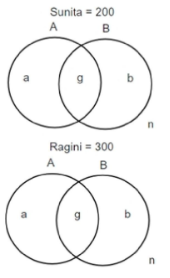
Given: There are a total of 500 students in the survey.

From statement (2),
the number of students who prefer Sunita (S) is 200. Hence, the number of students who prefer Ragini (R) is 500 - 200 = 300.

From statement (1),
A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.

From statement (2),
the number of students who prefer Sunita and support Proposal A (A(S)) is 80% of 200, which is 160.

=> A (Sunita) = 160.

=> A (Ragini) = 90.

From statement (4),
20% of the total 250 students who support Proposal B prefer Sunita

=> B (Sunita) = 20 % of 250 = 50.

=> B (Ragini) = 200.

From statement (6),
=> g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110.

=> n (Sunita) = 40.

From statement (7),

=> n (Ragini) = 60

Now, it is given that 250 students support the proposal B

=> hence the other 250 students do not support proposal B.

From statement (5),

(a + n) of Ragini

= 40 % of 250

= 100.

Hence, a (Ragini) = 40.

Based on the above findings, the below Venn Diagram can be prepared:

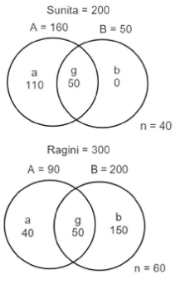
From the diagram, we can understand that option A is correct.

The students who supported proposal B but not A are b (Sunita) and b (Ragini).

Among them those supported Ragini are b (Ragini) = 150.

Hence, the first option is correct.

Q-2) What percentage of the students surveyed who supported both proposals A and B preferred Sunita as student union president?

1) 40

2) 25

3) 20

4) 50

Solution

We can represent the preferences of students who like Sunita and Ragini as disjoint sets in a Venn diagram:

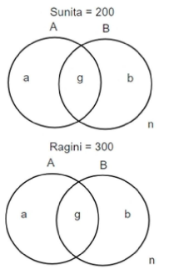
Given: There are a total of 500 students in the survey.

From statement (2),

the number of students who prefer Sunita (S) is 200. Hence, the number of students who prefer Ragini (R) is 500 - 200 = 300.

From statement (1),

A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.

From statement (2),

the number of students who prefer Sunita and support Proposal A (A(S)) is 80% of 200, which is 160.

=> A (Sunita) = 160.

=> A (Ragini) = 90.

From statement (4),

20% of the total 250 students who support Proposal B prefer Sunita

=> B (Sunita) = 20 % of 250 = 50.

=> B (Ragini) = 200.

From statement (6),

=> g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110.

=> n (Sunita) = 40.

From statement (7),

=> n (Ragini) = 60

Now, it is given that 250 students support the proposal B

=> hence the other 250 students do not support proposal B.

From statement (5),

(a + n) of Ragini

= 40 % of 250

= 100.

Hence, a (Ragini) = 40.

Based on the above findings, the below Venn Diagram can be prepared:

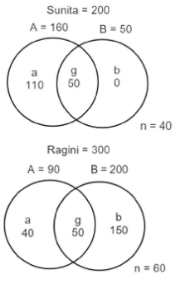
According to the Venn diagram,

the students surveyed who supported both proposals A and B preferred Sunita as student union president

= 50/ (50 +50)%

= 50%

Hence, the fourth option is correct.

Q-3) What percentage of the students surveyed who did not support proposal A preferred Ragini as student union president?

1) 84

2) 83

3) 82

4) 85

Solution

We can represent the preferences of students who like Sunita and Ragini as disjoint sets in a Venn diagram:

Given: There are a total of 500 students in the survey.

From statement (2),

the number of students who prefer Sunita (S) is 200. Hence, the number of students who prefer Ragini (R) is 500 - 200 = 300.

From statement (1),

A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.

From statement (2),

the number of students who prefer Sunita and support Proposal A (A(S)) is 80% of 200, which is 160.

=> A (Sunita) = 160.

=> A (Ragini) = 90.

From statement (4),

20% of the total 250 students who support Proposal B prefer Sunita

=> B (Sunita) = 20 % of 250 = 50.

=> B (Ragini) = 200.

From statement (6),

=> g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110.

=> n (Sunita) = 40.

From statement (7),

=> n (Ragini) = 60

Now, it is given that 250 students support the proposal B

=> hence the other 250 students do not support proposal B.

From statement (5),

(a + n) of Ragini

= 40 % of 250

= 100.

Hence, a (Ragini) = 40.

Based on the above findings, the below Venn Diagram can be prepared:

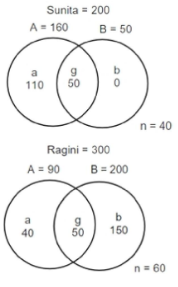
According to the Venn diagram,

The % of the students surveyed who did not support proposal A preferred Ragini as student union president

= 210/250

= 84%

Hence, the first option is correct.

Q-4) Among the students surveyed who supported proposal A, what percentage preferred Sunita for student union president?

1) 64

2) 63

3) 62

4) 61

Solution

We can represent the preferences of students who like Sunita and Ragini as disjoint sets in a Venn diagram:

Given: There are a total of 500 students in the survey.

From statement (2),

the number of students who prefer Sunita (S) is 200. Hence, the number of students who prefer Ragini (R) is 500 - 200 = 300.

From statement (1),

A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.

From statement (2),

the number of students who prefer Sunita and support Proposal A (A(S)) is 80% of 200, which is 160.

=> A (Sunita) = 160.

=> A (Ragini) = 90.

From statement (4),

20% of the total 250 students who support Proposal B prefer Sunita

=> B (Sunita) = 20 % of 250 = 50.

=> B (Ragini) = 200.

From statement (6),

=> g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110.

=> n (Sunita) = 40.

From statement (7),

=> n (Ragini) = 60

Now, it is given that 250 students support the proposal B

=> hence the other 250 students do not support proposal B.

From statement (5),

(a + n) of Ragini

= 40 % of 250

= 100.

Hence, a (Ragini) = 40.

Based on the above findings, the below Venn Diagram can be prepared:

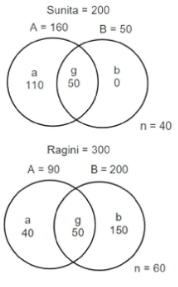
According to the Venn diagram,

Among the students who supported proposal A, the number of students who preferred Sunita

= 160

Therefore the % of these students is:

= 160 / (160 + 90)

= 160 / 250

= 64%
Hence, the first option is correct.

Binary Logic Reasoning Questions for CAT/ XAT/ MAT

Q-1) Directions: In an institute, there are three top rankers in a batch, Karthik, Waheeda, and Ritesh, not necessarily in the same order, who made the following statements about their ranks.

Karthik: (A) I am not the top ranker.

(B) Waheeda is not the second ranker.

(C) Ritesh is the third ranker.

Waheeda: (A) Karthik’s first statement is false.

(B) I am the third ranker.

(C) I made two false statements.

Ritesh: (A) Karthik is the first ranker.

(B) Waheeda is not the second ranker.

(C) I am the second ranker.

It is known that each of Karthik and Ritesh made only one false statement. Waheeda made only one true statement.

Q -1) : Which statement of Karthik and Ritesh is True?

1) 1

2) 2

3) 3

4) None

Solution

It is given that Waheeda made only one true statement. It implies that she made two false statements.

⇒ Waheeda’s third statement is true and the other two are false.

⇒ Karthik’s first statement is true. (From Waheeda’s first statement) i.e. Karthik is not the top ranker.

⇒ Ritesh’s first statement is false and the other two are true.

⇒ Ritesh is the second ranker and Waheeda is not the second ranker. As Karthik is not the first ranker, Waheeda is the first ranker and Karthik is the third ranker.

⇒ Karthik’s second statement is true and the third one is false.

Therefore, statement 2 is true of Karthik and Ritesh. Hence, the second option is correct.

Q-2) Directions: In an institute, there are three top rankers in a batch, Karthik, Waheeda, and Ritesh, not necessarily in the same order, who made the following statements about their ranks.

Karthik: (A) I am not the top ranker.

(B) Waheeda is not the second ranker.

(C) Ritesh is the third ranker.

Waheeda: (A) Karthik’s first statement is false.

(B) I am the third ranker.

(C) I made two false statements.

Ritesh: (A) Karthik is the first ranker.

(B) Waheeda is not the second ranker.

(C) I am the second ranker.

It is known that each of Karthik and Ritesh made only one false statement. Waheeda made only one true statement.

Q-2) If Waheeda’s statements are not considered, which of the following represents the correct order of truth and false statements made by Ritesh so that the rank of all three will not alter?

1) True, False, True

2) True, True, False

3) False, True, True

4) Cannot be determined

Solution

It is given that Waheeda made only one true statement. It implies that She made two false statements.

⇒ Waheeda’s third statement is true and the other two are false.

⇒ Karthik’s first statement is true. (From Waheeda’s first statement) i.e. Karthik is not the top ranker.

⇒ Ritesh’s first statement is false and the other two are true.

⇒ Ritesh is the second ranker and Waheeda is not the second ranker. As Karthik is not the first ranker, Waheeda is the first ranker and Karthik is the third ranker.

⇒ Karthik’s second statement is true and the third one is false.

Therefore, the arrangement is as follows:

Waheeda > Ritesh > Karthik

If Waheeda’s statements are not considered, then the correct order of truth and false statements made by Ritesh are False, true, and true. Hence, the third option is correct.

Q-3) Directions: In an institute, there are three top rankers in a batch, Karthik, Waheeda, and Ritesh, not necessarily in the same order, who made the following statements about their ranks.

Karthik: (A) I am not the top ranker.

(B) Waheeda is not the second ranker.

(C) Ritesh is the third ranker.

Waheeda: (A) Karthik’s first statement is false.

(B) I am the third ranker.

(C) I made two false statements.

Ritesh: (A) Karthik is the first ranker.

(B) Waheeda is not the second ranker.

(C) I am the second ranker.

It is known that each of Karthik and Ritesh made only one false statement. Waheeda made only one true statement.

Q-3) Who is the third ranker?

1) Karthik

2) Waheeda

3) Ritesh

4) Cannot be determined

Solution

It is given that Waheeda made only one true statement. It implies that She made two false statements.

⇒ Waheeda’s third statement is true and the other two are false.

⇒ Karthik’s first statement is true. (From Waheeda’s first statement) i.e. Karthik is not the top ranker.

⇒ Ritesh’s first statement is false and the other two are true.

⇒ Ritesh is the second ranker and Waheeda is not the second ranker. As Karthik is not the first ranker, Waheeda is the first ranker and Karthik is the third ranker.

⇒ Karthik’s second statement is true and the third one is false.

Therefore, the arrangement is as follows:

Waheeda > Ritesh > Karthik

Therefore, Karthik is the third ranker. Hence, the first option is correct.

For non verbal reasoning must read the below topics:

About the Faculty
Tanu Gupta, with over a decade of experience as a reasoning faculty, specializes in preparing students for various entrance examinations and career development. Her extensive work with multiple educational platforms and institutions has honed her expertise in logical and analytical thinking. Her dedication to innovative teaching methods ensures these articles provide practical insights and expert guidance.