Games and Tournaments: Meaning, Questions, Formula, Examples

Games and Tournaments are very commonly asked in CAT exams. To solve these questions you have to well-versed in this topic and types of games. Mostly, one to two sets are asked in the exam each set consists of 4-5 questions. These questions are asked to check your logical skills as logical reasoning skills are necessary for an aspirant because these skills help you think and reflect through outstanding decisions, create solutions and set goals. In this article you are able to learn games and tournaments formula, games and tournaments concepts, difference between cash games and tournaments etc.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: IBSAT 2024 Mock Tests | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

Question with Solutions: Missing Number | Alphabet Test | Arithmatical Problems | Calendar

This Story also Contains

1. Types of question asked in games and tournaments
2. Round Robin Tournament
3. Knockout Tournaments
4. Practice Questions on Games and Tournaments
5. Games and Tournaments Previous Year Cat Questions

Types of question asked in games and tournaments

The two types of questions are asked in the exam which are as follows:

(1) Round Robin Tournament

(2) Knockout Tournaments

Let’s discuss the types and games and tournaments CAT questions in detail:

Round Robin Tournament

It is defined as if the number of participants in a tournament is 8, then the round-robin tournament says every player will play with every other player exactly once.
Example:
Q1. The tournament has 8 teams: M, N, O, P, Q, R, S, T. Now find out how many matches the team plays in a tournament.
Solution:
According to round robin tournament each team will play with another team exactly once.
Therefore, M plays with N, O, P, Q, R, S, T which means M plays 7 matches. Similarly, N, O, P, Q, R, S, and T also play 7 matches each.
But it doesn’t mean that the total number of matches played by the teams in a tournament is 7 x 8 = 56.

Total number of matches played by the team M = M with N, M with O, M with P, M with Q, M with R, M with S, M with T = 7 matches.
The total number of matches played by the team N = (Match of N with M has already been counted above) Now other matches are N with O, N with P, N with Q, N with R, N with S, and N with T = 6 matches.
The total number of matches played by the team O = (Matches of O with M and N are already counted above) Now other matches are O with P, O with Q, O with R, O with S, O with T = 5 matches.
The total number of matches played by the team P = (Matches of P with M, N, O are already counted above) Now other matches are P with Q, P with R, P with S, and P with T = 4 matches
The total number of matches played by the team Q = (Matches of Q with M, N, O, P are already counted above) Now other matches are Q with R, Q with S, and Q with T = 3 matches.
The total number of matches played by the team R = (Matches of R with M, N, O, P, Q are already counted above) Now other matches are R with S, and R with T = 2 matches.
The total number of matches played by the team S = (Matches of S with M, N, O, P, Q, R are already counted above) Now other match of S is with T = 1 match.
The total number of matches played by the team T = (Matches of T with M, N, O, P, Q, R, S are already counted above)
Therefore, the total number of matches in the tournament = 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28
So, the total number of matches played by the teams in the tournament is equal to 28.

Now let's understand the games and tournaments CAT concepts:
How to calculate the total number of matches in the round-robin tournament using formulae?
We will consider the above example as there are a total of 8 teams.
The first team will be playing with the other 7 teams means the first team will play 7 matches, and the second team will also play the 7 matches but one match is already counted in the first case which means 6 matches are yet to be counted, Similarly, in the third, fourth, fifth, sixth, seventh and eighth the number of 5, 4, 3, 2, 1, 0 are yet to be counted.
Now you can calculate the total number of matches by using the formula of the sum of natural numbers which is as follows:
Sum of natural numbers = n(n + 1)/ 2
= 7(7 + 1)/2 = 7 x 8/ 2 = 28
So, the total number of matches = 28

Points to Remember in the Round Robin Tournament

1) There is a direct formula also to find out the total number of matches for a single round robin is NC2, where N is the total number of teams participating in the tournament.
2) If there are no draws, the number of wins is equal to the number of matches. It applies to a number of losses as well.
3) In case there are draws, the total number of wins + (total draws / 2) = the total number of matches.

Knockout Tournaments

It is defined as a tournament where one particular team or player will go out of the tournament the moment he loses a match. In this tournament, one team will be playing against another team the loser team will eliminated from the game and the winning team will proceed further.
There are some rules to solve the knockout tournament questions which are as follows:
1) Total number of matches = Total number of players - 1
2) If the total number of players is 2n where n is a natural number, then the total number of rounds is n.
(nth will be the final round).
3) The first-seeded player (rank 1) will play with the last-seeded player, rank 2 with the second-last-seeded player and so on.
4) The sum of the seed numbers of players playing in any round with n players will be equal to n + 1.
Note: A seed number means a particular rank. For example: 1st seeded player means a player who is on the first rank.
Example:
Directions: In a football tournament total number of players is 64. All players have been given a seed number starting from 1 to 64.
Q-1) How many matches will happen in the whole tournament?
1) 63
2) 64
3) 65
4) 66
Solution:
The number of matches in the tournament = The number of players in the tournament - 1
= 64 - 1
= 63
Hence, the first option is correct.

Q-2) How many rounds will it take to complete the tournament?
1) 2
2) 4
3) 6
4) 8
Solution:
The number of players needs to be represented in the form of 2 power n and n is the number of rounds that will take place.
Therefore, 64 = 26
The value of n is 6. So, the number of rounds will be 6.
Hence, the third option is correct.

Q-3) What will be the number of players playing in 3rd round?
1) 30
2) 32
3) 28
4) 16
Solution:
In round one, there are 64 players.
In round two there are 32 players (who win the first round).
So, in round third, there are 16 players (those who win the second round).
Hence, the fourth option is correct.

Q-4) What will be the seed number of the player playing against the 13th-seeded player in the 3rd round in case of no upsets?
1) 2
2) 4
3) 5
4) 6
Solution:
In round one 64 players will be playing.
In round two 32 players will be playing.
In round three16 players will be playing.
To find out the seed number you have to follow the rule that the sum of the seed numbers of players playing in any round with n players will be equal to n + 1.
So, here in round three, there are 16 players which means n + 1 = 16 + 1 = 17.
Therefore, in this case, the seed number of the player playing against 13th is 4 as 13 + 4 = 17
Hence, the second option is correct.

Q-5) What will be the seed number of the player playing against the 7th seeded player in the 2nd round in case of no upset?
1) 27
2) 26
3) 28
4) 29
Solution:
In round one 64 players will be playing.
In round two 32 players will be playing.
To find out the seed number you have to follow the rule that the sum of the seed numbers of players playing in any round with n players will be equal to n + 1.
So, here in round two, there are 32 players which means n + 1 = 32 + 1 = 33.
Therefore, in this case, the seed number of the player playing against 7th is 26 as 7 + 26 = 33
Hence, the second option is correct.

Practice Questions on Games and Tournaments

Directions: Q(1 - 5) Sixteen teams have been invited to participate in the ABC Gold Cup cricket tournament. The tournament is conducted in two stages. In the first stage, the teams are divided into two groups. Each group consists of eight teams, with each team playing every other team in its group exactly once. At the end of the first stage, the top four teams from each group advance to the second stage while the rest are eliminated. The second stage comprises several rounds. A round involves one match for each team. The winner of a match in a round advances to the next round, while the loser is eliminated. The team that remains undefeated in the second stage is declared the winner and claims the Gold Cup. The tournament rules are such that each match results in a winner and a loser with no possibility of a tie. In the first stage, a team earns one point for each win and no points for a loss. At the end of the first stage teams in each group are ranked based on total points to determine the qualifiers advancing to the next stage. Ties are resolved by a series of complex tie-breaking rules so that exactly four teams from each group advance to the next stage.
Q-1) What is the total number of matches played in the tournament?
(1) 28
(2) 55
(3) 63
(4) 35
Solution:
There shall be 8 teams in each group. Each team in a group shall be playing with every other team. Therefore, the total number of matches = n (n + 1)/ 2
= (7 × 8) / 2 = 28 in one group. So, in both groups, there shall be 56 matches. This is for the first stage.
At the second stage, 4 matches (Round 1) + 2 matches (Round 2) + 1 Match (Round 3) = 7
So, the total number of matches is 56 + 7 = 63. Hence, the third option is correct.

Q-2) The minimum number of wins needed for a team in the first stage to guarantee its advancement to the next stage is:
(1) 5
(2) 6
(3) 7
(4) 4
Solution:
A team can be terminated even if it wins 5 of its 7 matches (as 5 teams can win 5 matches each that is 5 + 5 + 5 + 5 + 5 + 2 + 1 + 0). The logic behind this is that in each group there are 8C2 = 28 matches.
So, the winners are 28.
Thus, 5 teams can't win 6 matches each. Therefore, if a team wins six matches it is safe. However, if a team wins 5 matches, 4 more teams could also have won 5 matches each and in that case, the team would get terminated. Thus, advancement is not guaranteed with 5 wins. So, 5 + 1 wins are needed for the advancement. Hence, the second option is correct.

Q-3) How many rounds are in the second stage of the tournament?
(1) 1
(2) 2
(3) 3
(4) 4
Solution:
There are three rounds in the second stage of the tournament which is as follows:
(1) Quarterfinals
(2) Semifinals
(3) Finals
Hence, the third option is correct.

Q-4) What is the highest number of wins for a team in the first stage despite which it would be eliminated at the end of the first stage?
1) 5
2) 3
3) 2
4) 1
Solution:
In the first round, there are 28 matches of 8 player groups in a total of 28 wins.
To determine this, we need the top 5 teams to win nearly equal matches.
Suppose each of the top 5 teams wins 5 matches each and the remaining 3 matches are won by the bottom 2 teams. The qualifiers will be decided based on the tie-breaking rules. Therefore, even with 5 wins a team may end up not qualifying for the next round. Hence, the first option is correct.

Q-5) Which of the following statements is true?

1) The winner will have more wins than any other team in the tournament.
2) At the end of the first stage, no team eliminated from the tournament will have more wins than any of the teams qualifying for the second stage.
3) The number of teams with exactly one win in the second stage of the tournament is 4.
4) It is possible that the winner will have the same number of wins in the entire tournament as a team eliminated at the end of the first stage.
Solution:
To find out the true statement. Consider the following situations:

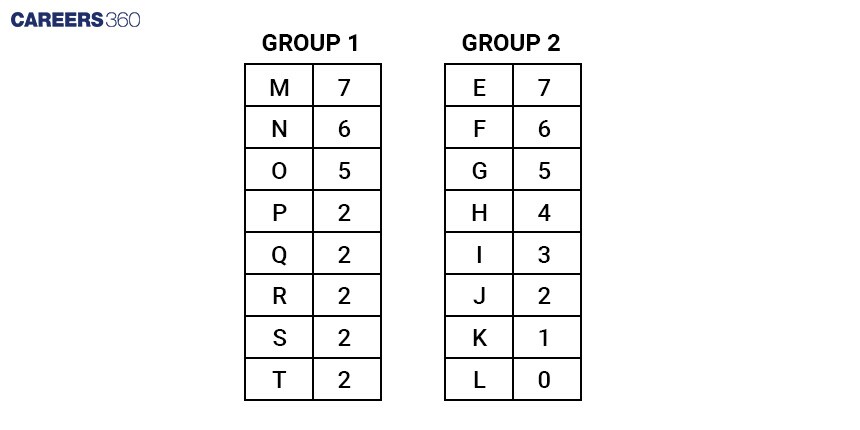
First Option: If P wins the tournament he will have 5 wins. But if E loses in the second round, he would have 7 wins. Therefore, the first option is incorrect.
Second Option: You can see that I have more wins than P. Therefore, the second option is incorrect.
Third Option: Consider the following situations:

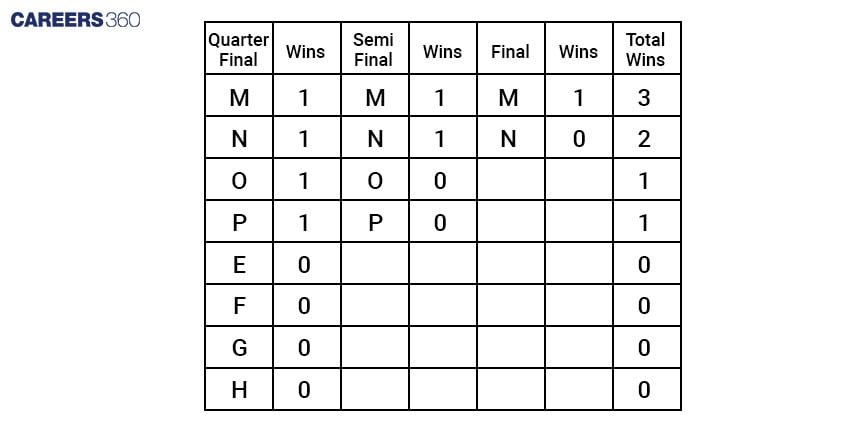
According to the above table, you can see that 2 teams have one win each in the second stage. Therefore, the third option is incorrect.
Fourth Option: Consider the following situations:

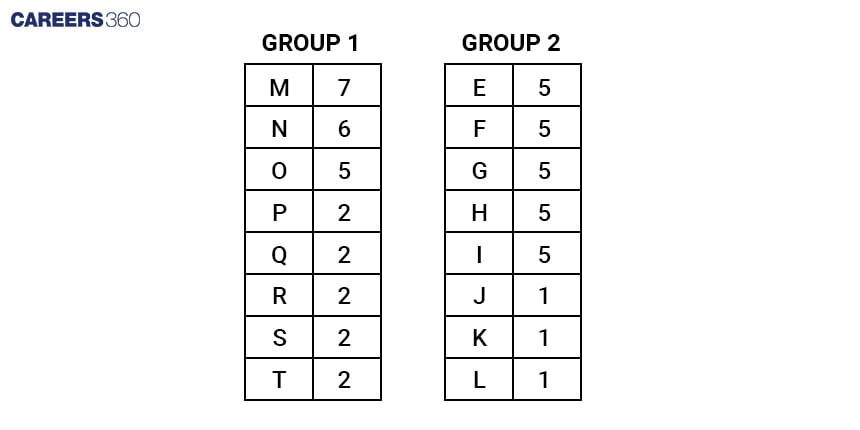
If P wins the tournament he would have 5 wins. But I would lose the tournament with 5 wins. Hence, the fourth option is correct.

Directions: Q(6-9) In the table below is the listing of players, seeded from highest (#1) to lowest (#32), who are due to play in an Association of Tennis Players (ATP) tournament for women. This tournament has four knockout rounds before the final, i.e., first round, second round quarterfinals and semi-finals. In the first round, the highest-seeded player plays the lowest-seeded player (seed#32), designated match No. 1 of the first round; the 2nd-seeded player plays the 31st-seeded player, designated match No. 2 of the first round, and so on. Thus, for instance, match No. 16 to the first round will be played between the 16th-seeded player and the 17th-seeded player. In the second round, the winner of match No.1 of the first round plays the winner of match No. 16 of the first round and is designated match No.1 of the second round.

Similarly, the winner of match No.2 of the first round lays the winner of match No.15 of the first round and is designated match No. 2 of the second round. Thus, for instance, match No. 8 of the second round will be played between the winner of match No. 8 of the first round and the winner of match No. 9 of the first round. The same pattern is followed for later rounds as well.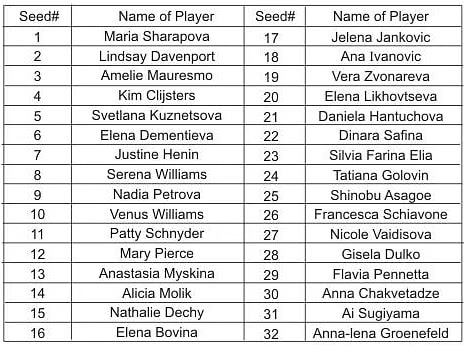

Q-6) If there are no upsets (a lower-seeded player beating a higher-seeded player) in the first round, and only match Nos. 6, 7, and 8 of the second round result in upsets, then who would meet Lindsay Davenport in quarter-finals, in case Davenport reaches quarter-finals?
1) Justine Henin
2) Nadia Petrova
3) Patty Schnyder
4) Venus Williams
Solution:
There are no upsets in the first round. Thus, the top 16 players go to the 2nd round.
In the second round, the nth player would play (17 - n)th player. Now, matches no. 6, 7, and 8 of the second round result are upsets.
Therefore, the people in the quarter-finals would be 1, 2, 3, 4, 5, 11, 10, 9.
So, in the quarterfinal, 2nd seeded player would play (9 - 2) = 7th position player.
Here, no. 10 is in the 7th position and the No.10 player is Venus Williams.
Hence, the fourth option is correct.

Q-7) If Elena Dementieva and Serena Williams lose in the second round, while Justine Henin and Nadia Petrova make it to the semi-finals, then who would play Maria Sharapova in the quarterfinals, in the event Sharapova reaches the quarterfinals?
1) Dinara Safina
2) Justine Henin
3) Nadia Petrova
4) Patty Schnyder
Solution:
If Elena Dementieva and Serena Williams lose in the second round, Nadia Petrova and Patty Schnyder will go through.
Therefore, following seed no. players will be in the quarter-final.
1,2,3,4,5,11,7,9.
Therefore, now Maria Sharapova is ranked 1 so she'll play 9th seed player, Nadia Petrova. Hence, the third option is correct.

Q-8) If, in the first round, all even-numbered matches (and none of the odd-numbered ones) result in upsets, and there are no upsets in the second round, then who could be the lowest-seeded player facing Maria Sharapova in the semi-finals?
1) Anastasia Myskina
2) Flavia Pennetta
3) Nadia Petrova
4) Svetlana Kuznetsova
Solution:
According to a given condition, players of the following ranking will go to the 2nd round 1, 31, 3, 29, 5, 27, 7, 25, 9, 23, 11, 21, 13, 19, 15, 17.
Out of these players going to the 3rd round/quarter-finals are 1,15, 3, 13, 5, 11, 7, 9.
If Maria (no.1) goes to the semifinal she'll face anyone out of the 13/5 th no. player in semis.
The 13th seed player is the lowest thus, Anastasia Myskina.
Hence, the first option is correct.

Q-9) If the top eight seeds make it to the quarterfinals, then who, amongst the players listed below, would definitely not play against Maria Sharapova in the final, in case Sharapova reaches the final?
1) Amelie Mauresmo
2) Elena Dementieva
3) Kim Clijsters
4) Lindsay Davenport
Solution:
If the top eight seeds make it to the quarterfinals then one out of Kim Clijsters or Svetana Kuznetsova will compete with Maria Sharapova in the semis.
Now if Maria reaches the semis, she'll beat anyone out of the two and both will not play against Maria Sharapova in the final if she reaches.
Hence, the third option is correct.

Note: The candidate must read the games and tournaments concepts pdf and should practice the games and tournaments questions pdf available online.

Games and Tournaments Previous Year Cat Questions

Directions: Q (1-5) In a school quiz competition, there are 10 teams, and each team competes against each of the other teams exactly once. In this scoring system, each win is worth 3 points, a draw is worth 1 point, and a loss is worth (–1) points. The final standings are as follows:

Team Phoenix – 27 points

Team Tiger – 18 points

Team Falcon – 14 points

Team Lion – 10 points

Team Dolphin – 8 points

Team Wolf – (–9) points

Team Eagle – 5 points

Team Bear – 4 points

Team Panda – 2 points

Team Giraffe – 0 points

Q-1) Find the team that had scored approximately the average of all the points scored by the teams.

1) Team Phoenix

2) Team Lion

3) Team Dolphin

4) Team Eagle

Solution

The total points scored by all teams is:

27 (Phoenix) + 18 (Tiger) + 14 (Falcon) + 10 (Lion) + 8 (Dolphin) – 9 (Wolf) + 5 (Eagle) + 4 (Bear) + 2 (Panda) + 0 (Giraffe) = 79

The average points would be the total points divided by the number of teams (10):

Average points = 79 ÷ 10 = 7.9

So, the average points scored by all teams is 7.9.

Team Dolphin with 8 points is the closest to the average of 7.9.

Therefore, Team Dolphin scored approximately the average of all the points scored by the teams.

Hence, the third option is correct.

Q-2) Find the number of games drawn by Team Eagle if they had won 3 games and lost 5 games.

1) 2

2) 3

3) 4

4) 1

Solution

If Team Eagle won 3 games and lost 5 games, we can find the number of games drawn by subtracting these wins and losses from the total number of matches they played.

In the round-robin format, each team plays against every other team exactly once. Since there are 10 teams, each team plays 9 matches.

So, Team Eagle played a total of 9 matches, and they won 3 games and lost 5 games. To find the number of games drawn:

Number of games drawn = Total matches – Wins + Losses

Number of games drawn = 9 – (3 + 5)

Number of games drawn = 9 – 8

Number of games drawn = 1

Team Eagle drew 1 game.

Hence, the fourth option is correct.

Q-3) Find the finalists.

1) Team Phoenix and Team Tiger

2) Team Phoenix and Team Bear

3) Team Falcon and Team Lion

4) Team Tiger and Team Dolphin

Solution

To find the finalists in the quiz competition, we typically look for the teams with the highest scores. In this case, Team Phoenix had the highest score with 27 points.

Now, let's determine the second finalist. Team Tiger had the second-highest score with 18 points.

So, the finalists are:

1. Team Phoenix

2. Team Tiger

Hence, the first option is correct.

Q-4) Which team lost all the matches?

1) Team Wolf

2) Team falcon

3) Team Panda

4) Team Dolphin

Solution

Team Wolf lost all their matches. They finished with a score of –9, indicating that they lost all their 9 games.

Hence, the first option is correct.

Q-5) How many matches did Team Phoenix play?

1) Team Phoenix played 7 matches

2) Team Phoenix played 9 matches

3) Team Phoenix played 10 matches

4) Team Phoenix played 12 matches

Solution

Team Phoenix played 9 matches in the tournament. In a tournament with 10 teams where each team plays against every other team exactly once, each team plays (10 – 1) = 9 matches.

Hence, the second option is correct.

Directions: Q (6-10) In a basketball tournament, eight teams are participating. Each team plays against every other team exactly once. If a team receives 2 points for a win, 1 point for a draw, and 0 points for a loss, the final standings are as follows:

Team X – 15 points

Team Y – 12 points

Team Z – 11 points

Team W – 10 points

Team V – 9 points

Team U – 8 points

Team T – 7 points

Team S – 6 points

Q-6) List the teams that scored below the average point.

1) Team X, Team Y, Team Z

2) Team W, Team V, Team U

3) Team Y, Team Z, Team S

4) Team S, Team T, Team U

Solution

The average points can be calculated as the total points earned by all teams divided by the number of teams. In this case, there are 8 teams in the tournament.

Total points earned by all teams = 15 (X) + 12 (Y) + 11 (Z) + 10 (W) + 9 (V) + 8 (U) + 7 (T) + 6 (S) = 78 points

Average points = Total points ÷ Number of teams

Average points = 78 ÷ 8 = 9.75 points

Now, we can list the teams that scored below the average points (less than 9.75 points):

1. Team S – 6 points

2. Team T – 7 points

3. Team U – 8 points

Hence, the fourth option is correct.

Q-7) Which 4 teams qualify for the playoffs?

1) Team X, Team Z, Team V, Team S

2) Team Y, Team W, Team U, Team T

3) Team X, Team Y, Team Z, Team W

4) Team V, Team U, Team T, Team S

Solution

To determine which four teams qualify for the playoffs, we can identify the top four teams with the highest points in the given standings.

The top four teams with the highest points are:

1. Team X - 15 points

2. Team Y - 12 points

3. Team Z - 11 points

4. Team W - 10 points

These are the top four teams in terms of points, and they qualify for the playoffs.

Hence, the third option is correct.

Q-8) How many games did T lose if they had won 3 games and drew one?

1) 1

2) 2

3) 3

4) 4

Solution

Number of games lost = Total games played – (Games won + Games drawn)

Number of games lost = 7 – (3 + 1)

Number of games lost = 7 – 4

Number of games lost = 3

So, Team T lost 3 games in the tournament.

Hence, the third option is correct.

Q-9) How many games did X win if they had not lost a single game and none of their matches went down as a draw?

1) 5

2) 6

3) 7

4) 8

Solution

If Team X has not lost a single game and one of their matches ended in a draw, we can deduce the number of games they won.

Team X has 15 points in total. In this tournament, a win is worth 2 points, a draw is worth 1 point, and a loss is worth 0 points. Since Team X has 15 points, this means that they must have won several games and had one draw.

2W = 14

W = 7

So, Team X won 7 games in the tournament.

Hence, the third option is correct.

Q-10) In the given basketball tournament standings, which team is in the fifth position from the bottom based on their points?

1) Team Z

2) Team V

3) Team T

4) Team W

Solution

Let's arrange the teams in ascending order based on their points and confirm that Team W is indeed the fifth team from the bottom:

Team X – 15 points

Team Y – 12 points

Team Z – 11 points

Team W – 10 points

Team V – 9 points

Team U – 8 points

Team T – 7 points

Team S – 6 points

Team W has 10 points, which makes it the fifth team from the bottom.

Hence, the fourth option is correct.

The candidates who are preparing for the upcoming CAT exam can also refer to the links given below and master the reasoning ability section:

About the Faculty
Tanu Gupta, with over a decade of experience as a reasoning faculty, specializes in preparing students for various entrance examinations and career development. Her extensive work with multiple educational platforms and institutions has honed her expertise in logical and analytical thinking. Her dedication to innovative teaching methods ensures these articles provide practical insights and expert guidance.