Fundamentals of Geometry for 3D Shapes: Concepts and Principles
Aspiring students and designers must have a solid understanding of area and volume. Knowledge of the volumes is critical in form analysis, spatial perception, and problem-solving skills. This essential skill aids the ability to visualize and deal with 3D objects, making it relevant to the DAT ability test. The students who understand these concepts will provide a good foundation for making good fortunes in the design field. As for the perceptual value of the given 3D forms, it is helpful to solve critical questions from the NAT section for exams like NID and UCEED, which contains relatively easy questions to score.
3D Shapes Geometry and Their Properties:
This Story also Contains
- 1. Cube & Cuboid:
- 2. Sphere and Hemisphere
- 3. Cylinder
- 4. Cone
- 5. Pyramid
- Sample Questions:

Below is a breakdown of 3D shapes properties with specific examples. Understanding these Geometry of three-dimensional shapes enhances problem-solving abilities and spatial visualization in design tasks.
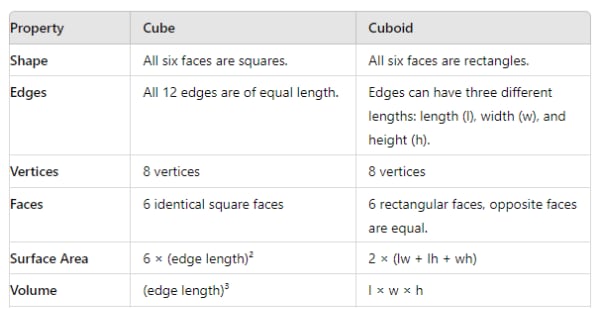
1. Cube & Cuboid:
Three-dimensional shapes that come under the class of polyhedral are stable solid bodies with flat faces. There are two crucial shapes known as the cube and the cuboid. These two shapes are identical in that they possess twelve edges, six faces and eight vertices; nevertheless, they are entirely dissimilar in size and shape.
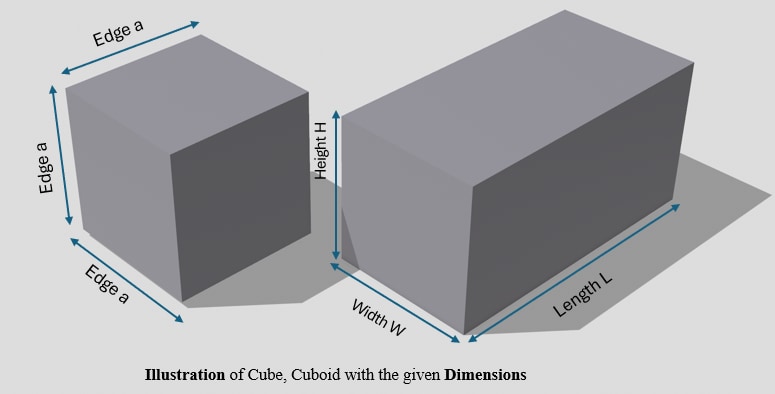
Comparison of Cube and Cuboid
Note: All sides of the cube are equal, and the length taken is “a” units.
Similarly, for the cuboid, Length (l units), Breadth (b units) and Height (h units)
Knowing the fundamentals of 3D Geometry makes it simple to differentiate between the cube and cuboid characteristics and use them for creative endeavors.
2. Sphere and Hemisphere
Rounded solids include both hemispheres and spheres, which are three-dimensional shapes. They possess unique mathematical qualities and are frequently encountered in organic forms.
Sphere
A sphere is a three-dimensional object that is precisely spherical and has equal distances between each point on its surface and the center. It has no edges or vertices and is the three-dimensional equivalent of a circle.

Note: All points on the surface are equidistant from the center in a sphere.
Hemisphere
When a given sphere is cut along its diameter to reveal a hemisphere, which is precisely half of a sphere, its surface is curved, and its base is a flat circular face. Unlike a sphere, it has a boundary running along its circular base but no edges or vertices on its curved surface.

For a Hemi-Sphere
Note: A hemisphere with a flat surface is made by cutting a sphere from the center.

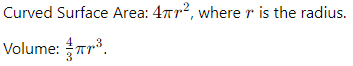
You may also check:
These are some of the topics that are generally also asked in DAT exams. Students can go through for their design entrance exam preparations.
3. Cylinder
A three-dimensional geometric object called a cylinder comprises two parallel circular bases joined by a curved surface. One of the most prevalent 3D shapes properties can be found in many natural and artificial artefacts. The height in a cylinder is the vertical distance between two faces of the cylinder.

4. Cone
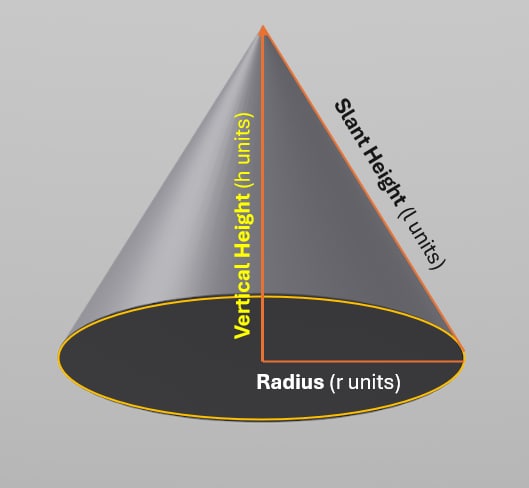
A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the center of the base) called the apex or vertex. Cones are frequently visible in man-made and natural forms, such as volcanic mountains, ice cream cones etc.
For a cone with a height (h units), slant height (l) and base radius (r units)

5. Pyramid
A pyramid is a three-dimensional geometric form consisting of triangular faces that converge at a single point known as the apex or vertex and a polygonal base. The name of a pyramid is determined by the type of base, like a triangular, square or a based pyramid.
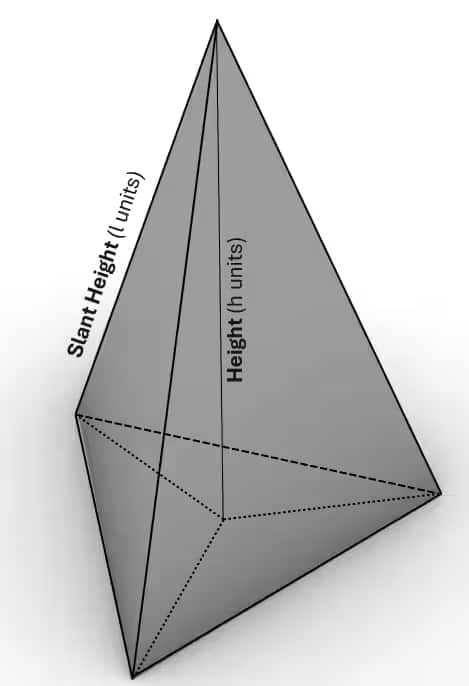
In a pyramid with a triangular base, for the given height (h), slant height (l) and having a triangular base, the area can be calculated as follows:
Pyramid: With a Triangular Base(3 sided base)

Sample Questions:
Q1:
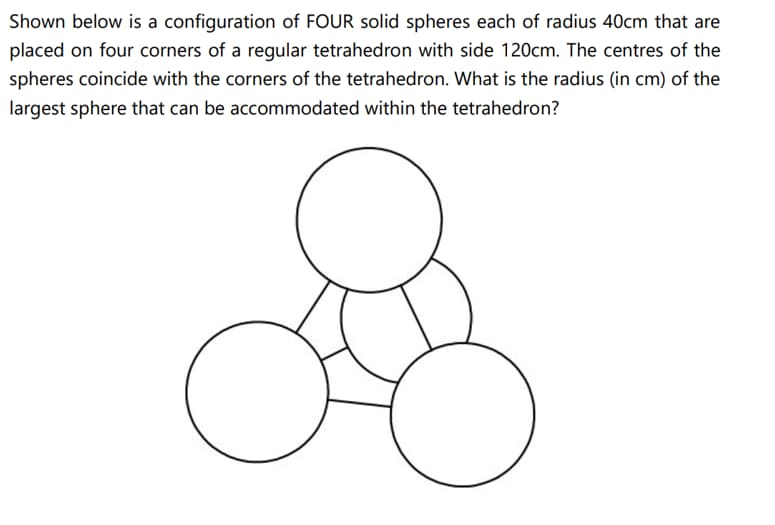
Solution: We can calculate the required radius using the relationship between the tetrahedron's edge and the inscribed sphere. Let's calculate the radius step by step.
Formula for Radius of the Sphere Inside the Tetrahedron:
The radius r of the largest sphere that can fit inside the tetrahedron can be calculated using the formula:
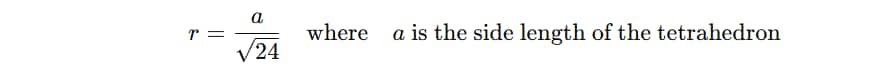
Given that the side length a=120cm, we can substitute this value into the formula.
Therefore, The radius of the largest sphere that can be accommodated within the tetrahedron is approximately 24.5 cm.
Q2: A tetrahedron of side 18 units and a cone having a base diameter of 10 units are cutting through a sphere as shown. Count the total number of surfaces in the resultant sphere.
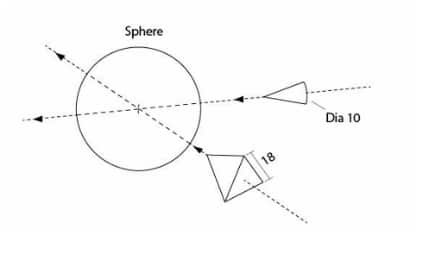
Solution:
- Tetrahedron: A regular tetrahedron has 4 triangular faces.
- Cone: A cone cutting through the sphere has a circular base. The number of surfaces in a cone is typically two: the curved surface and the base.
- Sphere: The sphere itself has one surface, but since it is being cut by the cone and tetrahedron, new surfaces will form where these objects intersect the sphere.
Total Surfaces:
- Tetrahedron: The 4 triangular faces of the tetrahedron intersect the sphere, contributing new surfaces.
- Cone: The cone also creates an intersection surface on the sphere.
From these, the total number of surfaces in the resultant figure would be:
- 4 surfaces from the tetrahedron (the 4 triangular faces)
- 1 surface from the cone's base
- 1 curved surface from the cone
Thus, the total number of surfaces in the resultant sphere is 6.
Q3: The given 3D object is made by combining three shapes - pentagons, squares and triangles. What is the total number of squares?
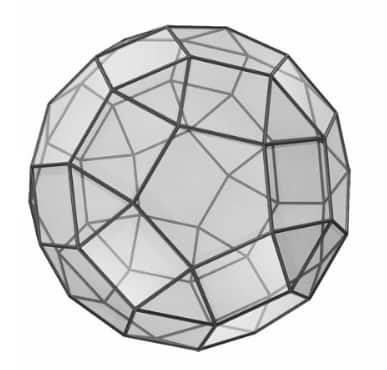
Solution:
The given 3D shape is a truncated icosidodecahedron, a well-known polyhedron composed of three types of faces:
- 30 squares
- 20 hexagons
- 12 decagons
Therefore, answer is 30 squares
You can count them visually too — they are the quadrilateral faces bordered by four edges, arranged symmetrically across the shape.
Frequently Asked Questions (FAQs)
By enhancing spatial thinking skills, form analysis and problem-solving skills all these are essential for being able to see as well as interact with three-dimensional objects in the design tasks, thus mastering 3o geometry is compulsory to pass the DAT exam.
A cuboid has dimensions in three different directions as opposed to a cube where the sides have the same measurement. In fact, although the sizes of both forms are different and their proportions different, too, their Plane Geometrical symmetry is the same, namely both are 12-edged, 8-vertex, and both include six faces.
Owing to the knowledge of the characteristics of spheres and hemispheres the accurate calculation of surface area and volume is made and it is useful in the goal of creating balanced functional forms in constructs and in nature.
There is the use of pyramids that are used in the different architectures, especially in the triangles. The geometry of these figures is important so as to compute the surface area and volume; and both are especially needed in the DAT examinations in design, structure and architecture assignments.
Cones are frequently visible in man-made and natural forms, such as volcanic mountains, ice cream cones etc.