Bragg's Law
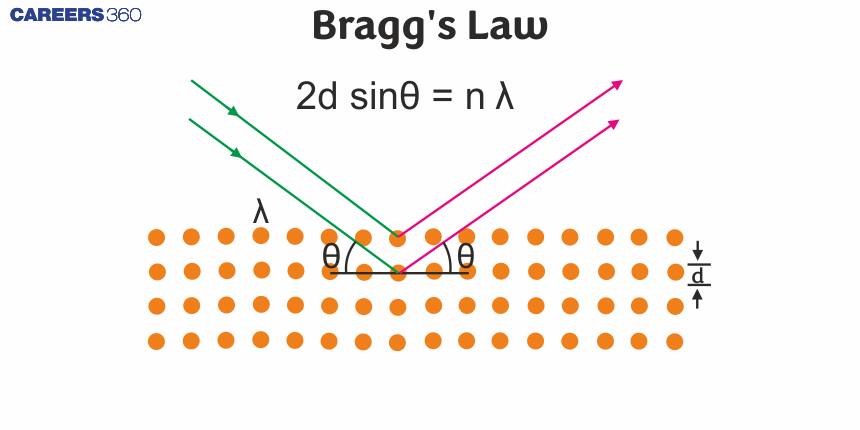
How do scientists determine the exact arrangement of atoms inside a crystal without ever seeing them? And why do certain angles of X-ray reflection produce sharp peaks, while others show nothing at all? You will get all these answers by studying Bragg's law. Bragg's is a fundamental principle describing the diffraction of X-rays by crystal lattices. This law defines how X-rays will set up constructive interference at particular angles, which form part of the atomic planes in crystals. Mathematically, this interaction is represented by the equation nλ=2dsinθ, whereθ is the angle of incidence and reflection.
This Story also Contains
- Superconductivity
- Cohesive Energy
- Bragg’s Equation
- Bragg’s Application
- Some Solved Examples
- Summary
Superconductivity
Kammerlingh Onnes observed this phenomenon at 4 K in mercury. A substance is said to be superconducting when it offers no resistance to the flow of electricity. There is no substance that is superconducting at room temperature. Superconductors are widely used in electronic power transmission, building supermagnets, etc. For example, YBa2Cu3O7, Nb3Ge alloy, (TMTSF)2PF6, etc.
Cohesive Energy
It is the energy needed to achieve infinitely separated gaseous ions from one mole of an ionic crystal lattice that is negative of the Lattice energy.
MX(s)→M+(g)+X(g)
Bragg’s Equation
This equation gives a simple relationship between the wavelength Of X-rays the distance between the planes in the crystal and the angle Of reflection. This equation can be written as:
$\begin{aligned} & \mathrm{n} \lambda=2 \mathrm{~d} \sin \theta \\ & \text { Here } \\ & \mathrm{n}=\text { Order of reflection; in general it is taken as } 1 . \\ & \lambda=\text { Wavelength of } \mathrm{X} \text { - rays } \\ & \mathrm{d}=\text { Distance between two layers of the crystals } \\ & \theta=\text { Angle of incident light }\end{aligned}$ As for a given set of lattice planes, the value of 'd' is fixed so the possibility of getting maximum reflection depends only on θ. If we increase θ gradually a number of positions will be observed at which there will be maximum reflection.

Bragg’s Application
- Bragg's observation has proved highly beneficial in determining the structures and dimensions of ionic crystalline solids.
- It also helped in describing many properties of X-rays.
- It helped in the construction of an X-ray spectrometer by which the crystalline structure of crystals can be easily described. For example, the face-centered cubic structure of NaCl.
Recommended topic video on(Bragg's Law)
Some Solved Examples
Example 1: In superconductivity, the electrical resistance of material becomes?
1) Zero
2)Infinite
3)Finite
4)All of the above
Solution
Superconductors are those materials that have zero electrical resistance or infinite conductance.
Their conductivity is known as superconductivity.
Hence, the answer is the option (1).
Example 2: Which of the following relation is correct for first order Bragg’s diffraction?
1)$\sin \Theta=\frac{2 a}{\lambda}\left(h^2+k^2+l^2\right)$
2)$\sin \Theta=\frac{2 a}{\lambda}\left(h^2+k^2+l^2\right)^{\frac{1}{2}}$
3) $\sin \Theta=\frac{\lambda}{2 a}\left(h^2+k^2+l^2\right)^{\frac{1}{2}}$
4)$\sin \Theta=\frac{\lambda}{2 a}\left(h^2+k^2+l^2\right)^2$
Solution
Bragg’s Equation
This equation gives a simple relationship between the wavelength Of X-rays the distance between the planes in the crystal and the angle Of reflection. This equation can be written as:
$
\mathrm{n} \lambda=2 \mathrm{~d} \sin \theta
$
Here $\mathrm{n}=$ Order of reflection; in general it is taken as 1.
$\lambda=$ Wavelength of $\mathrm{X}-$ rays
$\mathrm{d}=$ Distance between two layers of the crystals
$\theta=$ Angle of incident light
As for a given set of lattice planes the value of 'd' is fixed so the possibility of getting maximum reflection depends only on θ. If we increase θ gradually a number of positions will be observed at which there will be maximum reflection.
Now,
$n \lambda=2 d \sin \Theta$
Thus, $d=\frac{\lambda}{2 \sin \Theta} \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots(i)$
Again, we have
$d=\frac{a}{\sqrt{h^2+k^2+l^2}} \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots(i i)$
On combining both these equations, we have
$\frac{\lambda}{2 \sin \Theta}=\frac{a}{\sqrt{h^2+k^2+l^2}}$
Thus, $\sin \Theta=\frac{\lambda}{2 a}\left(h^2+k^2+l^2\right)^{\frac{1}{2}}$
Therefore, Option(3) is correct.
Example 3: Calculate the wavelength of X-rays, which produces a diffraction angle $2 \theta$ equal to $16.8^{0}$ for a crystal. Assume first order diffraction with inter particle distance in crystal of 0.2nm.
1)$58.4 \times 10^{-11} \mathrm{~m}$
2)$4.3 \times 10^{-11} \mathrm{~m}$
3)$3.7 \times 10^{-11} \mathrm{~m}$
4) $5.8 \times 10^{-11} \mathrm{~m}$
Solution
We have given,
n = 1, $d=0.2 \times 10^{-9} \mathrm{~m}$
Thus, $\theta=16.8 / 2=8.4^{\circ}$
Therefore $\lambda=\frac{2 \times 0.2 \times 10^{-9} \times \sin 8.4}{1}$
Thus, $\lambda=5.84 \times 10^{-11} \mathrm{~m}$
Therefore, Option(4) is correct
Example 4: Pure silicon is an insulator but on heating it becomes a semi-conductor because:
1)On heating, electrons occupy higher energy states
2)No effect on electrons on increasing temperature
3)On heating, electrons move freely in crystals
4) Both (1) and (3)
Solution
Pure silicon has its electrons in a lower energy state. An increase in temperature promotes the electrons to occupy higher energy states. These electrons move freely in crystals and are responsible for electrical conduction.
Hence, the answer is the option (4).
Example 5: In Bragg's equation for diffraction of X-rays, n represents:
1)Quantum number
2) An integer
3)Avogadro's number
4)moles
Solution
As we learned,
Bragg's Equation
$\mathrm{n} \lambda=2 \mathrm{~d} \sin \theta$
Here, n represents an integer that is multiplied by the wavelength and represents phase waves for the determination of the distance between the planes.
Hence, the answer is option (2).
Practice More Questions With The Link Given Below
Summary
Bragg's Law made immense contributions to scientific discovery—like the discovery of the DNA double helix structure—thus remaining one of the cornerstones of modern material science. We can think of X-rays as waves that not only interact with several layers of atoms inside a crystal but in such a way that all the reflected waves add up to produce very strong signals at specific angles