Law of mass action

The Norwegian Chemists Cato Guldberg and Peter Waage discovered the law of mass action in 1864. The law of mass action became very important in chemical kinetics and thermodynamics and later it influenced various theories and models such as rate laws in reaction kinetics and the principle of chemical thermodynamics

JEE Main 2025: Chemistry Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics |  PYQs

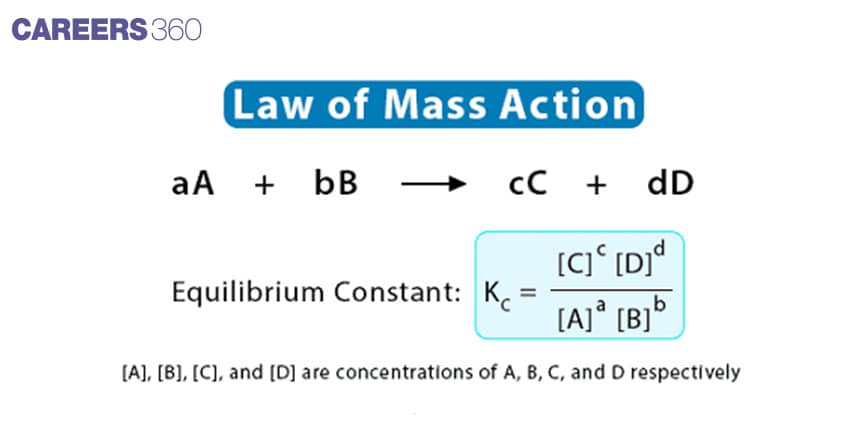
The law of mass action states that the reaction rate is proportional to the product of the concentration of the reactants. In this law, the rate of reaction is proportional to the product concentration, each raised to the power equal to the coefficient in the balanced chemical reaction or equation.

Law Of Mass Action

It was introduced by Guldberg and Waage. It states that “the rate at which a substance reacts is directly proportional to its activity and the rate at which substances react together is directly proportional to the product of their activity each raised to a power which is equal to the corresponding stoichiometric number the substance present in the chemical reaction".

mA+nB⇌pC+qD

Activity is generally Represented in terms of concentration or pressure of species involved

If active masses of A, B, C, and D are represented in terms of their concentrations [A], [B], [C], and [D] respectively, then:

Rate of reaction of A ∝ [A]^m

Rate of reaction of B ∝ [B]ⁿ

_R1 ∝ [A]^m [B]ⁿ = K₁ [A]^m[B]ⁿ

_R2 ∝ [C]^p [D]^q = K₂ [C]^p [D]^q

NOTE: For pure solids or pure liquids, activity is always unity (1).

Recommended topic video on (Law of mass action )

Some Solved Examples

Example 1. The equation that relates the values of amounts of product and reactant at equilibrium is called

1)law of conservation of mass

2)Active mass

3) (correct)Law of mass action

4)none of these

Solution

Law of Mass Action -“The rate at which a substance reacts is directly proportional to its active mass and the rate of a chemical reaction is directly proportional to the product of active masses of reactants each raised to a power equal to corresponding stoichiometric coefficient appearing in the balanced chemical equation”.

aA+bB⇌cC+dD

rate of reaction ∝ [A]^a.[B]^b

rate of reaction = K[A]^a[B]^b

where K is the rate constant or velocity constant of the reaction at that temperature.

Hence, the answer is the option (3).

Example 2. The rate at which the reaction proceeds is directly proportional to:

1)Product of the active masses of products

2) (correct)Product of the active masses of reactants

3)Both 1 and 2

4)None

Solution

According to the law of mass action, for a reversible single-step reaction, the rate of forward reaction (the rate at which the reaction proceeds) is directly proportional to the product of active masses of all the reactants.

Hence, the answer is the option (2).

Example 3. The term "active mass" shows the concentration of reactants and products in:

1) (correct) moldmm−3 for a dilute solution
2) molcm−3 for a dilute solution
3) molcm−3 for a concentrated solution.
4) moldm−3 for a concentrated solution.

Solution

The term "active mass" shows the concentration of reactants and products in moldm−3 because of concentration =nv=mol litre

Hence, the answer is the option (1).

Example 4. For equilibrium A⇌B, the variation of the rate of the forward (a) and reverse (b) reaction with the time is given by:

1)

2) (correct)

3)

4)

Solution

At equilibrium

Rate of forward = Rate of backward

So, a = b Hence

The correct graph will be -

Therefore, the correct option is (2).

5. The reaction rate for the reaction
$
\left[\mathrm{PtCl}_4\right]^{2-}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons\left[\mathrm{Pt}\left(\mathrm{H}_2 \mathrm{O}\right) \mathrm{Cl}_3\right]^{-}+\mathrm{Cl}^{-}
$
was measured as a function of concentrations of different species. It was observed that
$
\frac{-\mathrm{d}\left[\left[\mathrm{PtCl}_4\right]^{2-}\right]}{\mathrm{dt}}=4.8 \times 10^{-5}\left[\left[\mathrm{PtCl}_4\right]^{2-}\right]-2.4 \times 10^{-3}\left[\left[\mathrm{Pt}\left(\mathrm{H}_2 \mathrm{O}\right) \mathrm{Cl}_3\right]^{-}\right]\left[\mathrm{Cl}^{-}\right]
$
where square brackets are used to denote molar concentrations. The inverse of the equilibrium constant $\frac{1}{\mathrm{~K}_{\mathrm{c}}}=$ = __________.(Nearest integer)

1) (correct)50

2)20

3)30

4)40

Solution

As we have learned,

For any reversible reaction,
Rate $=\mathrm{K}_{\mathrm{f}}[$ Reactant $]-\mathrm{K}_{\mathrm{b}}$ [Product $]$
$\therefore$ Comparing with the given rate law expression
$
\begin{aligned}
& \mathrm{K}_{\mathrm{f}}=4.8 \times 10^{-5} \\
& \mathrm{~K}_{\mathrm{b}}=2.4 \times 10^{-3} \\
& \therefore \mathrm{K}_{\mathrm{c}}=\frac{\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{b}}}=\frac{4.8 \times 10^{-5}}{2.4 \times 10^{-3}}=0.02 \\
& \therefore \frac{1}{\mathrm{~K}_{\mathrm{c}}}=50
\end{aligned}
$

Hence, the answer is (50).

Summary

The law of mass action has various applications in chemical equilibrium and rate law. The rate law explains how the rate of reaction depends on the concentration of the reactant and which is used to predict the reaction rates of any particular reaction which is very useful in understanding the dynamics of a chemical process.