Packing Efficiency Of A Unit Cell

In solid-state chemistry, the unit cell is the smallest repeating structure of the crystal. Packing efficiency is the measure of how compactly atoms, ions, or molecules are arranged within a unit cell. It is, therefore, a way to understand just how much available space in the unit cell actually gets occupied by constituent particles. The different types of unit cells are based on how the particles are arranged: simple cubic, body-centered cubic, face-centered cubic, and hexagonal close-packed.

JEE Main 2025: Chemistry Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics |  PYQs

This Story also Contains

1. Packing Efficiency in HCP and CCP Structures
2. Some Solved Examples
3. Summary

Packing Efficiency in HCP and CCP Structures

Both types of close packing (hcp and ccp) are equally efficient. Let us calculate the efficiency of packing in ccp structure. In the figure, let the unit cell edge length be 'a' and face diagonal AC = b.

In $\triangle \mathrm{ABC}$

$
\begin{aligned}
& \mathrm{AC}^2=\mathrm{b}^2=\mathrm{BC}^2+\mathrm{AB}^2 \\
& =\mathrm{a}^2+\mathrm{a}^2=2 \mathrm{a}^2 \text { or } \\
& \mathrm{b}=\sqrt{2} \mathrm{a}
\end{aligned}
$
If $r$ is the radius of the sphere, we find

$
\mathrm{b}=4 \mathrm{r}=\sqrt{2 \mathrm{a}}
$

or $\mathrm{a}=\frac{4 \mathrm{r}}{\sqrt{2}}=2 \sqrt{2 \mathrm{r}}$
(We can also write, $\mathrm{r}=\frac{\mathrm{a}}{2 \sqrt{2}}$ )

As we know, that each unit cell in ccp structure, has effectively 4 spheres. Total volume of four spheres is equal to $4 \times(4 / 3) \pi \mathrm{r}^3$ and volume of the cube is $\mathrm{a}^3$ or $(2 \sqrt{2} \mathrm{r})^3$.

Therefore,

Packing efficiency $=\frac{\text { Volume occupied by four spheres in the unit cell } \times 100 \%}{\text { Total volume of the unit cell }}$

$\begin{aligned} & =\frac{4 \times(4 / 3) \pi \mathrm{r}^3 \times 100}{(2 \sqrt{2})^3} \% \\ & =\frac{(16 / 3) \pi \mathrm{r}^3 \times 100}{16 \sqrt{2} \mathrm{r}^3}=74 \%\end{aligned}$

Efficiency of Packing in Body Centred Cubic Structures

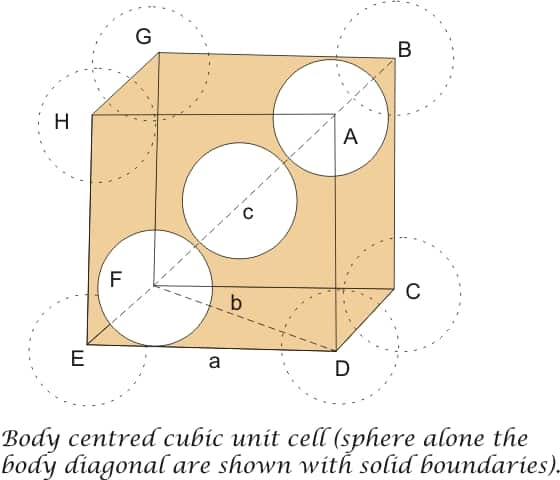
From figure, it is clear that the atom at the centre is in touch with the other two atoms diagonally arranged.

In $\triangle \mathrm{EFD}$

$
\begin{aligned}
& \mathrm{b}^2=\mathrm{a}^2+\mathrm{a}^2=2 \mathrm{a}^2 \\
& \mathrm{~b}=\sqrt{2 \mathrm{a}}
\end{aligned}
$

Now in $\triangle \mathrm{AFD}$

$
\begin{aligned}
& \mathrm{c}^2=\underline{\mathrm{a}^2+\mathrm{b}^2=\mathrm{a}^2}+2 \mathrm{a}^2=3 \mathrm{a}^2 \\
& \mathrm{c}=\sqrt{3} \mathrm{a}
\end{aligned}
$
The length of the body diagonal is equal to 4r, here is the radius of the sphere (atom), as all the three spheres along the diagonal touch each other.

So $\sqrt{3} a=3 r$

$
a=\frac{4 r}{\sqrt{3}}
$
Hence we can write, $r=\frac{\sqrt{3}}{4}$ a
In this type of structure, total number of atoms is 2 and their volume is $2 \times \frac{(4)}{3} \pi r^3$

Volume of the cube, $\mathrm{a}^3$ will be equal to $\frac{(4 r)^3}{\sqrt{3}}$ or $\mathrm{a}^3$

$
\begin{aligned}
& \text { Therefore, Packing efficiency }=\frac{\text { Volume occupied by two spheres in the unit } \times 100 \%}{\text { Total volume of the unit cell }} \\
& =\frac{4 \times(4 / 3) \pi r^3 \times 100}{\left[(4 \sqrt{3}) r^3\right.} \% \\
& =\frac{4 \times(4,3) \pi r^3 \times 100}{64 /(3 \sqrt{3}) r^3} \% \\
& =68 \%
\end{aligned}
$

Recommended topic video on (packing efficiency)

Some Solved Examples

Example 1: Which has the least packing efficiency?

1)Hcp

2)Bcc

3) Scc

4)Ccp

Solution

The packing efficiency of both HCP and CCP is 74%. The packing efficiency of BCC is 68%. Packing efficiency of SCC 52.4%.

Hence, the answer is the option (3).

Example 2: The correct order for packing fraction of different cubic systems is:

1) simple cubic < body-centered cubic < Face-centered cubic

2) face-centered cubic < simple cubic < body-centered cubic

3)face-centered cubic < body-centered cubic < simple cubic

4)body-centered cubic < simple cubic < Face-centered cubic

Solution

The packing efficiency values for different cubic systems are as follows:

• Simple cubic - 52.4%
• Body-centred cubic - 68%
• Face-centered cubic - 74%

Hence, the answer is the option (1).

Example 3: If body centred atom is removed from the BCC structure then the packing efficiency is

1)0.68

2)0.52

3) 0.34

4)0.60

Solution

Packing efficiency after removing a body-centred atom means for only one atom.

=1×43πr3(4r3)3=0.34

Hence, the answer is the option (3).

Example 4: Percentages of free space in cubic close-packed structure and in body-centred packed structure are respectively

1)48% and 26%

2)30% and 26%

3) 26% and 32%

4)32% and 48%

Solution

Packing fraction for face-centred cubic unit cell - PF = 0.74 Packing fraction for body-centered cubic unit cell - PF = 0.68

(1) Packing Efficiency in CCP is 74% and space is 26%.

(2) Packing Efficiency in BCC is 68% and space is 32%.

Hence, the answer is the option (3).

Example 5: If there are 4 atoms in one unit cell then the packing efficiency of the unit cell is:

1)0.52

2) 0.74

3)0.68

4)0.91

Solution

Packing Efficiency =z× volume of one atom volume of unit cell

Since the number of atoms per unit cell is 4 that means it is a fcc unit cell. In the fcc unit cell relation between the radius of the atom and the edge of the unit cell is given as follows:

r=a22

Thus,

Packing Efficiency =4×43πr3(22r)3=π32=0.74

Hence, the answer is (0.74).

Summary

Packing efficiency describes the density and stability of the different crystal structures. A simple cubic unit cell has a packing efficiency of about 52.4 %—just over half full. The highest packing efficiencies are achieved with the face-centered cubic and hexagonal close-packed unit cells; both are approximately 74% for a body-centered cubic unit cell, and packing efficiency is higher, at about 68%.