Algebraic Identities for Class 9 With Proofs and Examples

Algebra is a branch of mathematics that deals with variables and constants. In this process we assume the unknown quantities to be some variables from english alphabet to find out their value. In this article, we will cover the concept of all algebraic identities class 9. They carry the expressions in an equation in such a way that the left hand side of the equation is always equal to its right hand side. We will also learn about what is algebraic identities class 9, formulas for all the algebraic identities class 9 questions along with their examples and proof.

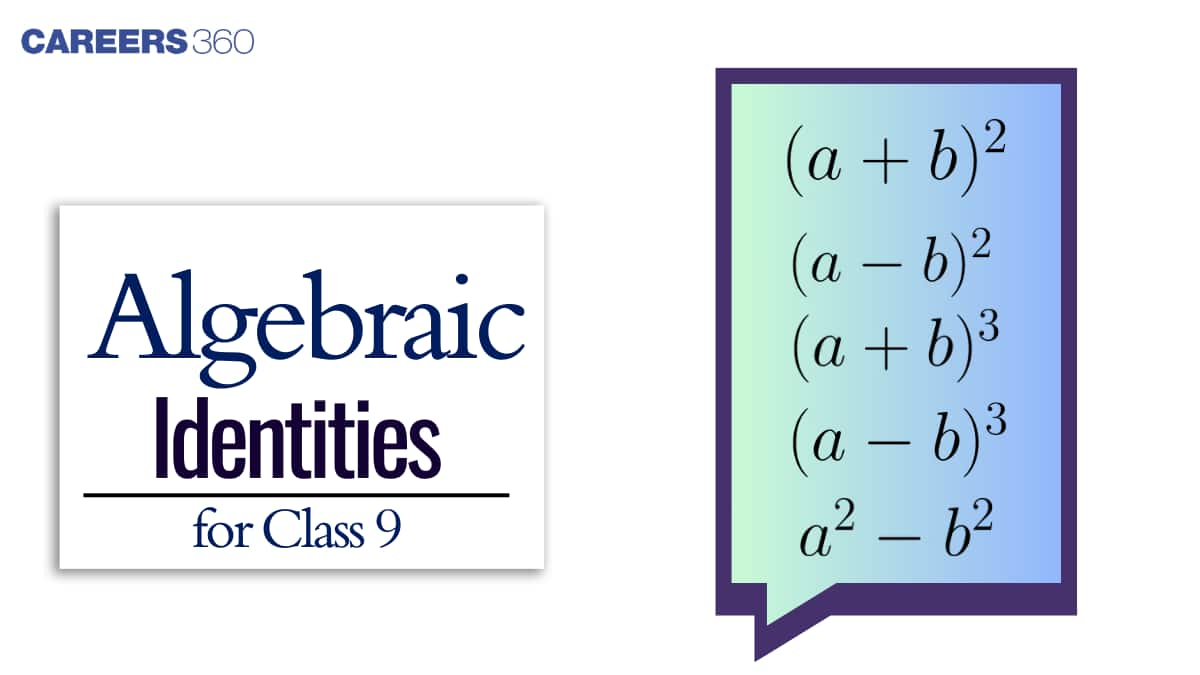
Algebraic Identities

We define identity as an equality which is true for all values of the variable. These identities are the algebraic identities, which clearly define that the (LHS) and (RHS) of the equation is equal for all the values of the variable. Algebraic expressions are usually expressed as monomials, binomials and trinomials. This description is based on the fact that how many terms are present in the expression. It may be one, two, or three. In fact, the expression which has one or more than one terms present in it is called a polynomial and the number attached to the term is called a coefficient.

Algebraic Identities Class 9 Formulas

We consider x, y and z as variables in the following identities.

Algebraic Identities for Two Variables x and y

$\begin{aligned} & (x+y)^2=x^2+y^2+2 x y \\ & (x-y)^2=x^2+y^2-2 x y \\ & x^2-y^2=(x+y)(x-y) \\ & (x+a)(x+b)=x^2+(a+b) x+a b ; a \text { and } b \text { are two constant values } \\ & (x+y)^3=x^3+y^3+3 x y(x+y) \\ & (x-y)^3=x^3-y^3-3 x y(x-y)\end{aligned}$

Algebraic Identities for Three Variables x, y and z

$\begin{aligned} & (x+y+z)^2=x^2+y^2+z^2+2 x y+2 y z+2 z x \\ & x^3+y^3+z^3-3 x y z=(x+y+z)\left(x^2+y^2+z^2-x y-y z-z x\right)\end{aligned}$

All Algebraic Identities Class 9 with proof

Identity 1: $(x+y)^2=x^2+y^2+2 x y$

Proof:

$
\begin{aligned}
& \text { L.H.S. }=(x+y)^2 \\
& =(x+y)(x+y)
\end{aligned}
$

Multiplying each term, we get,

$
\begin{aligned}
& \text { L.H.S }=x^2+x y+x y+y^2 \\
& =x^2+2 x y+y^2 \\
& \text { L.H.S }=\text { R.H.S. }
\end{aligned}
$

Identity 2: $(x-y)^2=x^2+y^2-2 x y$

Proof:
Taking L.H.S.,

$
\begin{aligned}
& (x-y)^2=(x-y)(x-y) \\
& (x-y)^2=x^2-x y-x y+y^2 \\
& (x-y)^2=x^2-2 x y+y^2
\end{aligned}
$

L.H.S. = R.H.S. Hence, proved.

Identity 3: $\mathrm{x}^2-\mathrm{y}^2=(\mathrm{x}+\mathrm{y})(\mathrm{x}-\mathrm{y})$

Proof:
Taking R.H.S and multiplying each term.

$
(x+y)(x-y)=x^2-x y+x y-y^2
$

$(x+y)(x-y)=x^2-y^2$ Hence proved

Identity 4: $(x+a)(x+b)=x^2+x(a+b)+a b$

Proof:

$
(x+a)(x+b)=x^2+x b+a x+a b=x^2+x(a+b)+a b
$

Identity 5: $(\mathrm{a}+\mathrm{b})^3=\mathrm{a}^3+\mathrm{b}^3+3 \mathrm{ab}(\mathrm{a}+\mathrm{b})$

Proof:

$
\begin{aligned}
& (a+b)^3=(a+b)(a+b)^2 \\
& =(a+b)(a^2+b^2+2 a b) \\
& =a^3+a b^2+2 a^2 b+b a^2+b^3+2 a b^2 \\
& =a^3+b^3+3 a^2 b+3 a b^2 \\
& =a^3+b^3+3 a b(a+b)
\end{aligned}
$

Identity 6: $(a-b)^3=a^3-b^3-3 a b(a-b)$

Proof:

$
\begin{aligned}
& (a-b)^3 \\
& =(a-b)(a-b)^2 \\
& =(a-b)(a^2+b^2-2 a b) \\
& =a^3+a b^2-2 a^2 b-b a^2-b^3+2 a b^2 \\
& =a^3-b^3-3 a^2 b+3 a b^2 \\
& =a^3-b^3-3 a b(a-b)
\end{aligned}
$

Identity 7: $ \cdot(a+b+c)^2=a^2+b^2+c^2+2 a b+2 b c+2 c a$

Proof:

$
\begin{aligned}
& (a+b+c)^2 \\
& =(a+b+c)(a+b+c) \\
& =a^2+a b+a c+b a+b^2+b c+c a+c b+c^2 \\
& =a^2+b^2+c^2+2 a b+2 b c+2 c a
\end{aligned}
$
Similarly, we can prove the other above given algebraic identities.

All Algebraic Identities Class 9 with Examples

Now let us look into some algebraic identities class 9 solutions for examples.

Example 1: Solve $(x+2)(x-2)$ using algebraic identities.
Solution: By the algebraic identity, $\mathrm{x}^2-\mathrm{y}^2=(\mathrm{x}+\mathrm{y})(\mathrm{x}-\mathrm{y})$, we can write the given expression as;

$
(x+2)(x-2)=x^2-2^2=x^2-4
$

Example 2: Solve $(x+7)^3$ using algebraic identities.
Solution: We know,

$
(x+y)^3=x^3+y^3+3 x y(x+y)
$

Therefore,

$
\begin{aligned}
& (x+7)^3=x^3+7^3+3 \cdot x \cdot 7(x+7) \\
& =x^3+343+21 x(x+7) \\
& =x^3+343+21 x^2+147 \\
& =x^3+21 x^2+490
\end{aligned}
$

Example 3: Expand $(2 x+9 y)^2$
Solution: Expanding the given expression, substituting $\mathrm{a}=2 \mathrm{x}$ and $\mathrm{b}=9 \mathrm{y}$ in $(\mathrm{a}+\mathrm{b})^2=\mathrm{a}^2+$ $2 a b+b^2$,

$
\begin{aligned}
& (2 x+9 y)^2=(2 x)^2+2(2 x)(9 y)+(9 y)^2 \\
& =4 x^2+36 x y+81 y^2
\end{aligned}
$

Example 4: When $\mathrm{a}+\mathrm{b}+\mathrm{c}=1$, what is the value of $\mathrm{a}^3+\mathrm{b}^3+\mathrm{c}^3$ ?
Solution: By one of the above identities,

$
a^3+b^3+c^3-3 a b c=(a+b+c)\left(a^2+b^2+c^2-a b-c a-b c\right)
$

Substituting $(a+b+c)=1$, we get

$
\begin{aligned}
& a^3+b^3+c^3-3 a b c=1\left(a^2+b^2+c^2-a b-c a-b c\right) \\
& a^3+b^3+c^3-3 a b c=\left(a^2+b^2+c^2-a b-c a-b c\right) \\
& a^3+b^3+c^3=3 a b c+\left(a^2+b^2+c^2-a b-c a-b c\right)
\end{aligned}
$

Example 5: Using identities, solve $290 \times 310$.
Solution: $290 \times 303$ can be written as $(300-10) \times(300+10)$
And this is based on the algebraic identity $(a+b)(a-b)=a^2-b^2$
Here we have $a=300$, and $b=10$
Substituting the values in the above identity, we get:

$
\begin{aligned}
& (300-10)(300+10)=300^2-10^2 \\
& =90000-100 \\
& =89900
\end{aligned}
$

List of Topics Related to Algebraic Identities Class 9