AM GM Inequality Solved Problems

AM-GM Inequality

Edited By Komal Miglani | Updated on Sep 18, 2024 04:30 PM IST

If three terms are in AP, then the middle term is called the Arithmetic Mean (A.M.) of the other two numbers. So if a, b, and c are in A.P., then b is AM of a and c. If three terms are in G.P., then the middle term is called the Geometric Mean (G.M.) of the other two numbers. So if a, b, and c are in G.P., then b is GM of a and c. In real life, we use the application of AM-GM Inequality in statistics, and economics and examine some optimization problems.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics

This Story also Contains

AM-GM Inequality
Derivation of AM-GM Inequality
AM-GM Inequality Formula
Derivation of AM-GM Inequality Formula
Application of A.M., G.M., and H.M.
Solved Examples Based on the Application of AM-GM Inequality
Summary

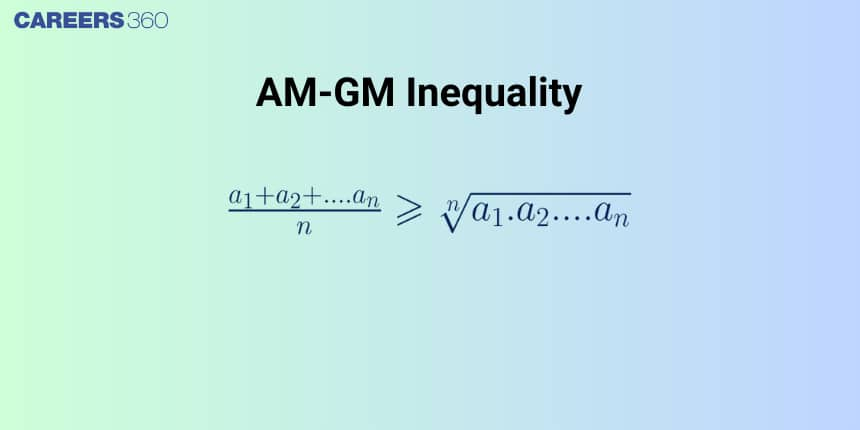
In this article, we will cover the application of AM-GM Inequality. This category falls under the broader category of sequence and series, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main Exam (from 2013 to 2023), a total of nine questions have been asked on this concept, including one in 2019, one in 2020, one in 2021, two in 2022, and three in 2023.

What is AM-GM Inequality?

Arithmetic mean - Geometric mean (AM-GM) Inequality is a fundamental result in algebra that provides a relationship between the arithmetic mean and the geometric mean of a set of non-negative real numbers. This inequality states that for any list of non-negative real numbers, the arithmetic mean (average) is at least as great as the geometric mean.

AM-GM Inequality

Case 1: If $a_1,a_2,a_3,........,a_n$ are n positive variables and k is a constant

$\\\mathrm{If\;\mathit{a_1+a_2+a_3+........+a_n=k}\;(constant),\;then\;the\;greatest\;value \;of \;}\\\mathrm{\mathit{a_1\cdot a_2\cdot a_3\cdot........\cdot a_n}\;is\;\left (\frac{k}{n} \right )^n \;and \;this\;is\;possible \;when\;\mathit{a_1=a_2=a_3=.....=a_n}}.$

Derivation of AM-GM Inequality

$\\\mathrm{as,\;AM\geq GM}\\\\\mathrm{\therefore \frac{a_1+a_2+a_3+.......+a_n}{n}\geq\left ( a_1\cdot a_2\cdot a_3\cdot .......\cdot a_n \right )^{\frac{1}{n}}}\\\mathrm{\Rightarrow \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{k}{n}\geq \left ( a_1\cdot a_2\cdot a_3\cdot .......\cdot a_n \right )^{\frac{1}{n}}}\\\mathrm{or \;\;\left ( a_1\cdot a_2\cdot a_3\cdot .......\cdot a_n \right )\leq\left (\frac{k}{n} \right )^{n}}$

AM-GM Inequality Formula

If $a_1,a_2,a_3,........,a_n$ are n positive variables and k is a constant

$\\\mathrm{If\;a_1\cdot a_2\cdot a_3\cdot \ldots\ldots\cdot a_n=k,\;where \;k\;is\;constant,\;then\,the\;value\;of\;}\\\mathrm{a_1+a_2+a_3+\ldots\ldots+a_n\;is\;minimum\;when\;all\;the\;terms\;are\;equal}\\\mathrm{\;to\;each\;other,\;i.e.\;a_1=a_2=a_3=\ldots\ldots=a_n.}\\\mathrm{So\;that\;the\;least\;value\;of\;a_1+a_2+a_3+\ldots\ldots+a_n\;is\;n(k)^{1/n}.}$

Derivation of AM-GM Inequality Formula

To prove this we will be using the fact that A.M. ≥ G.M

So,

$\\\mathit{\quad \;\frac{a_1+a_2+a_3+\ldots\ldots+a_n}{n}\geq\left ( a_1\cdot a_2\cdot a_3\cdot \ldots\ldots\cdot a_n \right )^{1/n}=k^{1/n}}\\\mathit{\Rightarrow \frac{a_1+a_2+a_3+\ldots\ldots+a_n}{n}\geq k^{1/n}}\\\mathit{\Rightarrow {a_1+a_2+a_3+\ldots\ldots+a_n}\geq n\cdot k^{1/n}}\\\mathrm{Here,\;\mathit{a_1=a_2=a_3=}\ldots\ldots=\mathit{a_n}}\\\mathit{\therefore \;least\;value\;of\;a_1+a_2+a_3+\ldots\ldots+a_n\;is\;n\cdot k^{1/n}}$

Application of A.M., G.M., and H.M.

Let A, G, and H be arithmetic, geometric, and harmonic means of two positive real numbers a and b.

Then, $\\\mathrm{A=\mathit{\frac{a+b}{2}}\;,\;\;G=\mathit{\sqrt{a\cdot b}}\;\;\;and\;\;H=\mathit{\frac{2ab}{a+b}}}$

1) A ≥ G ≥ H

$\\\mathrm{A-G=\mathit{\frac{a+b}{2}-\sqrt{ab}= \frac{\left (\sqrt{a}-\sqrt{b} \right )^2}{2}}\geq0}\\\\\mathrm{\Rightarrow A-G\geq0}\\\\\mathrm{\Rightarrow A\geq G\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;........(i)}\\$

Note that A = G when a = b

Now,

$\\\mathrm{G-H=\mathit{\sqrt{ab}-\frac{2ab}{a+b}}}\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;=\mathit{\sqrt{ab}\left ( \frac{a+b-2\sqrt{ab}}{a+b} \right )}}\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;=\mathit{\frac{\sqrt{ab}}{a+b}\left ( \sqrt{a}-\sqrt{b} \right )^2}\geq 0}\\\\\mathrm{\Rightarrow G\geq H\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;.......(ii)}\\\text{Again G=H when a = b}\\\\\mathrm{From\;(i)\;and\;(ii)\;we\;get\;}\\\mathrm{A\geq G\geq H}$

Note :

when a = b then only, A = G = H
The same relation $A\geq G\geq H$ can be applied to AM, GM, and HM of more than 2 positive real numbers

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

If $a_1, a_2, a_3, ....., a_n$ are n positive real numbers, then

A = A.M. of $a_1, a_2, a_3, ....., a_n$ = $\frac{a_1+ a_2+ a_3+ .....+a_n}{n}$

G = G.M. of $a_1, a_2, a_3, .....,a_n$ = $(a_1. a_2. a_3. ......a_n)^{\frac{1}{n}}$

H = H.M. of $a_1, a_2, a_3, ......,a_n$ = $\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+......+\frac{1}{a_n}}$

In such cases also $A\geq G\geq H$

And A=G=H, when $a_1=a_2=a_3=......=a_n$

2) A, G, and H of 2 positive real numbers form a geometric progression, i.e. G² = AH.

$\\\mathrm{we\;have,}\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;A\cdot H=\mathit{\frac{a+b}{2}\times \frac{2ab}{a+b}}}\\\\\mathrm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\mathit{ab=\left ( \sqrt{ab} \right )^2}=G^2}\\\\\mathrm{Hence,\;\;G^2=AH}$

Solved Examples Based on the Application of AM-GM Inequality

Example 1: If $f(x)=\frac{\left(\tan 1^{\circ}\right) x+\log _e(123)}{x \log _e(1234)-\left(\tan 1^{\circ}\right)}, x>0$ then the least value of $f(f(x))+f\left(f\left(\frac{4}{x}\right)\right)$ [JEE MAINS 2023]

Solution

$f(x)=\frac{\left(\tan 1\right) x+\log _e123}{x \log 1234-\left(\tan 1\right)}$

Let $A=tan1,$ $B=log123, \, \; C=LOG1234\\$

$\begin{aligned} & f(x)=\frac{A x+B}{x C-A} \\ & f(f(x))=\frac{A\left(\frac{A x+B}{x C-A}\right)+B}{C\left(\frac{A x+B}{C X-A}\right)-A} \\ & =\frac{A^2 x+A B+x B C-A B}{A C x+B C-A C x+A^2} \end{aligned}$

$=\frac{x(A^{2}+BC)}{(A^{2}+BC)}=x$

$\begin{aligned} & f(f(x))=x \\ & f\left(f\left(\frac{4}{x}\right)\right)=\frac{4}{x} \\ & f(f(x))+f\left(f\left(\frac{4}{x}\right)\right) \\ & A M \geq G M \\ & x+\frac{4}{x} \geq 4 \end{aligned}$

Hence, the answer is 4

Example 2: Let a, b, c, and d be positive real numbers such that $a+b+c+d=11$ .If the maximum value of $a^{5} b^{3} c^{2} d$ is $3750 \beta$ , then the value of $\beta$ is [JEE MAINS 2023]

Solution

$Given \: \; \mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=11 \quad$ (a, b, $c, \mathrm{~d}>0\}$

$\left(a^{5} \mathrm{~b}^{3} c^{2} d\right)max.= ?$
Let's assume Numbers –
$\frac{\mathrm{a}}{5}, \frac{\mathrm{a}}{5}, \frac{\mathrm{a}}{5}, \frac{\mathrm{a}}{5}, \frac{\mathrm{a}}{5}, \frac{\mathrm{b}}{3}, \frac{\mathrm{b}}{3}, \frac{\mathrm{b}}{3}, \frac{\mathrm{c}}{2}, \frac{\mathrm{c}}{2}$

We know A.M. $\geq$ G.M.
$\frac{\frac{a}{5}+\frac{a}{5}+\frac{a}{5}+\frac{a}{5}+\frac{a}{5}+\frac{b}{3}+\frac{b}{3}+\frac{b}{3}+\frac{c}{2}+\frac{c}{2}+d}{11} \geq\left(\frac{a^{5} b^{3} c^{2} d}{5^{5} \cdot 3^{3} \cdot 2^{2} \cdot 1}\right)^{\frac{1}{11}}$
$\frac{11}{11} \geq\left(\frac{a^{5} b^{3} c^{2} d}{5^{5} \cdot 3^{3} \cdot 2^{2} \cdot 1}\right)^{\frac{1}{11}}$

$a^{5} \cdot b^{3} \cdot c^{2} \cdot d \leq 5^{5} \cdot 3^{3} \cdot 2^{2}$

$\max \left(\mathrm{a}^{5} \mathrm{~b}^{3} \mathrm{c}^{2} \mathrm{~d}\right)=5^{5} \cdot 3^{3} \cdot 2^{2}=337500$

$=90 \times 3750=\beta \times 3750$
$\beta=90$
Hence, the answer is 90

Example 3: If the minimum value of $\mathrm{f(x)=\frac{5 x^{2}}{2}+\frac{\alpha}{x^{5}}, x>0 }$ , is $14$ , then the value of $\alpha$ is equal to : [JEE MAINS 2022]

Solution

$\begin{aligned} & \mathrm{\frac{x^{2}}{2}+\frac{x^{2}}{2}+\frac{x^{2}}{2}+\frac{x^{2}}{2}+\frac{x^{2}}{2}+\frac{\alpha}{2 x^{5}}+\frac{\alpha^{1}}{2 x^{5}}}\geq \mathrm{7\left ( \frac{\alpha ^{2}}{2^{7}} \right )^{\frac{1}{7}}} \\ & \mathrm{\frac{7 \cdot(\alpha)^{2 / 7}}{2}=14} \\ &\mathrm{\left(\alpha^{2}\right)^{1 / 7}=2^{2}} \\ &\mathrm{\alpha=\left(2^{2}\right)^{7 / 2}=2^{7} }\\ &\mathrm{\alpha=128} \end{aligned}$

Hence, the answer is 128

Example 4: Let $\mathrm{x,y>0}$ . If $\mathrm{x^{3}y^{2}=2^{15}}$ , then the least value of $\mathrm{3x+2y}$ is [JEE MAINS 2022]

Solution

$\begin{aligned} & \mathrm{x, y>0} \\ & \mathrm{x^{3} y^{2}=2^{15}} \end{aligned}$

we know that $\mathrm{A.m \geq G.m}$

$\begin{aligned} \frac{x+x+x+y+y}{5} & \mathrm{\geq\left(x^{3} y^{2}\right)^{\frac{1}{5}}} \\ \mathrm{\frac{3 x+2 y}{5}} & \mathrm{\geq 2^{3} }\\ \mathrm{3 x+2 y} & \mathrm{\geq 0} \end{aligned}$

$\therefore$ the least value of $\mathrm{3 x+2 y=40 }$

Hence, the answer is 40

Example 5: The minimum value of $2^{\sin x}+2^{\cos x}$ is: [JEE MAINS 2020]

Solution

$\\\mathrm{Apply\;AM\geq GM}$

$\\\Rightarrow \frac{2^{\sin x}+2^{\cos x}}{2}\geq\sqrt{2^{\sin x}\cdot2^{\cos x}}\\\Rightarrow {2^{\sin x}+2^{\cos x}}\geq2\sqrt{2^{\sin x+\cos x}}$

$\\ \Rightarrow 2^{\sin x}+2^{\cos x} \geq 2^{1+\left(\frac{\sin x+\cos x}{2}\right)} \\ \Rightarrow \min \left(2^{\sin x}+2^{\cos x}\right)=2^{1-\frac{1}{\sqrt{2}}}$

Hence, the answer is $2^{1-\frac{1}{\sqrt{}2}}$

Summary

The Arithmetic Mean (AM) and Geometric Mean (GM) inequalities are fundamental principles in mathematics, offering insights into the relationships between arithmetic averages and geometric averages of sets of numbers. It helps us to solve problems ranging from simpler to advanced mathematical solutions. Understanding and applying these inequalities enriches our ability to analyze and derive conclusions in mathematical reasoning and practical applications alike.

Frequently Asked Questions (FAQs)

1. How do you find the Arithmetic, Geometric, and Harmonic mean of two numbers a and b?

Let A, G, and H be arithmetic, geometric, and harmonic means of two positive real numbers a and b.

Then, $\\\mathrm{A=\mathit{\frac{a+b}{2}}\;,\;\;G=\mathit{\sqrt{a\cdot b}}\;\;\;and\;\;H=\mathit{\frac{2ab}{a+b}}}$

2. Which is greater among arithmetic, geometric, and harmonic mean?

Let A, G, and H be arithmetic, geometric, and harmonic means of two positive real numbers a and b.

Then, $\\\mathrm{A=\mathit{\frac{a+b}{2}}\;,\;\;G=\mathit{\sqrt{a\cdot b}}\;\;\;and\;\;H=\mathit{\frac{2ab}{a+b}}}$

A ≥ G ≥ H

3. Find the relations between Arithmetic, Geometric, and Harmonic mean if a=b.

The relations between Arithmetic, Geometric, and Harmonic mean if a=b is A = G = H

4. Difference between Arithmetic and Geometric mean?

If three terms are in AP, then the middle term is called the Arithmetic Mean (A.M.) of the other two numbers. So if a, b, and c are in A.P., then b is AM of a and c. whereas, If three terms are in G.P., then the middle term is called the Geometric Mean (G.M.) of the other two numbers. So if a, b, and c are in G.P., then b is GM of a and c.

5. If A, G, and H of 2 positive real numbers form a geometric progression then what is the relation between arithmetic, geometric, and harmonic mean?

If A, G, and H of 2 positive real numbers form a geometric progression, the relation between arithmetic, geometric, and harmonic mean is G² = AH.