Analytic Function

Types Of Analytic Functions

Analytic functions are of two types:

1. Real analytic function

2. Complex analytic function

Each type of these functions is infinitely differentiable and possesses different properties.

Real Analytic Function

A real analytic function is an infinitely differentiable function whose Taylor series converges to f(x) pointwise for any x in the neighborhood of any point x_0 in its domain.

T(x)=\sum_{n=0}^{\infty}\frac{f^{n}(x_0)}{n!}(x-x_0)^n

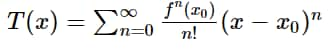
A function f(x) is a real analytic function on an open set D in the real number line if for any x0 ϵ D,

f(x)=\sum_{n=0}^{\infty}a_n(x-x_0)^n=a_0+a_1(x-x_0)+a_2(x-x_0)^2+...

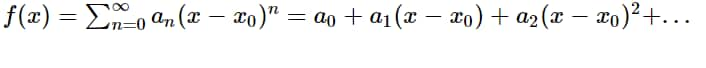
The series is convergent to f(x) for x in the neighborhood of x_0 .

The Collection of all real analytic functions on a set D is denoted by C^w(D) .

Complex Analytic Function

A function is complex analytic if and only if it is holomorphic which requires it to be complex and differentiable.

Let

f(x,y)=u(x,y)+iv(x,y)

be a complex function. Substituting x=(z+\bar z)/2 and y=(z-\bar z)/2i gives

f(z,\bar z)=u(x,y)+iv(x,y)

For f(z,\bar z) to be analytic, a necessary condition is that ∂f∂z=0.

To be analytic f=u+iv should only depend on z. Thus, real and imaginary parts u and v of f must satisfy:

\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}

\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}

The above two equations are the Cauchy-Reimann equations.

For a function to be analytical, the necessary and sufficient conditions are that the partial derivatives of real and imaginary parts \frac{\partial u}{\partial x},\frac{\partial v}{\partial y},\frac{\partial u}{\partial y},\frac{\partial v}{\partial x} must satisfy the Cauchy-Reimann equations and must be continuous.

Properties Of Analytic Functions

• Functions formed by addition, multiplication, or composition of analytic functions are also analytical.

• The limit of uniformly convergent sequences of analytic functions is also an analytic function.

• Analytic functions are infinitely differentiable.

• The function f(z)=\frac{1}{z}, z\neq 0 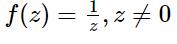is analytic.

• The modulus of the function |f(z)| cannot reach its maximum in U if f(z) is an analytic function defined on U.

• If f(z) is analytical and k is a point in its domain then the function \frac{f(z)-f(k)}{z-k} 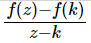is also an analytic function.

• If f(z) is an analytic function on a disk D, then there is an analytic function F(z) on D such that F’(z) = f(z). F(z) is called the primitive of f(z).

• If f(z) is an analytic function on a disk D, k is a point in the interior of the disk and C is a closed curve that does not pass through k then

W(C,k)=f(k)=\frac{1}{2\pi i}\int C\frac{f(z)-f(k)}{z-k}dz

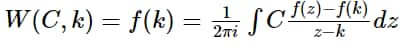
Where W(C,k) is the winding number of C around z.

• The zeroes of an analytic function are isolated points unless the function is identically zero.

• If C is a curve connecting two points z0 and z1 in the domain in the domain of an analytic function f(z) then,

\int_{c}f^{'}(z)=f(z_1)-f(z_0)

Applications Of Analytic Function

• In mathematical physics, analytic functions are crucial for solving two-dimensional problems.

• Analytic functions are used for fluid flow, electrostatic fields and heat flow problems.

Examples

Following functions are the examples of analytic functions:

• Exponential function

• Hypergeometric functions

• Trigonometric functions

• Bessel functions

• Gamma functions

• Logarithmic functions

• All polynomials