Angle Between Two Lines
When two straight lines intersect, they form two sets of angles. The intersection results in two acute angles and two obtuse angles. The absolute value of angles is determined by the slopes of intersecting lines. The angle between two lines represents the degree of inclination between the two lines and the inclination of two lines is advantageous to comprehend how the lines are associated with each other.
This Story also Contains
- The Angle Between Two Lines In Two-Dimensional Space.
- The Angle Between Two Lines In Three-Dimensional Space
- Vertically Opposite Angles And Adjacent Angles
- Examples
The Angle Between Two Lines In Two-Dimensional Space.
The angle between two lines can be computed either by knowing the slope of two lines or by knowing the equations of the two lines. Generally, the acute angle between the lines is calculated.by following methods
The angle between two lines when the slope of the lines is known.
To calculate the angle between two lines when the slope of the lines is known, the trigonometric tangent function is used. Take into consideration two lines that have slopes of m1 and m2, respectively. Using the tangent function formula, it is possible to determine the acute angle between the lines. The acute angle \theta ![]() between the lines is given by:
between the lines is given by:
\tan\theta=\frac{m1-m2}{1+m1\cdot m2}
![]()
The angle between two lines when the equations of the lines are known.
Let the equations of the lines be given by,
l_1=a_1x+b_1y+c_1\\
and \\
l_2=a_2x+b_2y+c_2
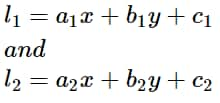
then the tangent of the acute angle between the lines can be computed by the following formula.
\tan\theta=\frac{a_2b_1-a_1b_2}{a_1a_2+b_1b_2}
![]()
If the lines are parallel, the angle between them is zero.
This gives, \tan\theta=0
![]()
\frac{m1-m2}{1+m1\cdot m2}=0
![]()
m1-m2 = 0,
And hence,
m1=m2
So, this can be concluded that the slope of two parallel lines is the same.
If the lines are perpendicular, the angle between them is 90^{\circ}
 .
.
This gives, \frac{1}{tan\theta}=0
![]()
\frac{1+m1\cdot m2}{m1-m2}=0
![]()
1+m1\cdot m2=0
![]()
m1\cdot m2=-1
![]()
So, the product of slopes of perpendicular lines is equal to -1.
Consider a pair of straight lines having the following equation:
ax^2 + 2hxy + by^2 = 0
![]()
then the angle between the pair of straight lines is given by
\tan\theta=\frac{2\sqrt{h^2-ab}}{a+b}
![]()
The Angle Between Two Lines In Three-Dimensional Space
The calculation of the angle between two lines in a three-dimensional space is similar to that of in two-dimensional space.
Consider two lines with the following equations:
r=a_1+\lambda b_1 \\ and \\ r=a_2+\lambda b_2
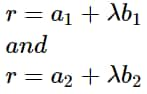
the angle between these lines is given by the formula:
\cos\theta=\frac{b_1b_2}{|b_1||b_2|}
![]()
Consider two lines having direction ratios (a_1,b_1,c_1)\: and\: (a_2,b_2,c_2)
![]()
Then the angle between the lines is given by the following formula.
\cos\theta=\frac{a_1a_2+b_1b_2+c_1c_2}{\sqrt{a_1^2+b_1^2+c_1^2}\sqrt{a_2^2+b_2^2+c_2^2}}
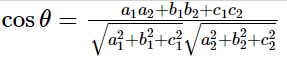
Consider two lines having the direction cosines as l_1, m_1, n_1 \: and \: l_2,m_2,n_2
then the angle between the lines is calculated by using the following formula.
\cos\theta=|l_1l_2+m_1m_2+n_1n_2|
![]()
Vertically Opposite Angles And Adjacent Angles
When two lines intersect, a pair of vertically opposite angles and a pair of adjacent angles are formed.
Pair of vertically opposite angles: (1, 3) and (2, 4)
Pair of adjacent angles: (1, 2), (2, 3), (3, 4) and (4, 1)
The measure of vertically opposite angles is equal.
\angle 1 = \angle 3\\
\angle 2 = \angle 4
![]()
The sum of two adjacent angles is equal to 180 degrees.
\angle 1 +\angle 2=180 ^{\circ}\\
\angle 2 +\angle 3=180 ^{\circ}\\
\angle 3 +\angle 4=180 ^{\circ}\\
\angle 4 +\angle 1=180 ^{\circ}
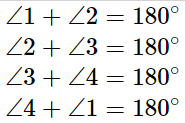
Examples
Find the measure of the acute angle between the two straight lines having slopes m1=5 and m2=4.
Using the formula, \tan\theta=\frac{m1-m2}{1+m1\cdot m2}
\tan\theta=\frac{5-4}{1+5\cdot 4}
\tan\theta=\frac{1}{21}\\
\theta=\tan^{-1}\frac{1}{21}=0.047^{\circ}
![]()
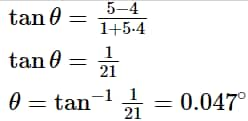
Find the measure of the acute angle between the two straight lines whose equations are x+2y+3=0 and 2x+4y+9=0.
Using the formula, \tan\theta=\frac{a_2b_1-a_1b_2}{a_1a_2+b_1b_2}
![]()
\tan\theta=\frac{2\cdot2-1\cdot4}{1\cdot2+2\cdot4}\\
\tan\theta=\frac{0}{10}=0\\
\theta=0^{\circ}
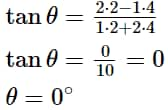
Frequently Asked Questions (FAQs)
The calculation of the angle between two straight lines can be used to find the angle of a polygon.
when two lines intersect, a pair of vertically opposite angles and a pair of adjacent angles are formed.The measure of vertically opposite angles is the same.
The sum of two adjacent angles is equal to 180 degrees.
The angle between two parallel lines is equal to zero.
The angle between two lines can be determined by using either the slope of the lines or the equation of the lines.
If the slope of two straight lines is m1 and m2 then the acute angle between them is given by:
\tan\theta=\frac{m1-m2}{1+m1\cdot m2}
![]()
If the equation of the two straight lines are
l_1=a_1x+b_1y+c_1\\
and \\
l_2=a_2x+b_2y+c_2
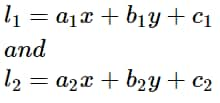
Then the acute angle between them is given by the following formula:
\tan\theta=\frac{a_2b_1-a_1b_2}{a_1a_2+b_1b_2}
![]()