Angle Between Two Planes in 3D

The angle between two Planes is determined by the angle between the normals of the two planes. It is also called dihedral angles. It can be determined by the vector form and cartesian form from the equation of the plane. In real life, we use the angle between two planes for engineering construction, bridges, houses, etc.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is the Angle Between Two Planes?
2. Equation of the Angle Between Two Planes in Vector Form
3. Equation of the Angle Between Two Planes in Cartesian Form
4. Condition for Perpendicularity of Two Planes
5. If the planes are at right angles, then $\theta=90^{\circ}$ and so $\cos \theta=0$. Hence, $\cos \theta=a_1 a_2+b_1 b_2+c_1 c_2=0$Condition for Parallelism of Two Plane
6. Solved Examples Based on Angle Between Two Planes
7. Summary

In this article, we will cover the concept of Angle Between Two Planes. This topic falls under the broader category of Three Dimensional Geometry, which is a crucial chapter in Class 12 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of eight questions have been asked on this topic in JEE Main from 2013 to 2023 including one in 2021, four in 2022, and two in 2023.

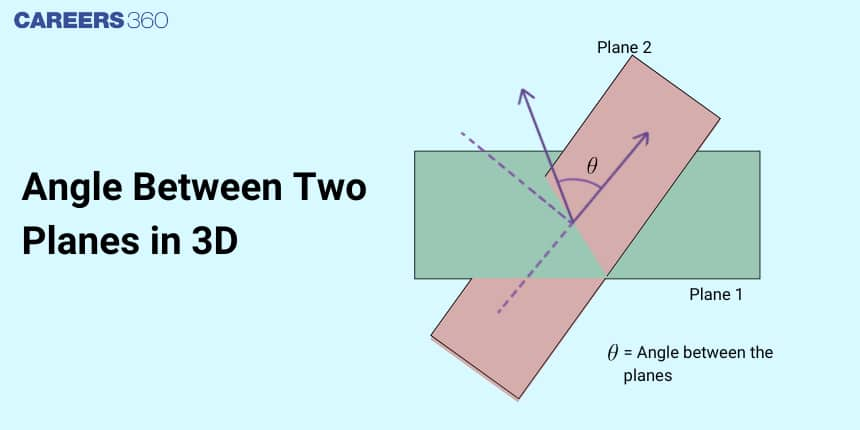
What is the Angle Between Two Planes?

The angle between two planes is defined as the angle between the normals of the two planes. It is also called dihedral angles. The angle between two planes is generally calculated with the knowledge of the angle between their normal. In other words, the angle between normal of two planes is the angle between the two planes.

Equation of the Angle Between Two Planes in Vector Form

Let $\theta$ be the angle between two planes $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_1=\mathbf{d}_1$ and $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_2=\mathbf{d}_2$ then,

$
\cos \theta=\frac{\overrightarrow{\mathbf{n}}_1 \cdot \overrightarrow{\mathbf{n}}_2}{\left|\overrightarrow{\mathbf{n}}_1\right|\left|\overrightarrow{\mathbf{n}}_1\right|}
$

Condition for Perpendicularity of Two Plane

If the planes $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_1=\mathbf{d}_1$ and $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_2=\mathbf{d}_2$ are perpendicular, then $\overrightarrow{\mathbf{n}}_1$ and $\overrightarrow{\mathbf{n}}_2$ are perpendicular.

Therefore $\overrightarrow{\mathbf{n}}_1 \cdot \overrightarrow{\mathbf{n}}_2=0$.

Condition for Parallelism of Two Plane

If the planes $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_1=\mathbf{d}_1$ and $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_2=\mathbf{d}_2$ are parallel, then there exists a scalar $\lambda$ such that $\overrightarrow{\mathbf{n}}_1=\lambda \overrightarrow{\mathbf{n}}_2$.

Equation of the Angle Between Two Planes in Cartesian Form

Let $\theta$ be the angle between the planes, $a_1 x+b_1 y+c_1 z+d_1=0$ and $a_2 x+$ $b_2 y+c_2 z+d_2=0$

Then,

$
\cos \theta=\left|\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}\right|
$

The direction ratios of the normal to the planes are $a_1, b_1, c_1$, and $a_2, b_2$ $\mathrm{c}_2$ respectively.

Condition for Perpendicularity of Two Planes

If the planes are at right angles, then $\theta=90^{\circ}$ and so $\cos \theta=0$. Hence, $\cos \theta=a_1 a_2+b_1 b_2+c_1 c_2=0$
Condition for Parallelism of Two Plane

If the planes are parallel, then $\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

Recommended Video Based on Angle Between Two Planes

Solved Examples Based on Angle Between Two Planes

Example 1: Let $\theta$ be the angle between the planes and $P_1: \vec{r} \cdot(\hat{\imath}+\hat{\jmath}+2 \hat{k})=9$ and $P_2: \vec{r} \cdot(2 \hat{\imath}-\hat{\jmath}+\hat{k})=15$ Let L be the line that meets $P_2$ at the point $(4,-2,5)$ and makes an angle $\theta$ with the normal of $P_2$. If a is the angle between L and $P_2$, then $(\tan 2 \theta)(\cot 2 \alpha)$ is equal to
[JEE MAINS 2023]

Solution

$
\begin{aligned}
& \cos \theta=\frac{\langle 1,1,2\rangle \cdot\langle 2,-1,1\rangle}{6} \\
& =\frac{2-1+2}{6}=\frac{1}{2} \\
& \theta=\frac{\pi}{3}
\end{aligned}
$

then $\frac{\pi}{2}-\alpha=\frac{\pi}{3}$

$\begin{gathered}
\alpha=\frac{\pi}{6} \\
\left(\tan ^2 \theta\right)\left(\cot ^2 \alpha\right)=(\sqrt{3})^2 \times(\sqrt{3})^2=9
\end{gathered}
$

Hence, the answer is 9

Example 2: If $\lambda_1<\lambda_2$ are two values of $\lambda$ such that the angle between the planes $P_1: \overrightarrow{\mathrm{r}} \cdot(3 \hat{\imath}-5 \hat{\jmath}+\hat{\mathrm{k}})=7$ and $P_2: \vec{r} \cdot(\lambda \hat{\imath}+\hat{\jmath}-3 \hat{k})=9$ is $\sin ^{-1}\left(\frac{2 \sqrt{6}}{5}\right)$ then the square of the length of perpendicular from the point $\left(38 \lambda_1, 10 \lambda_2, 2\right)$ to the plane $P_1$ is
[JEE MAINS 2023]

Solution:
Plane
$
\begin{aligned}
& P_1: \vec{r} \cdot(3 \hat{i}-5 \hat{j}+\hat{k})=7 \\
& P_2: \vec{r} \cdot(\lambda \hat{i}+\hat{j}-3 k)=9
\end{aligned}
$

the angle between planes is the same as the angle between their normal. the angle between normal is

$
\begin{aligned}
& \operatorname{Cos} \theta=\frac{\langle 3,-5,1\rangle \cdot\langle\lambda, 1,-3\rangle}{\sqrt{9+25+1} \sqrt{\lambda^2+1+9}} \\
& \operatorname{Cos} \theta=\frac{3 \lambda-5-3}{\sqrt{35} \sqrt{\lambda^2+10}} \\
& \because \quad \theta=\sin ^{-1}\left(\frac{2 \sqrt{6}}{5}\right) \text { then } \\
& \sin \theta=\frac{2 \sqrt{6}}{5} \\
& \cos \theta=\frac{1}{5}
\end{aligned}
$

from equation (1)

$\begin{aligned} & \frac{3 \lambda-8}{\sqrt{35} \sqrt{\lambda^2+10}}=\frac{1}{5} \\ & \Rightarrow \frac{(3 \lambda-8)^2}{35\left(\lambda^2+10\right)}=\frac{1}{25} \\ & \Rightarrow 5(3 \lambda-8)^2=7\left(\lambda^2+10\right) \\ & \Rightarrow 5\left(9 \lambda^2-48 \lambda+64\right)=7 \lambda^2+70 \\ & \Rightarrow 38 \lambda^2-240 \lambda+250=0 \\ & \Rightarrow 19 \lambda^2-120 \lambda+125=0 \\ & \Rightarrow \lambda=5, \frac{25}{19} \\ & \lambda_1=\frac{25}{19}, \lambda_2=5 \\ & \operatorname{Point}\left(38 \lambda_1, 10 \lambda_2, 2\right) \equiv(50,50,2)\end{aligned}$

distance of $(50,50,2)$ from plane $P_1$ is

$
\begin{aligned}
& \mathrm{d}=\left|\frac{3 \times 50-5 \times 50+2-7}{\sqrt{9+25+1}}\right| \\
& \mathrm{d}=\left|\frac{150-250+2-7}{\sqrt{35}}\right| \\
& d=\left|\frac{105}{\sqrt{35}}\right| \\
& d=3 \sqrt{35} \\
& d^2=315
\end{aligned}
$

Hence, the answer is 315

Example 3: A plane E is perpendicular to the two planes $2 x-2 y+z=0$ and $x-y+2 z=4$, and passes through the point $\mathrm{P}(1,-1,1)$. If the distance of the plane E from the point $\mathrm{Q}(\mathrm{a}, \mathrm{a}, 2)$ is $3 \sqrt{2}$, then $(\mathrm{PQ})^2$ is equal to
[JEE MAINS 2022]

Solution

Normal $\tilde{n}$ to plane is $\tilde{n}_1 \times \overrightarrow{n_2}$

$
\begin{aligned}
& =\left|\begin{array}{rrr}
i & j & k \\
2 & -2 & 1 \\
1 & -1 & 2
\end{array}\right| \\
& =(-4+1) \mathrm{i}-(4-1) \mathrm{j}+(-2+2) \mathrm{k} \\
& =-3 \mathrm{i}-3 \mathrm{j}
\end{aligned}
$

The equation of the required plane through $\mathrm{P}(1,-1,1)$ is

$
\begin{aligned}
& -3(\mathrm{x}-1)-3(\mathrm{y}+1)+0(\mathrm{z}-1)=0 \\
& \Rightarrow \quad \mathrm{x}-1+\mathrm{y}+1=0 \\
& \Rightarrow \mathrm{x}+\mathrm{y}=0
\end{aligned}
$

Distance from $\mathrm{Q}(\mathrm{a}, \mathrm{a}, 2)$

$
\begin{aligned}
& \frac{|\mathrm{a}+\mathrm{a}|}{\sqrt{2}}=3 \sqrt{2} \\
& \Rightarrow(\mathrm{a})=3
\end{aligned}
$

$\begin{aligned} & \Rightarrow \mathrm{a}= \pm 3 \\ & \therefore \quad \mathrm{Q} \text { is }(3,3,2) \text { or }(-3,-3,2) \\ & \therefore \mathrm{PQ}^2=(3-1)^2+(3+1)^2+(2-1)^2 \\ & =4+16+1 \\ & =21\end{aligned}$

Hence, the answer is 21

Example 4: Let $P$ be the plane containing the straight line

$
\frac{x-3}{9}=\frac{y+4}{-1}=\frac{z-7}{-5}
$ and perpendicular to the plane containing the straight lines $\frac{\mathrm{x}}{2}=\frac{\mathrm{y}}{3}=\frac{\mathrm{z}}{5}$ and $\frac{\mathrm{x}}{3}=\frac{\mathrm{y}}{7}=\frac{\mathrm{z}}{8}$. If d is the distance of P from the point $(2,-5,11)$, then $\mathrm{d}^2$ is equal to:
[JEE MAINS 2022]

$
\begin{aligned}
& \text { Solution: } a(x-3)+b(y+4)+c(z-7)=0 \\
& p: 9 a-b-5 c=0 \\
& -11 a-b+5 c=0
\end{aligned}
$

After solving DR's $\alpha(1,-1,2)$
Equation of plane,

$
\begin{aligned}
& x-y+2 z=21 \\
& d=\frac{8}{\sqrt{6}} \\
& d^2=\frac{32}{3}
\end{aligned}
$

Hence, the answer is 32/3

Example 5: Let the points on the plane $P$ be equidistant from the points $(-4,2,1) \$$ and $(2,-2,3)$. Then the acute angle between the plane $P$ and the plane $2 \mathrm{x}+\mathrm{y}+3 \mathrm{z}$ is:
[JEE MAINS 2022]

Solution:
$\mathrm{A}:(-4,2,1) \quad \mathrm{B}:(2,-2,3)$
midpoint of $\mathrm{A} \& \mathrm{~B}=(-1,0,2)$
Normal vector: $\mathrm{AB}=(6,-4,2)$
$\therefore \quad \mathrm{P}^{\prime}: 6(\mathrm{x}+1)+(-4)(\mathrm{y}-0)+2(\mathrm{z}-2)=0$
$3 x-2 y+z+1=0$
P: $\quad 2 \mathrm{x}+\mathrm{y}+3 \mathrm{z}-1=0$

Angle between

$
\begin{aligned}
&\mathrm{P} \& \mathrm{P}^{\prime}=(\theta)=\cos ^{-1}\left(\frac{6-2+3}{14}\right)=\cos ^{-1}\left(\frac{1}{2}\right) \\
& \text { } \\
& =\frac{\pi}{3}
\end{aligned}
$

Hence, the answer is $\frac{\pi}{3}$

Summary

The angle between normal of two planes is the angle between the two planes. The concept of the angle between two planes increases our geometric understanding and has applications in diverse fields such as engineering, architecture, and physics. It allows for precise measurement and interpretation of orientation. Mastering the calculation and interpretation of the angle between two planes helps us in problem-solving in both theoretical and applied contexts.