Area of Hollow Cylinder: Total & Lateral Surface Area with Formula

Edited By Team Careers360 | Updated on Jul 02, 2025 05:32 PM IST

A cylinder is a three-dimensional solid object that has two bases that are both exactly circular and are connected by a curved surface that is offset from the centre. Batteries, water bottles, gas cylinders, pipes, etc. are examples of cylinders in daily life. A hollow cylinder's area can either refer to the cylinder's flat top surface or its curved top surface.

This Story also Contains

Cylinder
Type Of Cylinder
Hollow Cylinder
Volume Of A Hollow Cylinder
Area Of A Hollow Cylinder
Lateral Surface Area Of A Hollow Cylinder
Total Surface Area Of A Hollow Cylinder

Cylinder

Geometry includes dimensions, sizes, angles, shapes, and many other concepts that we encounter every day. In plane geometry, common shapes like squares, rectangles, circles, triangles, and others are flat and two-dimensional. The term "solid shape" in solid geometry refers to shapes that appear to have a three-dimensional structure, such as a sphere, cube, cuboid, cone, Cylinder etc.

A cylinder is a 3D solid shape made up of two parallel bases that are identical to one another and are connected by a curved surface. These bases resemble discs in shape. The axis of the cylinder shape is created by drawing a line through the centre or connecting the centres of two circular bases. Height, abbreviated as "h," is the angle between the two bases. The radius of the cylinder abbreviated as "r," is the distance between the centres of the two circular bases. The cylinder is composed of two circles and a rectangle. Let's look at the image below.

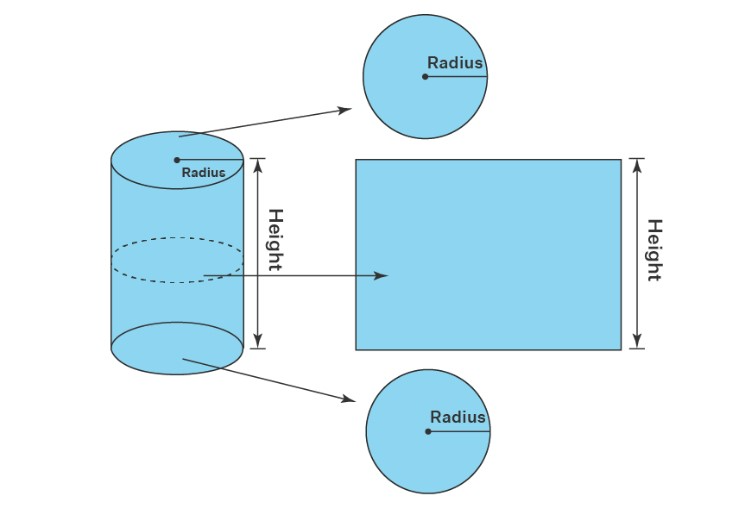
1707740891299

Type Of Cylinder

Majorly there are four different types of cylinders in geometry and they are:

Right Circular Cylinder: Right circular cylinder is the cylinder in which the axis of the two parallel bases is perpendicular to the centre of the base.
Oblique Cylinder: An oblique cylinder is a cylinder in which one side leans over the base and the sides are not perpendicular to the centre of the base. One of the real-life examples of oblique cylinders is The Leaning Tower of Pisa.
Elliptic Cylinder: An Elliptic Cylinder is a cylinder whose base is in the form of an ellipse.
Right Circular Hollow Cylinder: This is also known as Cylindrical Shell, this Cylinder consists of two right circular cylinders bounded one inside the other. The point of the axis is the same and is perpendicular to the central base. It is different from the other cylinder because it is hollow, i.e. there is some void present inside it.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Hollow Cylinder

A hollow cylinder can be defined as a type of cylinder which is vacant or empty from the inside. Or A cylinder that has some difference between the internal and external radius and is empty on the inside is said to be hollow. In other words, it is a cylindrical shape with some thickness at the edges and no interior. Some of real-life examples of hollow cylinders are, pipes, straws, pen-pencil holders, food or drink can, etc. An image of a hollow cylinder is given below.

Volume Of A Hollow Cylinder

A three-dimensional object with a circular base, the cylinder. A cylinder can be visualized as a collection of stacked circular discs. While a hollow cylinder is characterized as having a difference between the internal and external radii and being empty on the inside.

When the hollow cylinder's outer and inner radii are known, its volume can be calculated as follows:

Volume of the hollow cylinder, V = π (R2 - r2)h units3

Here,

R = outer radius of the given hollow cylinder.

r = inner radius of the given hollow cylinder.

h = height of the given hollow cylinder.

Area Of A Hollow Cylinder

The area of a hollow cylinder in two dimensions is the surface area covered by its walls. This 2D property of any geometric figure, whether 2D or 3D, exists. There are many types of surface area depending on the part of the hollow cylinder we examine.

Lateral Surface Area Of A Hollow Cylinder

The lateral surface area of the hollow cylinder is constituted of the inner surface area and the outer surface area together. It is also known as the curved surface area of the hollow cylinder because only the curved surfaces are considered.

Let the Outer radius of the hollow cylinder is ‘R’ and the inner radius of the hollow cylinder be ‘r’

Then, the lateral surface area of the hollow cylinder is : ${"mathml":"<math style=\"font-family:stix;font-size:16px;\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mstyle mathsize=\"16px\"><mn>2</mn><mi>π</mi><mfenced><mrow><mi>R</mi><mo>+</mo><mi>r</mi></mrow></mfenced><mi>h</mi></mstyle></math>","truncated":false}$

Total Surface Area Of A Hollow Cylinder

The total surface area of a hollow cylinder is the total area that a hollow cylinder is capable of having. In other words, the total surface area of the hollow cylinder is obtained by adding the area of the curved surface to the areas of the two bases.

Given that the bases, in this case, are merely a ring, we can use the cross-section calculation to get their area. However, we should be aware that since a hollow cylinder has two bases, we must double-add this cross-sectional area.

Let the Outer radius of the hollow cylinder is ‘R’ and the inner radius of the hollow cylinder be ‘r’

The Total surface area= ${"mathml":"<math style=\"font-family:stix;font-size:16px;\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mstyle mathsize=\"16px\"><mn>2</mn><mi>π</mi><mo> </mo><mfenced><mrow><mi>R</mi><mo>+</mo><mi>r</mi></mrow></mfenced><mi>h</mi><mo>+</mo><mn>2</mn><mi>π</mi><mo> </mo><mfenced><mrow><msup><mi>R</mi><mn>2</mn></msup><mo>-</mo><msup><mi>r</mi><mn>2</mn></msup></mrow></mfenced></mstyle></math>","truncated":false}$

Frequently Asked Questions (FAQs)

1. Define Hollow cylinder.

A hollow cylinder is hollow from the inside out and has a difference between its internal and external radii. The bottom of the hollow cylinder contains the region bounded by two concentric circles. A solid cylinder has an external surface that is curved. One way to picture it is as a bunch of circles stacked on top of one another. Cylinders come in two varieties: solid cylinders and hollow cylinders. If the cylinder looks to be made up of complete circles with no gaps between them, it is referred to as a solid cylinder or just a cylinder. A cylinder is described as hollow if it looks to be constructed of round rings.

2. What are real-life examples of hollow cylinders?

Some real-life examples of hollow cylinders are: Glass, Cups, pipes, straws, etc.

3. The lateral surface area of the hollow cylinder is 400 sq. unit. If we cut this hollow cylinder along its height and form a rectangle of breadth 10 units. Find the perimeter of the rectangular sheet.

We know that the Area of the Rectangular Sheet will be equal to the Surface Area of the Cylinder and the area of the Rectangle is length x breadth, thus we can write,

⇒ length x breadth = 400

⇒ length x 10 = 400

⇒ length = 40 units

And the Perimeter of the rectangle will be = 2(length + breadth)

= 2 (40 + 10)

= 100 unit

Thus, the perimeter of the rectangle is 100 units.

4. What is a hollow cylinder's cross-sectional area?

The cross-section of a hollow cylinder consists of the two pieces at its ends, which are bounded by two concentric circles. Concentric circles are circles that resemble rings. Thus, the cross-sectional area of the hollow cylinder is used to define its thickness of the hollow cylinder.

5. How Does Doubling the Height Affect the Volume of a Hollow Cylinder?

The height of a hollow cylinder determines its volume in a direct proportion. As a result, when the height of the hollow cylinder doubles, the volume also doubles.

6. Why do we subtract r² from R² in the formula for the circular ends of a hollow cylinder?

We subtract r² from R² (π(R² - r²)) to calculate the area of the circular ring at each end of the hollow cylinder. This ring is the difference between the area of the larger circle (πR²) and the smaller circle (πr²) that forms the hole.

7. How does the ratio of outer to inner radius affect the surface area of a hollow cylinder?

As the ratio of outer to inner radius increases (i.e., as the cylinder becomes thicker), the surface area increases. This is because there's more material in the walls of the cylinder, leading to larger curved surfaces and larger circular rings at the ends.

8. In what situations might calculating the surface area of a hollow cylinder be important in real life?

Calculating the surface area of a hollow cylinder can be important in various real-life situations, such as:

9. How does the concept of surface area for a hollow cylinder relate to other 3D shapes?

The concept of surface area for a hollow cylinder combines ideas from simpler shapes. The lateral surface area is related to the area of a rectangle (if "unwrapped"), while the circular ends relate to the area of a circle. This approach of breaking down complex shapes into simpler components is used for many 3D shapes.

10. If you have a solid cylinder and drill a hole through its center, how would you calculate the new surface area?

To calculate the new surface area after drilling, you'd use the hollow cylinder formulas. The original outer radius becomes R, the radius of the drilled hole becomes r, and the length of the cylinder is h. Then apply the total surface area formula: 2πh(R + r) + 2π(R² - r²).

11. What is a hollow cylinder?

A hollow cylinder is a three-dimensional object with two circular bases and a hollow interior. It's like a pipe or a tube, with an outer radius and an inner radius. The space between the outer and inner surfaces forms the body of the hollow cylinder.

12. What real-world objects can be modeled as hollow cylinders?

Many objects can be modeled as hollow cylinders, including:

13. Can the formulas for hollow cylinder surface area be applied to tapered cylinders?

The standard formulas for hollow cylinder surface area assume a constant radius. For tapered cylinders (where the radius changes along the height), you'd need to use more advanced calculus techniques, specifically integration, to calculate the surface area accurately.

14. How does the concept of hollow cylinder surface area extend to more complex shapes like hollow spheres?

The concept extends similarly, but the formulas are different. For a hollow sphere, you'd consider the outer and inner surface areas, which are 4πR² and 4πr² respectively. The total surface area would be the sum of these: 4π(R² + r²). The approach of considering both outer and inner surfaces is similar to that of hollow cylinders.

15. How would you explain the concept of hollow cylinder surface area to someone who only understands 2D shapes?

You could explain it by relating it to 2D shapes they know:

16. How do you calculate the lateral surface area of a hollow cylinder?

The lateral surface area of a hollow cylinder is calculated using the formula:

17. Why do we add the outer and inner radii in the lateral surface area formula?

We add the outer and inner radii (R + r) because we're calculating the area of both the outer and inner curved surfaces. The outer surface has a larger circumference (2πR), while the inner surface has a smaller circumference (2πr). Adding them gives us the total circumference of both surfaces.

18. What happens to the surface area if the inner radius of a hollow cylinder approaches the outer radius?

As the inner radius approaches the outer radius, the hollow cylinder becomes thinner, like a sheet rolled into a tube. The lateral surface area will decrease slightly, but the total surface area will decrease more significantly because the area of the circular rings at the ends (R² - r²) will approach zero.

19. Can the surface area of a hollow cylinder ever be zero?

No, the surface area of a hollow cylinder cannot be zero as long as it exists as a three-dimensional object. Even if the height or the difference between outer and inner radii approaches zero, there will always be some surface area.

20. How does the surface area of a hollow cylinder compare to that of a solid cylinder with the same outer dimensions?

The hollow cylinder will have a larger surface area than a solid cylinder with the same outer dimensions. This is because the hollow cylinder has an additional inner surface that contributes to its total surface area.

21. How is the area of a hollow cylinder different from a solid cylinder?

The area of a hollow cylinder includes both the outer and inner surfaces, while a solid cylinder only has an outer surface. This means we need to consider both the outer and inner radii when calculating the surface area of a hollow cylinder.

22. What are the key components needed to calculate the surface area of a hollow cylinder?

To calculate the surface area of a hollow cylinder, you need:

23. What is the difference between total surface area and lateral surface area of a hollow cylinder?

The total surface area includes all surfaces of the hollow cylinder: the outer curved surface, the inner curved surface, and the top and bottom circular rings. The lateral surface area only includes the curved surfaces (outer and inner), excluding the top and bottom.

24. What is the formula for the total surface area of a hollow cylinder?

The total surface area of a hollow cylinder is given by the formula:

25. How does changing the height of a hollow cylinder affect its surface area?

Increasing the height of a hollow cylinder will increase both its lateral and total surface area proportionally. The height is directly proportional to the surface area, so doubling the height will double the lateral surface area and increase the total surface area (though not exactly double due to the circular ends).

26. Can you have a negative surface area for a hollow cylinder?

No, it's impossible to have a negative surface area for any real, physical object, including a hollow cylinder. Surface area is a measure of the amount of surface, which is always positive in the real world. Even as dimensions approach zero, the surface area would approach zero, but never become negative.

27. How does the surface area of a hollow cylinder relate to its moment of inertia?

While surface area and moment of inertia are different properties, they're both affected by the cylinder's dimensions. A larger surface area often correlates with a larger moment of inertia, as both increase with larger radii. However, the moment of inertia depends more heavily on how the mass is distributed from the axis of rotation, while surface area only depends on the dimensions.

28. How does the concept of hollow cylinder surface area apply in fluid dynamics?

In fluid dynamics, the surface area of a hollow cylinder is important for calculating:

29. If you have two hollow cylinders with the same surface area, can you conclude anything about their volumes?

Having the same surface area doesn't necessarily mean the cylinders have the same volume. They could have different combinations of height, inner radius, and outer radius that result in the same surface area but different volumes. To determine volume, you'd need more specific information about the dimensions.

30. How does the surface area to volume ratio of a hollow cylinder change as it gets larger (with proportional dimensions)?

As a hollow cylinder gets larger with proportional dimensions, its surface area to volume ratio decreases. This is because volume increases with the cube of linear dimensions, while surface area increases with the square. This principle, known as the square-cube law, applies to many geometric shapes and has important implications in biology and engineering.

31. How would you calculate the volume of material used to make a hollow cylinder, given its surface area?

To calculate the volume of material, you'd need additional information beyond just the surface area. If you know the thickness of the cylinder wall, you could multiply the lateral surface area by the thickness and add the volume of the two circular rings at the ends.

32. How does the surface area to volume ratio of a hollow cylinder compare to that of a solid cylinder?

A hollow cylinder generally has a higher surface area to volume ratio than a solid cylinder of the same outer dimensions. This is because hollowing out the cylinder increases the surface area (by adding an inner surface) while decreasing the volume.

33. How would you approach finding the surface area of a hollow cylinder if only given its volume and one radius?

This is a complex problem that requires setting up and solving a system of equations. You'd use the volume formula for a hollow cylinder (π(R² - r²)h) and the surface area formula, substituting the known radius and volume. This would give you two equations with two unknowns, which you could then solve.

34. How would you find the thickness of a hollow cylinder given its surface area and height?

To find the thickness, you'd need both the surface area and height, as well as either the inner or outer radius. Then you can set up the surface area equation and solve for the unknown radius. The thickness would be the difference between the outer and inner radii.

35. What's the significance of π in the surface area formulas for a hollow cylinder?

π (pi) appears in the formulas because it's fundamental to calculating the circumference and area of circles. In a cylinder, π is used to calculate the circumference of the circular bases (2πr) and the areas of the circular ends (πr²). It's a constant that relates the diameter of a circle to its circumference.

36. If the outer radius of a hollow cylinder is doubled, how does it affect the surface area?

Doubling the outer radius will significantly increase the surface area. The lateral surface area will more than double because it depends on (R + r). The total surface area will increase even more dramatically because it includes terms with R² in the formula for the circular ends.

37. Is it possible for a hollow cylinder to have more lateral surface area than total surface area?

No, it's not possible. The total surface area always includes the lateral surface area plus the areas of the two circular rings at the ends. Therefore, the total surface area will always be greater than the lateral surface area.

38. What's the relationship between the surface area and the amount of paint needed to cover a hollow cylinder?

The amount of paint needed is directly proportional to the surface area. If you're painting both the inside and outside, you'd use the total surface area. If only painting the outside, you'd use the outer lateral surface area plus the areas of the outer circular rings at the ends.

39. How does the surface area of a hollow cylinder change if you "unwrap" it into a flat sheet?

If you could "unwrap" a hollow cylinder, the lateral surface area would remain the same, as it would form two rectangles (from the inner and outer surfaces). However, the total surface area would decrease slightly because you'd lose the areas of the circular rings at the ends.

40. In what ways might understanding hollow cylinder surface area be useful in engineering or architecture?

Understanding hollow cylinder surface area is crucial in engineering and architecture for:

41. What common mistakes do students make when calculating the surface area of a hollow cylinder?

Common mistakes include:

42. How does the surface area of a hollow cylinder change if you cut it in half lengthwise?

If you cut a hollow cylinder in half lengthwise:

43. How does the concept of significant figures apply to calculating hollow cylinder surface area?

When calculating surface area, the result should not be more precise than the least precise measurement used in the calculation. For example, if you're given measurements to two decimal places, your final answer should also be to two decimal places. This ensures that the calculated result doesn't imply more precision than the original data supports.

44. What's the difference between πr² and π(R² - r²) in the context of hollow cylinders?

πr² represents the area of a full circle with radius r. In contrast, π(R² - r²) represents the area of a circular ring - the difference between a larger circle of radius R and a smaller circle of radius r. This latter term is used for the end areas of a hollow cylinder, representing the material between the outer and inner radii.

45. How would you find the ratio of lateral surface area to total surface area for a hollow cylinder?

To find this ratio:

46. If you increase both the inner and outer radii of a hollow cylinder by the same amount, how does it affect the surface area?

If both radii increase by the same amount:

47. Can the surface area of a hollow cylinder ever be equal to its volume?

While it's theoretically possible for the numerical values of surface area and volume to be equal for specific dimensions, they would be expressed in different units (square units for area, cubic units for volume). In practice, this equality is rare and doesn't have physical significance due to the different dimensions of the quantities.

48. How would you approach optimizing the surface area of a hollow cylinder for a given volume?

Optimizing surface area for a given volume involves calculus, specifically optimization problems. You would:

49. What's the relationship between the surface area of a hollow cylinder and its weight?

The surface area and weight of a hollow cylinder are related, but not directly proportional. The weight depends on the volume of material and its density, while surface area depends only on dimensions. However, for cylinders made of the same material with constant wall thickness, a larger surface area generally indicates more material and thus more weight.

50. Can you use the hollow cylinder surface area formula for a cylinder with very thin walls?

Yes, the formula remains valid for cylinders with very thin walls. However, as the wall thickness approaches zero (i.e., as the inner radius approaches the outer radius), you might encounter computational issues due to rounding errors. In such cases, it might be more practical to approximate the cylinder as a single curved surface with negligible thickness.

51. How would you calculate the amount of material saved by making a cylinder hollow instead of solid?

To calculate the material saved: