Surface Area of Sphere (Formula & Solved Examples)
A sphere is a three dimensional figure in geometry that looks like a circle. It has no corners and has a smooth surface. We can define the surface area of sphere as the region covered by its outer surface in 3-D plane. In other words, we can explain it as the area covered by the sphere in xyz plane. It is found most commonly around us in the form of celestial bodies like planets, sun, moon, etc. Various daily life objects include football, basketball, etc. In this article we will learn about what is a sphere, total surface area of sphere, lateral surface area of sphere, volume and surface area of sphere and much more.
This Story also Contains
- Surface Area of Sphere
- Volume of Sphere
- Solved Examples
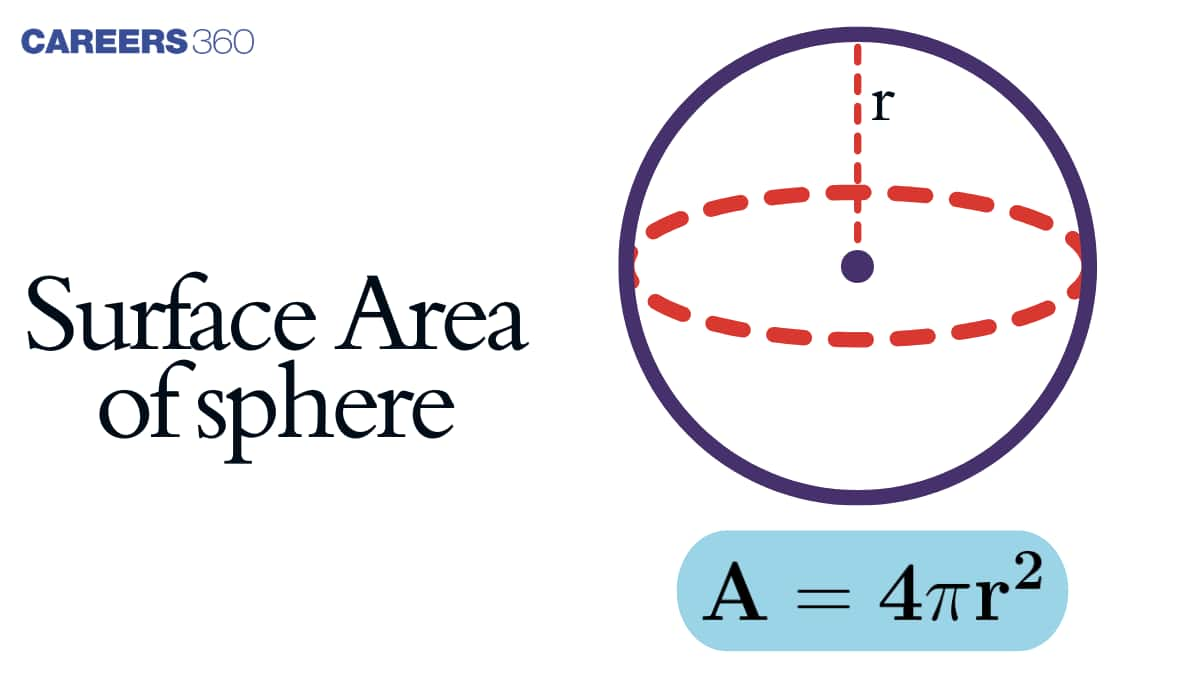
Surface Area of Sphere
Sphere can be defined as a 3-dimensional figure that has no edges or corners, has a smooth surface throughout and an axis of rotation which can be seen as its central point or axis. If we try to look on it from our mind, we can observe a disc like structure that we try to rotate it around its axis or diameter. The process of rotation that hence makes an image of a moving disc continuously in our mind can be termed as a sphere.
If we wish to paint a spherical ball that could be for a project or craft, or our football for a tournament, we have to know about the area of sphere to estimate the cost of paint that we would have to pay. Hence, we need to calculate the area or surface area of sphere. It is also known as total surface area of sphere, or curved surface area of sphere. All the surface areas of a sphere are just the same due to no difference in its configuration.

For any three-dimensional shapes, the area of the object can be categorised into three types. They are:
- Curved Surface Area
- Lateral Surface Area
- Total Surface Area
What is the curved surface area of sphere?
Curved Surface Area: It is the area of all the curved regions of the solid.
Lateral Surface Area: It is the area of all the regions except bases (i.e., top and bottom).
What is the total surface area of sphere?
Total Surface Area: It includes area of all the sides, top and bottom the solid object.
The curved surface area of sphere is the total surface area of sphere as it has just one surface which is curved. Since there is no flat surface in a sphere, the lateral surface are and the curved surface area of sphere is equal to the total surface area of sphere.
Surface Area of Sphere Formula
The formula for surface area of sphere in terms of $\mathrm{pi}(\pi)$ is given by:
Surface area of Sphere Formula $=4 \pi r^2$ square units
Derivation of Surface Area of Sphere
We take the help of cylinder to derive curved or lateral surface area of sphere. Defining a cylinder, we can say that a cylinder is a shape that has a curved surface along with flat surfaces. We assume that the radius of a cylinder is the same as the radius of a sphere. This means that height of both figures are equal. So, we take this height to be diameter of sphere. Hence, the fact was proved by great mathematician, Archimedes, that if the radius of a cylinder and sphere is 'r', the surface area of sphere is equal to the lateral surface area of cylinder.
Curved or Total Surface Area of Sphere = Lateral Surface Area of Cylinder
The lateral surface area of a cylinder $=2 \pi r$.
We can also say that height of the cylinder $=$ diameter of sphere $=2 \mathrm{r}$., since the sphere fits into the cylinder perfectly.
So, in the formula, surface area of Sphere $=2 \pi r h$; 'h' can be replaced by the diameter, 2 r . Hence, surface area of sphere formula $=2 \pi r h=2 \pi r(2 r)=4 \pi r^2$
Total Surface Area of Sphere Formula
Formula for Surface Area of Sphere is given by,
$A=4 \pi r^2$ square units
Curved Surface Area of Sphere Formula
Formula for surface area of sphere or the Formula for curved surface area of sphere is expressed as, CSA of sphere = $4 \pi r^2$; where $r=$ radius
Volume of Sphere
The volume area of sphere is defined as the number of cubic units needed to fill a sphere. So, we can say that it is the total volume that can be contained by the sphere.
The formula for volume of sphere is given by:
Volume $=\frac{4}{3} \pi r^3$ (Cubic Units)
Solved Examples
Example 1: What is the surface area of sphere whose radius is 10 ft ? (Use $\pi=3.14$ ).
Solution: Given, the radius 'r' of the sphere $=10$ feet.
Formula of surface area of sphere $=4 \pi r^2=4 \times \pi \times 10^2=1256$ feet $^2$
$\therefore$ The area of sphere is 1256 feet $^2$
Example 2: What is the curved surface area of sphere if its radius is given as 2 units.
Solution: Given, the radius $=2$ units.
$\Rightarrow$ Formula of area of sphere $=4 \pi r^2=4 \times \pi \times 2^2=4 \times 3.14 \times 4=20.24$ unit $^2$
$\therefore$ The surface area of sphere is 20.24 unit $^2$
Example 3: Find the surface area of sphere of diameter 21 cm .
Solution: $R=\frac{21}{2}=10.5 \mathrm{~cm}$
Formula of area of sphere $=4 \pi r^2$
$
=4 \times 3.14 \times 10.5 \times 10.5=1384.74 \mathrm{~cm} \mathrm{sq}
$
Example 4: Find the volume of a sphere of diameter 10 m , rounding your answer to two decimal places(using pi $=3.14$ ).
Solution: Diameter of the sphere $(\mathrm{d})=10 \mathrm{~m}$
Radius of the sphere $(\mathrm{r})=\frac{\mathrm{d}}{2}=\frac{12}{2}=5 \mathrm{~m}$
Volume of the sphere $(V)= \frac{4}{3} \pi r^3$
$
\begin{aligned}
& V=\frac{4}{3} \times 3.14 \times 5^3 \\
& V=\frac{4}{3} \times 3.14 \times 5 \times 5 \times 5 \\
& V=523.33 \mathrm{~m}^3
\end{aligned}
$
Example 5: A plane passes through the centre of a sphere and forms a circle with a radius of 14 feet. What is the total surface area of sphere?
Solution: Radius of the sphere $=14$ feet
Volume of the sphere $(V)=4 \pi r 3$
$
\begin{aligned}
& =4 \times 3.14 \times 14 \times 14 \times 14 \\
& =34,464.64 \text { feet }^2
\end{aligned}
$
List of Topics Related to Area of Sphere
| Area of Circle | Area of Isosceles Triangle |
| Area of Rectangle | Area of Square |
| Area | Area of Quadrilateral |
| Area of Parallelogram | Area and Perimeter |
| Area of Equilateral Triangle | cm to inches converter |
Frequently Asked Questions (FAQs)
The surface area of sphere is defined as the region occupied by its surface in a 3-D space. Surface area of Sphere Formula $=4 \pi r^2$ square units
The formula to find the surface area of sphere is 4 times of $\mathrm{pi}(\pi)$ and radiussquared $\left(r^2\right)$.
Surface area of sphere $=4 \pi r^2$
It is same as that of area of sphere. The area of sphere is defined as the region occupied by its surface in a 3-D space. Area of Sphere=4 \pi r^2$ square units.
If radius $=2 \mathrm{~cm}$
Area of sphere $=4 \pi r^2=4 \pi(2)^2$
$
=16 \pi \mathrm{sq} . \mathrm{cm} .
$
The distance from the centre to the outermost surface is called the radius of the sphere.