Area of Square Formula and Solved Examples

Edited By Team Careers360 | Updated on Jul 02, 2025 05:13 PM IST

A square is a closed two-dimensional shape with four equal sides and angles. The four sides form the four angles at the vertices or corners of the figure. Squares are most commonly found in our surroundings in the form of carromboard, chessboards, a side of dice etc. We know that the area is in general the space or the region covered by the object. While calculating the area of square, we have to observe only the length of its side. Since we are aware of the result that all sides of a square are equal, hence, area of square is equal to the square of the side of the square.

This Story also Contains

What is the Area of Square?
How to Find Area of Square?
Area of square formula example
Area of a Square Sample Problems

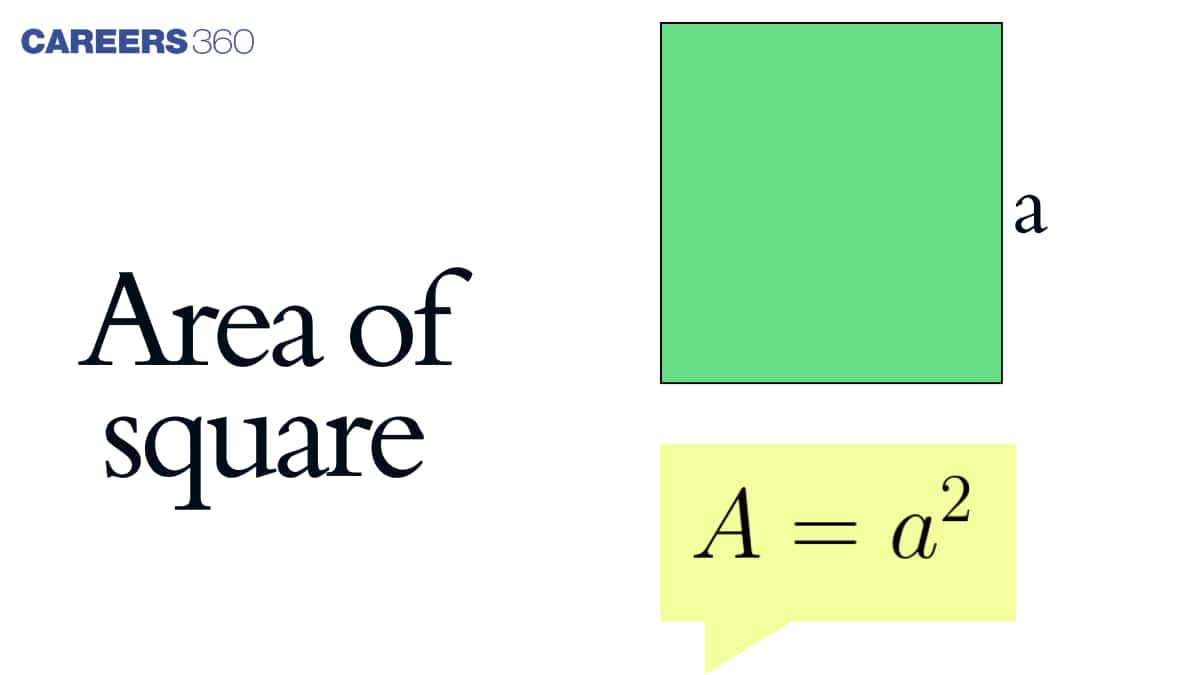
Area of Square Formula and Solved Examples

In this article we will discuss about what is the area of square, how to find area of square using diagonal, etc and also understand the concept in detail.

What is the Area of Square?

A square is a 2 dimensional shape with four equal sides and four vertices. Squares can be found all around us in the form of chessboard, the clock, and a blackboard, etc. When we talk about perimeter and area of square, perimeter is found by taking the sum of all sides and area of square by squaring the measure of one side. Area of square is defined as the space coveredd by square in a 2D space or the xy plane. Now let us look into area of square formula.

Formula of area of square is defined as the product of the length of two of its sides. It is always measured in square units. Hence, Formula of area of square = Side × Side = ${S}^2$. The common units of the area of square are $\mathrm{m}^2$, inches ${ }^2, \mathrm{~cm}^2$, and $\mathrm{ft}^2$.

What is the formula of area of square?

From the above discussion, we now know that we can define the area of square as the product of the length of its sides.

Formula for area of square = $s \times s={s}^2$

where $s$ is the square side.

Area of square using the length of the diagonal:

From the following figure, '$d$' is the diagonal and '$s$' represents the sides of the square.

Here the side of the square is ' $s$ ' and the diagonal of the square is ' $d$ '. We apply Pythagoras theorem,

$d^2=s^2+s^2$

$d^2=2 s^2$

$d=\sqrt{ 2s}$

$s=\frac{d}{\sqrt{2 }} $.

Now, using the diagonal, Formula for area of square $=s^2=(\frac{d}{\sqrt{2 }})^2=\frac{d^2}{2}$. Hence, the area of square formula $=\frac{d^2}{2}$.

Surface Area of Square

Surface area of square is a measure of space or the area covered by square. The formula of area of square is applicable here. In other words, surface area of square is equal to the area of square. We can say that both terms refer to the area of square only. The unit is always in square units.

How to Find Area of Square?

We can find area of square depending on what values are given to us and what is missing. The values here include the sides of square or the diagonal. Some values might be given to us while some might be missing. So, let us see some situations when the perimeter of a square is given, when the sides of square are given, or when the diagonal is given.

Area of square formula example

Now let us look into some area of square formula examples.

Area of Square when the Perimeter of Square is Given

Example: Find the area of square park whose perimeter is 300 ft .
Solution:
Given: Perimeter of square park $=300 \mathrm{ft}$
We know that,
Perimeter of square $=4 \times$ side

$
\begin{aligned}
& \Rightarrow 4 \times \text { side }=300 \\
& \Rightarrow \text { side }=\frac{300}{4}\\
& \Rightarrow \text { side }=75 \mathrm{ft}
\end{aligned}
$

Area of square is equal to $ side^2$
Hence, Area of park $=75^2=75 \times 75=5625 \mathrm{ft}^2$
Thus, the area of square park whose perimeter is 300 ft is $5625 \mathrm{ft}^2$

Area of Square When the Side of Square is Given

Example: Find the area of square whose side is 2 cm.
Solution:
Given: Side of square $=2 \mathrm{~cm}$
We know that,
Area of square is equal to $ side^2$
Hence, the area of square $=2^2=2 \times 2=4 \mathrm{~cm}^2$

Area of Square using Diagonal

Example: Find the area of square using diagonal as 10 cm.
Solution:
Given: Diagonal of square $=10 \mathrm{~cm}$
We know that,
Area of square using diagonal $=\frac{d^2}{2}$
Hence, the area of square $=\frac{(10 \times 10)}{2}=50 \mathrm{~cm}^2$

Area of a Square Sample Problems

Example 1: Find the area of square clipboard whose side measures 12 cm .
Solution:
Side of the clipboard that is in shape of square $=12 \mathrm{~cm}$
Hence, Area of square is equal to area of clipboard$=$ side $\times$ side

$
\begin{aligned}
& =12 \mathrm{~cm} \times 12 \mathrm{~cm} \\
& =144 \mathrm{sq} \cdot \mathrm{~cm}
\end{aligned}
$

Example 2: The side of square wall is 70 m. What is the cost of painting it at the rate of Rs. 3 per sq. m?

Solution:
Side of the wall $=70 \mathrm{~m}$
Area of square wall $=$ side $\times$ side $=70 \mathrm{~m} \times 70 \mathrm{~m}=4900 \mathrm{sq} . \mathrm{m}$
For 1 sq. m, the cost of painting = Rs. 3
Thus, for 5,625 sq. $m$, the cost of painting $=$ Rs. $3 \times 4900=$ Rs 14700 .

Example 3: A courtyard's floor which is 20 m long and 10 m wide is to be covered by square tiles. The side of each tile is 2 m. Find the number of tiles required to cover the floor.

Solution:
Length of the floor $=20 \mathrm{~m}$
The breadth of the floor $=10 \mathrm{~m}$
Area of floor $=$ length $\times$ breadth $=20 \mathrm{~m} \times 10 \mathrm{~m}=200 \mathrm{sq} . \mathrm{m}$
Side of square tile $=2 \mathrm{~m}$
Area of square tile $=$ side $\times$ side $=2 \mathrm{~m} \times 2 \mathrm{~m}=4 \mathrm{sq} \cdot \mathrm{m}$
No. of tiles required $= \frac{\text{ area of floor}}{\text{area of square tile}} =\frac{200}{4}=50$ tiles.

Example 4: The area of a square-shaped carrom board is $360 \mathrm{~cm}^2$. What is the length of its side?
Solution:
Area of the square carrom board $=360 \mathrm{~cm}^2$.

We know that Area of square$=$ side $\times$ side $= side^2$.
So, side $=\sqrt{ Area}$ $=\sqrt{360}=18.9 \mathrm{~cm}$.

Therefore, the side of the carrom board is 18.9 cm.

Example 5: What is area of square whose diagonal is 6 feet?
Solution:
The area of square when its diagonal is given is,

Formula for area of square $= \frac{\text{Diagonal }^2}{ 2}$.

Given, diagonal $(\mathrm{d})=6 \mathrm{ft}$.

Hence, area of square using diagonal $=\frac{(6 \times 6) }{2}=\frac{36}{ 2}=18$ square feet.

Therefore, the area of square is equal to 18 square feet.

List of Topics Related to Area of Square

Area of Circle	Area of Isosceles Triangle
Area of Rectangle	Area of Sphere
Area	Area of Quadrilateral
Area of Parallelogram	Area and Perimeter
Area of Equilateral Triangle	cm to inches converter

Frequently Asked Questions (FAQs)

1. Define area of square.

Area of square is defined as the number of square units that make a complete square. It is calculated by using the area of square formula: Formula of area of square $=$ side $\times$ side.

2. What is the formula of area of square?

Area of square with side 'a': Area $=a \times a=s^2$. However, area of square using diagonal, formula used to find the area of square is, $=\frac{\mathrm{d}^2 }{2}$.

3. How do we find area of square?

The Area of square is calculated with the help of the formula: Area of square is equal to $s^{\wedge} 2$, where, 's' is one side of the square. Since the area of square is a 2-D quantity, it is always expressed in square units.

4. What is perimeter and area of square?

The perimeter of square is a sum of the four sides of a square that is Perimeter $=4 \times$ Side. Whereas, area of square is equal to $ Area $$=\mathrm{s} \times \mathrm{s}$, where, 's' is one side of the square.

5. What are the units of area of square?

The common units are $\mathrm{m}^2$, inches ${ }^2, \mathrm{~cm}^2$, and $\mathrm{ft}^2$.

6. How does the concept of a square unit relate to the idea of dimensional analysis?

Square units (like m²) represent two-dimensional measurements, reflecting that area is a product of two lengths. This is part of dimensional analysis, where the units of a quantity reflect its physical nature.

7. How does the concept of a square foot relate to the area formula of a square?

A square foot is a square with sides of 1 foot. It's a standard unit of area measurement. The area formula A = s² tells us that any square with side length s feet will contain s² square feet.

8. Can you use the area formula of a square to explain why multiplying two negative numbers gives a positive result?

Yes, this can be explained geometrically. A square with a negative side length, say -s, has an area of (-s)² = s². This is positive because area is always non-negative, showing why negative × negative = positive.

9. Can you use the area formula of a square to understand why (a+b)² ≠ a² + b²?

Yes, this can be visualized geometrically. (a+b)² represents the area of a square with side (a+b). This square includes not just squares of sides a and b, but also two rectangles of area ab. So (a+b)² = a² + 2ab + b².

10. How can you use the area formula of a square to understand the concept of square roots?

The square root of a number is the side length of a square with that number as its area. For example, √25 = 5 because a square with side 5 has area 25. This gives a geometric interpretation to square roots.

11. How does the area of a square change if you double its side length?

If you double the side length of a square, its area increases by a factor of four. This is because the area is proportional to the square of the side length. For example, if the original area was A = s², the new area would be A = (2s)² = 4s².

12. Can the area of a square ever be negative?

No, the area of a square can never be negative. Area is a measure of the space inside a shape, which is always positive or zero. Even if a side length is negative, when squared, it becomes positive.

13. How does the area of a square compare to the area of a rectangle with the same perimeter?

Among all rectangles with a given perimeter, the square has the largest area. This is known as the isoperimetric property of squares. It demonstrates why squares are efficient shapes for enclosing space.

14. What happens to the area of a square if you increase its side length by 1 unit?

If you increase the side length by 1 unit, the new area will be (s+1)². This expands to s² + 2s + 1. The increase in area is 2s + 1 square units, which is more than just adding 1 to the original area.

15. How is the area of a square related to the area of a triangle with the same base and height?

The area of a square is exactly twice the area of a triangle with the same base and height. This is because a square can be divided into two equal right triangles by its diagonal.

16. How can you use algebra to prove the area formula for a square?

You can prove the formula by considering a square of side s and dividing it into s rows, each containing s unit squares. The total number of unit squares is s × s = s², which is the area.

17. Why is it incorrect to add the lengths of all sides to find the area of a square?

Adding the lengths of all sides gives the perimeter, not the area. Area is a measure of the space inside the square, which is proportional to the square of the side length, not its sum.

18. How does the concept of a square relate to perfect square numbers?

Perfect square numbers are the areas of squares with integer side lengths. For example, 16 is a perfect square because it's the area of a square with side length 4. This connects geometry to number theory.

19. How can you use the area formula of a square to explain why √2 is irrational?

If √2 were rational, it could be expressed as a/b where a and b are integers with no common factors. But (a/b)² = 2 implies a² = 2b². This is impossible for integers, proving √2 is irrational.

20. Why is the area of a square not directly proportional to its side length?

The area is not directly proportional to side length because it increases with the square of the side length. If you double the side length, the area quadruples, not doubles, showing a quadratic rather than linear relationship.

21. Why does squaring the side length give us the area of a square?

Squaring the side length gives us the area because a square has equal sides and right angles. When we multiply the length by the width, we're essentially counting the number of unit squares that fit inside the larger square.

22. What's the difference between perimeter and area of a square?

Perimeter is the distance around the square (the sum of all side lengths), while area is the space inside the square. For a square, perimeter is 4s, where s is the side length, and area is s².

23. If you know the area of a square, how can you find its side length?

To find the side length of a square when given its area, you need to take the square root of the area. If A is the area, then the side length s = √A.

24. Why is the unit for area squared (e.g., cm², m²) while length is not?

Area is measured in squared units because it represents a two-dimensional space. It's the product of two lengths (length and width), so we multiply the units as well. For example, 3 cm × 3 cm = 9 cm².

25. Can two squares with different side lengths have the same area?

No, two squares with different side lengths cannot have the same area. The area of a square is uniquely determined by its side length, and there's a one-to-one correspondence between side length and area.

26. How does the area of a square change if you rotate it?

The area of a square doesn't change when you rotate it. Rotation changes the square's orientation but not its size or shape, so the area remains constant.

27. What's the difference between linear and square units in the context of a square's measurements?

Linear units (like cm or m) are used for measuring the side length of a square, while square units (cm² or m²) are used for measuring its area. The square units are the product of two linear units.

28. If you cut a square in half diagonally, what fraction of the original area does each triangle represent?

Each triangle represents exactly half of the square's area. This is because the diagonal of a square creates two congruent right triangles, each with base and height equal to the square's side length.

29. How does the area of a square compare to the area of its inscribed circle?

The area of an inscribed circle is π/4 times the area of the square. This is because the diameter of the circle equals the side of the square, so if the square has side s, the circle has radius s/2.

30. Can you have a square with an area of 3 square units?

Yes, you can have a square with an area of 3 square units, but its side length would be √3, which is an irrational number. This square couldn't be constructed exactly with rational measurements.

31. How does the concept of square units relate to the area formula of a square?

Square units are the standard way to measure area. When we calculate s², we're essentially finding how many unit squares (squares with side length 1) can fit inside the larger square. This directly relates to the definition of area.

32. What is the formula for the area of a square?

The area of a square is calculated by multiplying the length of one side by itself. The formula is A = s², where A is the area and s is the length of a side.

33. Why doesn't doubling the area of a square double its side length?

Doubling the area doesn't double the side length because of the square relationship. To double the area, you need to multiply the side length by √2, not 2. This is because (s√2)² = 2s².

34. How does the area of a square relate to its scale factor?

If you scale a square by a factor k, its area is scaled by a factor of k². For example, if you double the side length (k=2), the area becomes 4 times larger.

35. Can the area of a square be expressed as a fraction?

Yes, the area of a square can be expressed as a fraction. If the side length is a fraction, like 3/4, the area would be (3/4)² = 9/16 square units.

36. What's the relationship between the area of a square and the area of a circle inscribed within it?

The area of a circle inscribed in a square is π/4 times the area of the square. This relationship comes from the fact that the diameter of the circle equals the side length of the square.

37. If you know the diagonal of a square, how can you find its area?

If d is the diagonal of a square, you can find its area using the formula A = d²/2. This is because the diagonal of a square forms two equal right triangles, and the Pythagorean theorem relates the diagonal to the side length.

38. How does the area of a square change if you triple its side length?

If you triple the side length, the area increases by a factor of nine. This is because (3s)² = 9s². It demonstrates how small changes in side length can lead to large changes in area.

39. How can you use the area formula of a square to find the side length of a square with area 100 cm²?

To find the side length, take the square root of the area. In this case, √100 cm² = 10 cm. This demonstrates how to reverse the area formula when the area is known.

40. If you increase the side length of a square by 10%, by what percentage does its area increase?

If you increase the side length by 10%, the new side length is 1.1s. The new area is (1.1s)² = 1.21s², which is a 21% increase. This shows that percentage increases in area are larger than those in side length.

41. If you know the perimeter of a square, how can you find its area?

If P is the perimeter of a square, each side has length P/4. The area is then A = (P/4)². This shows how perimeter and area are related, but not linearly.

42. How does the area of a square change if you construct another square on each of its sides?

If you construct squares on each side of the original square, the total area of the new shape will be 5 times the area of the original square. This relates to the concept of dissection puzzles and area addition.

43. If you have a square sheet of paper and fold it exactly in half, what happens to its area?

When you fold a square sheet exactly in half, its area is reduced by half. This is true regardless of how you fold it (diagonally or parallel to a side), demonstrating the additive property of area.

44. How does the area of a square relate to the concept of geometric sequences?

If you create a sequence of squares where each new square has a side length k times the previous one, the areas will form a geometric sequence with common ratio k². This connects area to exponential growth.

45. Can the area of a square ever equal its perimeter?

Yes, a square can have an area equal to its perimeter. This occurs when the side length is 4 units. In this case, both the area and perimeter equal 16 units².

46. How does the concept of a square relate to the Pythagorean theorem?

The Pythagorean theorem states that in a right triangle, a² + b² = c², where c is the hypotenuse. This can be visualized using squares: the sum of the areas of squares on the two shorter sides equals the area of the square on the hypotenuse.

47. If you inscribe a square inside a circle, what is the relationship between their areas?

The area of a square inscribed in a circle is half the area of the circle. If r is the radius of the circle, the side of the inscribed square is r√2, so its area is 2r², which is half of πr².

48. How can you use the area formula of a square to understand the concept of irrational numbers?

Irrational numbers often arise as side lengths of squares with rational areas. For example, a square with area 2 has side length √2, which is irrational. This shows how geometry can lead to the discovery of new number types.

49. If you have two squares, one with twice the side length of the other, how do their areas compare?

The square with twice the side length will have four times the area of the smaller square. This is because (2s)² = 4s², demonstrating the quadratic relationship between side length and area.

50. How does the area of a square change if you scale it in only one dimension?

If you scale a square in only one dimension, it becomes a rectangle. The area increases linearly with this scaling. For example, doubling one side doubles the area, unlike scaling both sides which would quadruple it.

51. If you know the area of a square in one unit system, how can you convert it to another?

To convert the area, you need to square the conversion factor between the linear units. For example, to convert from square feet to square meters, you'd multiply by (0.3048)², not just 0.3048.

52. How does the area of a square change if you cut off its corners to form an octagon?

The area decreases, but by how much depends on how much you cut off. If you cut triangles with side length x from each corner, the new area is s² - 4(x²/2) = s² - 2x², where s is the original side length.

53. How does the area of a square relate to the concept of integration in calculus?

The area of a square can be thought of as the integral of a constant function over a square region. This connects the simple area formula to more complex ideas in calculus about accumulating infinitesimal pieces.

54. If you have a square grid, how does the number of unit squares relate to the side length of the entire grid?

In a square grid, the number of unit squares is equal to the square of the number of units on each side. This directly relates to the area formula: if there are n units on each side, there are n² unit squares in total.

55. How can you use the area formula of a square to understand the concept of dimensional homogeneity in physics equations?

The area formula A = s² demonstrates dimensional homogeneity: the left side (area) has units of length squared, matching the right side (length squared). This principle is crucial in physics for ensuring equations are meaningful.