Argument of Complex Numbers - Definition, Formula, Example

The argument is related to the angle which is formed by complex numbers at the origin in the argand plane. There can be multiple arguments that exist for a single complex number but the principle argument is the only one. The applications of the arguments of complex numbers are in the phasor analysis, stability analysis of the control systems, signal processing, and analysis of wave function.

This Story also Contains

1. What are Complex Numbers?
2. Argument of Complex Numbers Definition
3. Argument of Complex Numbers Formula
4. How to Find the Argument of Complex Numbers?
5. Argument of a complex number in different quadrants
6. Properties of Argument of Complex Numbers
7. Applications Of Argument Of Complex Number

In this article, we will cover the concept of arguments of a complex number. This concept falls under the broader category of complex numbers. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of six questions have been asked on this concept, including one in 2013, one in 2019, one in 2020, one in 2022, and two in 2023.

What are Complex Numbers?

The number which has no real meaning then these numbers are represented in complex forms. The general form of complex numbers are $a+i b$ where i is iota or$\sqrt{-1}$.

For example,$z=5+2$ is a complex number.

5 here is called the real part and is denoted by Re(z), and 2 is called the imaginary part and is denoted by Im(z)

Argument of Complex Numbers Definition

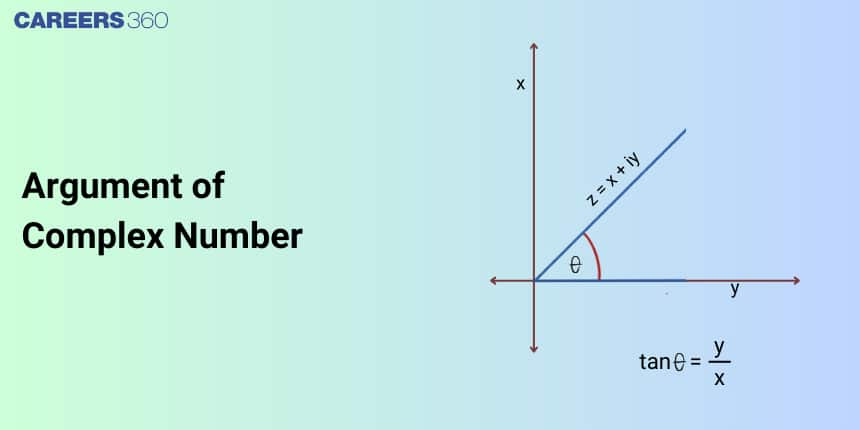
The argument of a complex number is the angle made by the line representation of the complex number, with the positive x-axis of the argand plane. Any complex number can be represented in the argand plane with the real part marked along the x-axis and the imaginary part marked along the y-axis. The complex number$Z=x+i y$ can be represented as a point $P(x, y)$in the argand plane, and the angle made by the line OP with the positive x-ais is the argument of the complex number.

Argument of Complex Numbers Formula

If a complex number $z=x+i y$ is represented by a point $P$ in the Argand plane and $O P$ forms some angle with a positive x-axis, let's denote it with $\theta$, then $\theta$ is called the argument of z.

$\begin{aligned} & \tan \theta=\frac{\mathrm{PM}}{\mathrm{OM}} \\ & \tan \theta=\frac{\mathrm{y}}{\mathrm{x}}=\frac{\operatorname{Im}(\mathrm{z})}{\operatorname{Re}(\mathrm{z})} \Rightarrow \theta=\tan ^{-1} \frac{\mathrm{y}}{\mathrm{x}} \\ & \arg (\mathrm{z})=\theta=\tan ^{-1} \frac{\mathrm{y}}{\mathrm{x}}\end{aligned}$

Principle Argument Of Complex Number = -π < θ < π

The principle argument of complex numbers has values from $-\pi<\theta<\pi$. Further, It is $0<\theta<\pi$, if taken in the first two quadrants where the angle is measured with respect to the positive $x$-axis in the anticlockwise direction. And it is $-\pi<\theta<0$ in the third and fourth quadrant, with respect to the positive $x$ axis, where the angle is measured along the clockwise direction. Further, the general argument of the complex number is $2 n \pi+\theta$.

General Argument Of Complex Number = 2nπ + θ

Thus the argument of the complex number is based on the trigonometric function, and hence it has the principle and general argument.

How to Find the Argument of Complex Numbers?

1. Find the real and imaginary parts from the given complex number. Denote them as x and y respectively.
2. Substitute the values in the formula θ = tan^-1 (y/x)
3. Find the value of θ if the formula gives any standard value, otherwise write it in the form of tan^-1 itself.
4. This value followed by the unit “radian” is the required value of complex argument for the given complex number.

Argument of a complex number in different quadrants

If $\theta$ lies between $-\pi<\theta \leq \pi$, then $\theta$ is called a principal argument. The value of the argument differs depending on which quadrant point $(x, y)$ lies.

If it lies in $1^{\text {st }}$ quadrant then it is $\theta$ (acute angle)

If the point lies in 2^nd quadrant, then $\arg (z)=\theta=\pi-\tan ^{-1} \frac{y}{|x|}$

So it will be an obtuse +ve angle

If the point lies in lies in 3^rd quadrant then $\arg (z)=\theta=-\pi+\tan ^{-1} \frac{y}{z}$

It will be an obtuse -ve angle

If the point lies in 4^th quadrant then $\arg (z)=\theta=-\tan ^{-1} \frac{|y|}{x}$

It will be -ve acute angle

Note:

If $\arg (\mathrm{z})=\frac{\pi}{2}$ or $-\frac{\pi}{2}, \mathrm{z}$ is purely imaginary.
If $\arg (\mathrm{z})=0$ or $\pi, \mathrm{z}$ is purely real.

Properties of Argument of Complex Numbers

i) $\arg \left(\mathrm{z}_1 \mathrm{z}_2\right)=\arg \left(\mathrm{z}_1\right)+\arg \left(\mathrm{z}_2\right)+2 \mathrm{k} \pi, \mathrm{k}$ is an integer

This formula for argument can be generalized for n number of complexes in a similar way

ii) $\arg \left(\frac{\mathrm{z}_1}{\mathrm{z}_2}\right)=\arg \left(\mathrm{z}_1\right)-\arg \left(\mathrm{z}_2\right)+2 \mathrm{k} \pi$ where k is an integer

$
\text { iii) } \arg (\bar{z})=-\arg (z)
$

iv) $\arg \left(\mathrm{z}^{\mathrm{n}}\right)=\mathrm{n} \cdot \arg (\mathrm{z})+2 \mathrm{k} \pi$ k belongs to an integer

(v) $\left|z_1+z_2\right|=\left|z_1\right|+\left|z_2\right| \Rightarrow \arg \left(z_1\right)=\arg \left(z_2\right)$
(vi) $\left|\mathrm{z}_1+\mathrm{z}_2\right|=|| \mathrm{z}_1|-| \mathrm{z}_2|| \Rightarrow \arg \left(\mathrm{z}_1\right)-\arg \left(\mathrm{z}_2\right)=\pi$

Applications Of Argument Of Complex Number

The argument of a complex number has numerous applications in transforming the complex number to polar form, and also in finding the relationship between the real part and the imaginary part of the complex number.

Polar Form of Complex Number: The polar form of the complex number is P = r(Cosθ + iSinθ). Here θ is the argument of the complex number, and r is the argument of the complex number. Polar form is another important form of representing the complex number in the argand plane. The polar form of the complex number represented in cartesian form is (rCosθ, rSinθ).

Summary

The arguments help in finding the position of the complex numbers in the argand plane. It provides extra knowledge about complex numbers and its applications are widely used in the analysis of phasor and control systems. Understanding the concept of the arguments is very essential for working with complex numbers in polar coordinates for various applications in science and engineering.

Solved Examples Based on Argument of a Complex Number

Example 1: Arg $\left(\frac{2 i}{\sqrt{3}-i}\right)$ equals:

Solution:

As we learned in

Definition of Argument/Amplitude of z in Complex Numbers -

$\theta=\tan ^{-1}\left|\frac{y}{x}\right|, z \neq 0$

$\theta, \pi-\theta,-\pi+\theta,-\theta$ are Principal Arguments if z lies in the first, second, third, or fourth quadrant respectively.

Now,

$\begin{aligned} & \frac{2 i}{\sqrt{3}-i}=\frac{2 i}{\sqrt{3}-i} \times \frac{\sqrt{3}+i}{\sqrt{3}+i}=\frac{2 \sqrt{3} i-2}{4} \\ & \Rightarrow \frac{2 i}{\sqrt{3}-i}=\frac{-1}{2}+\frac{i \sqrt{3}}{2}\end{aligned}$

$\because$ it lies in 2nd quadrant so

argument= $\pi-\tan ^{-1}\left|\frac{\frac{\sqrt{3}}{2}}{\frac{-1}{2}}\right|=\pi-\frac{\pi}{3}=\frac{2 \pi}{3}$

Hence, the required answer is $\frac{2 \pi}{3}$.

Example 2: Let $z_0$ be a root of the quadratic equation, $x^2+x+1=0$. If $z=3+6 i z_0^{81}-3 i z_0^{93}$ then arg z is equal to :

Solution:

Definition of Argument/Amplitude of z in Complex Numbers -

$\theta=\tan ^{-1}\left|\frac{y}{x}\right|, z \neq 0$

$\theta, \pi-\theta,-\pi+\theta,-\theta$ are Principal Arguments if z lies in the first, second, third, or fourth quadrant respectively.

now,

Cube roots of unity -

$z=(1)^{\frac{1}{3}} \Rightarrow z=\cos \frac{2 k \pi}{3}+i \sin \frac{2 k \pi}{3}$

k=0,1,2 so z gives three roots

$\Rightarrow 1, \frac{-1}{2}+i \frac{\sqrt{3}}{2}(\omega), \frac{-1}{2}-i \frac{\sqrt{3}}{2}\left(\omega^2\right)$

- wherein

$\omega=\frac{-1}{2}+\frac{i \sqrt{3}}{2}, \omega^2=\frac{-1}{2}-\frac{i \sqrt{3}}{2}, \omega^3=1,1+\omega+\omega^2=0$

$1, \omega, \omega^2$ are cube roots of unity.

Quadratic Equation

$x^2+x+1=0$, roots are, $\omega$ and $\omega^2$ where $\omega$ is the cube root of unity.

$
z=3+6 i\left(z_0\right)^{81}-3 i\left(z_0\right)^{90}
$

$z_0=\omega$ and $\omega^2$

$
\begin{aligned}
& z=3+6 i(\omega)^{81}-3 i(\omega)^{93} \\
& z=3+3 i \quad \because \omega^3=1 \\
& \arg (z)=\frac{1}{4}
\end{aligned}
$
Hence, the required answer is $\frac{\pi}{4}$.

Example 3: Which of the following is one of the arguments of $z=-\sqrt{3}-3 i$:

1) $\frac{\pi}{3}$
2) $\frac{-5 \pi}{3}$
3) $\frac{-4 \pi}{3}$
4) $\frac{4 \pi}{3}$

Solution

As we learned in

General Argument of a Complex Number -

$2 n \pi+0$

- wherein

$\theta$ is the principal argument of complex numbers.

$\because$ z lies in 3rd quadrant

$\therefore$ its principal argument $=-\pi+\tan ^{-1}\left|\frac{-3}{-\sqrt{3}}\right|=-\pi+\tan ^{-1} \sqrt{3}=-\pi+\frac{\pi}{3}=\frac{-2 \pi}{3}$

$\therefore 2 n \pi-\frac{2 \pi}{3}$ will be its general argument.

for n=1, we get argument = $\frac{4 \pi}{3}$

Hence, the required answer is the option (4).

Example 4: Let a complex number be $w=1-\sqrt{3} i$. Let the other complex number z be such that $|z w|=1$ and $\arg (z)-\arg (w)=\frac{\pi}{2}$. Then the area of the triangle with the vertices origin, a and w is equal to:

Solution:

$\begin{aligned} & \mathrm{w}=1-\sqrt{3} \cdot i \Rightarrow|\mathrm{w}|=2 \\ & \text { Now, }|\mathrm{z}|=\frac{1}{|\mathrm{w}|} \Rightarrow|\mathrm{z}|=\frac{1}{2} \\ & \text { and } \arg (\mathrm{z})=\frac{\pi}{2}+\arg (\mathrm{w})\end{aligned}$

Area of $\Delta=\frac{1}{2} \times 2 \times \frac{1}{2}=\frac{1}{2}$

Hence, the answer is $\frac{1}{2}$

Example 5: Arg $\left(i^{18}+\frac{1}{i^{25}}\right)$ equals:

Solution:

$i^{18}+\frac{1}{i^{25}}=\left(i^4\right)^4 \cdot i^2+\left(\frac{1}{i^4}\right)^6 \cdot \frac{1}{i}=i^2+\frac{1}{i}=-1-i$

As this lies in the third quadrant, so Arg(z) = $-\pi+\tan ^{-1} \left\lvert\, \frac{y}{x}\right.$

$\therefore$ Arg $(-1-i)=-\pi+\tan ^{-1}\left|\frac{-1}{-1}\right|=-\pi+\frac{\pi}{4}=\frac{-3 \pi}{4}$

Hence, the required answer is $\frac{-3 \pi}{4}$.