Complex number

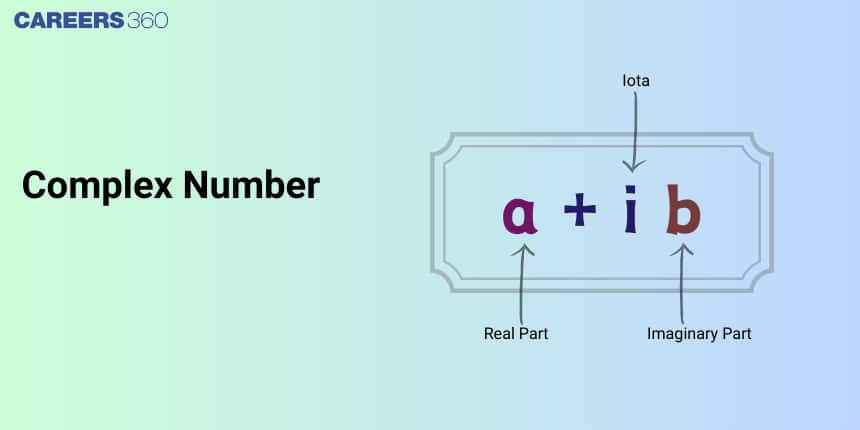
In mathematics, a complex number is a combination of real number and an imaginary part. It can be expressed as the form of $z=a+ib$, where $i$ is known as ‘iota’. Complex numbers are usually denoted by $z$.

In this article, we will discuss about the concepts of complex number. This category comes under “complex analysis” of mathematics. It is a crucial topic for the syllabus of class 11th mathematics. It is important for both boards and competitive exams such as JEE Main, SRMJEE, etc. A total of 11 questions have been asked from “complex numbers” in the last 10 years.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Complex Numbers
2. Types of a complex number
3. Graphical Representation
4. Argument of complex number
5. Absolute Value
6. Different Forms of Complex Numbers
7. Algebraic Operations on Complex Number
8. Roots of Complex Numbers
9. Complex Number Formulas
10. Power of Iota (i)
11. Identities
12. Properties
13. Importance of Complex Numbers
14. Solved Examples Based On Complex Numbers

Complex Numbers

A number which can be expressed in an expression form containing real and imaginary part. The general form of the complex number is written below:

$z=a+ib$, where

$i=\sqrt{-1}$

For example:
$z=4+3 i$
$z$ is a complex number.

Here, $4$ is called the real part and is denoted by $Re(z)$ and $3$ is the imaginary part and is denoted by $Im(z)$.

What are Real Numbers?

A number which can be represented on the number line, is the real number. It can be positive, negative, rational, irrational or zero. It is represented as $Re()$.

For example: $-4,1,0,\frac{3}{4},\sqrt{5}$, etc. are all real numbers.

Thus, real numbers broadly include all rational and irrational numbers. It is extended from negative infinity to positive infinity.

In interval form it is written as $R=(-\infty,\infty)$.

What are Imaginary Numbers?

The numbers which can not be represented on the number line are the imaginary numbers. Usually denoted by $Im()$. Contains $i$, where $i$ is iota.

For example: $\sqrt{-3 }-3, \sqrt{-5}, \sqrt{-1}$ are all imaginary numbers.

Types of a complex number

Purely Real and Purely Imaginary Complex Number

• A complex number is said to be purely real if its imaginary part is zero,

$\operatorname{Im}(z)=0$
$z=4+0 i \rightarrow z=4$

• A complex number is said to be purely imaginary if its real part is zero, $\operatorname{Re}(z)=0$
  $z=0+3 i \rightarrow z=3$

Note: All real numbers are also complex numbers (with $b=0$).

e.g. 5 can be written as $5+0 i$

So, $R$ is a proper subset of $C$, where $R$ is the set of real numbers and $C$ is the set of complex number..

Equality of Complex Numbers

The concept of equality of complex numbers is similar to the equality of real numbers.

Two complex numbers are said to be equal if and only if their corresponding real parts and their imaginary parts are equal.

$a+i b=c+i d$
$\Rightarrow \mathrm{a}=\mathrm{c}$ and $\mathrm{b}=\mathrm{d}$
$a, b, c, d \in R$ and $i=\sqrt{ }-1$

Also, the two complex numbers in the polar form are equal, if and only if they have the same magnitude and their argument (angle) differs by an integral multiple of $2π$.

Is $0$ a complex Number?

As we know, $0$ is a real number. And real numbers are part of complex numbers. Therefore, $0$ is also a complex number and can be represented as $0+0i$.

Graphical Representation

Argand Plane

The rectangular coordinate system on which a complex number is represented is known as the complex or Argand plane. It is similar to the Cartesian plane which is used for representing rea numbers.

In this $z = a + ib$ is represented by a point whose coordinates are $(a,b)$.

So, the $x$-coordinate of the point is the Real part of z, and the y-coordinate is the imaginary part of $z$

e.g. $z=-2+3 i$ is represented by the point $(-2,3)$ and it lies in the second quadrant.

Argument of complex number

The argument of a complex number tells us about the angle formed by the complex number on the argand plane with respect to positive real axis. For a complex number $z=a+ib$, the argument of $z$, is represented by:

$\theta=\arg (z)=\tan ^{-1}\left(\frac{y}{x}\right)$

Absolute Value

The absolute value of a real number is the number itself. The absolute value of $x$ is represented by modulus, i.e. $|x|$. Hence, the modulus of any value always gives a positive value, such that;

$|5| = 5$

$|-5| = 5$

Suppose, $z = x+iy$ is a complex number. Then, mod of $z$, will be:

$|z|=\sqrt{x^2+y^2}$

This expression is obtained when we apply the Pythagorean theorem in a complex plane. Hence, mod of complex number, $z$ is extended from $0$ to $z$ and mod of real numbers $x$ and y is extended from $0$ to $x$ and $0$ to $y$ respectively. Now these values form a right triangle, where $0$ is the vertex of the acute angle.

$ |z|^2 = |x|^2 + |y|^2 \\ |z|^2 = x^2 + y^2 \\ |z| = \sqrt{x^2 + y^2} $

Different Forms of Complex Numbers

There are various forms of complex numbers that are,

• Rectangular Form
• Polar Form
• Exponential Form

Rectangular Form

Also called Standard Form and it is represented by $(a + ib)$, where $a$ and $b$ are the real numbers.

For example: $(5 + 5i), (-7i), (-3 – 4i)$, etc.

Polar Form

It is the representation of a complex number where polar coordinates [where coordinates are represented as $(r, θ)$, where $r$ is the distance from the origin and $θ$ is the angle between the line joining the point and origin and the positive $x$-axis) are used to represent a complex number. Any complex number is represented as $r [cos θ + i sin θ]$.

For examples: $[cos \frac{\pi}{2} + i sin \frac{\pi}{2}], 5[cos \frac{\pi}{6} + i sin \frac{\pi}{6}]$, etc.

Exponential Form

It is the representation of complex numbers using Euler’s Formula and in this form the complex number is represented by $r e^{i \theta}$, where $r$ is the distance of a point from the origin and $θ$ is the angle between the positive $x$-axis and radius vector.

For examples: $\mathrm{e}^{\mathrm{i}(0)}, \mathrm{e}^{\mathrm{i}(\pi / 2)}, 5 . \mathrm{e}^{\mathrm{i}(\pi / 6)}$ etc.

Algebraic Operations on Complex Number

The four operations on the complex numbers include :

• Addition
• Subtraction
• Multiplication
• Division

Roots of Complex Numbers

When we solve a quadratic equation in the form of $a x^2+b x+c=0$, the roots of the equations can be determined in three forms;

• Two Distinct Real Roots
• Similar Root
• No Real roots (Complex Roots)

Complex Number Formulas

While performing the arithmetic operations of complex numbers such as addition and subtraction, combine similar terms. It means that combine the real number with the real number and imaginary number with the imaginary number.

Addition

(a + ib) + (c + id) = (a + c) + i(b + d)

Subtraction

(a + ib) – (c + id) = (a – c) + i(b – d)

Multiplication

When two complex numbers are multiplied by each other, the multiplication process should be similar to the multiplication of two binomials. It means that the FOIL method (Distributive multiplication process) is used.

(a + ib). (c + id) = (ac – bd) + i(ad + bc)

Division

The division of two complex numbers can be performed by multiplying the numerator and denominator by its conjugate value of the denominator, and then applying the FOIL Method.

$\frac{(a + ib) }{ (c + id)} = \frac{(ac+bd)}{(c^2+d^2)} + i\frac{(bc – ad)}{(c^2+d^2)}$

Power of Iota (i)

Depending upon the power of $“i”$, it can take the following values;

$i i^{4 k+1}=i . i^{4 k+2}=-1 i^{4 k+3}=-i . i^{4 k}=1$

Where $k$ can have an integral value (positive or negative).

Similarly, we can find for the negative power of $i$, which are as follows;

$\mathrm{i}^{-1} = \frac{1}{i}$

Identities

• $ (z_1 + z_2)^2 = z_1^2 + z_2^2 + 2 z_1 z_2 \\ (z_1 - z_2)^2 = z_1^2 + z_2^2 - 2 z_1 z_2 \\ z_1^2 - z_2^2 = (z_1 + z_2)(z_1 - z_2) \\ (z_1 + z_2)^3 = z_1^3 + 3z_1^2 z_2 + 3z_2^2 z_1 + z_2^3 \\ (z_1 - z_2)^3 = z_1^3 - 3z_1^2 z_2 + 3z_2^2 z_1 - z_2^3 $

Properties

The properties of complex numbers are listed below:

• The addition of two conjugate complex numbers will result in a real number
• The multiplication of two conjugate complex number will also result in a real number
• If $x$ and $y$ are the real numbers and $x+iy =0$, then $x =0$ and $y =0$.
• If $p, q, r$, and s are the real numbers and $p+qi = r+si$, then $p = r$, and $q=s$.
• The complex number holds the commutative law of addition and multiplication.

$ z_1 + z_2 = z_2 + z_1 \\ z_1 \cdot z_2 = z_2 \cdot z_1 $

• The complex number follows the associative law of addition and multiplication.

$ (z_1 + z_2) + z_3 = z_1 + (z_2 + z_3) \\ (z_1 \cdot z_2) \cdot z_3 = z_1 \cdot (z_2 \cdot z_3) $

• The complex number holds the distributive law

$ z_1 \cdot (z_2 + z_3) = z_1 \cdot z_2 + z_1 \cdot z_3 $

• For any two complex numbers, say z₁ and z₂, then $ |z_1 + z_2| \leq |z_1| + |z_2| $.

Importance of Complex Numbers

Complex numbers are important because they extend the real number system to include solutions to equations that have no real solutions.

• Solve Polynomial Equations: Some polynomial equations do not have real solutions. For example, the equation $x^2 + 1 = 0$ has no real solution because the square of any real number is non-negative. However, using complex numbers, the solutions are $x=i$ and $x=−i$.
• Completeness: The set of complex numbers is algebraically closed, meaning every non-constant polynomial equation with complex coefficients has a solution in the complex numbers.
• Simplify Calculations: In some cases, working with complex numbers can simplify mathematical expressions and calculations, especially in trigonometry and calculus.
• Applications in Various Fields: Complex numbers are used extensively in engineering, physics, computer science, and other fields.

Recommended Video Based on Complex Numbers

Solved Examples Based On Complex Numbers

Below are some examples based on the concept of complex number:

Example 1: Let $\alpha, \beta$ be real and $z$ be a complex number. If $z^2+\alpha z+\beta=0$ has two distinct roots on the line $\operatorname{Re} z=1$, then it is necessary that

Solution:

As we learned in

Definition of Complex Number -

$z=x+i y, x, y \in R \quad \& i^2=-1$

- where Real part of $z = Re (z) = x$ & Imaginary part of $z = Im (z) = y$

$z=x+i y, x, y \in R {\& i^2=-1}$
- where Real part of $z=\operatorname{Re}(z)=x$ \& Imaginary part of $z=\operatorname{Im}(z)=y$
$z^2+\alpha z+\beta=0$

Let $z=1+$ iy
$ \begin{aligned} & \text{So that } (1 + i y)^2 + \alpha(1 + i y) + \beta = 0 \\ & \Rightarrow \quad 1 - y^2 + i 2y + \alpha + i \alpha y + \beta = 0 \\ & \therefore \quad \left(1 - y^2 + \alpha + \beta\right) + i(2 + \alpha)y = 0 \\ & \therefore \quad \alpha = -2 \text{ and } 1 - y^2 - 2 + \beta = 0 \\ & \Rightarrow \quad y^2 = \beta - 1 > 0 \\ & \therefore \quad \beta - 1 > 0 \end{aligned} $ $ \beta \in (1, \infty) $

Hence, the answer is $\beta \in(1, \infty)$.

Example 2: The complex number having the sum of the real part and imaginary part 6 and the real part is also double of an imaginary part will be:

1) $8-21$
2) $4+21$
3) $3+32$
4) $5+7$

Solution

Let the complex number $x+i y$

where x will be the real part and y will be the imaginary part.

According to the given conditions

$ x + y = 6 $ \qquad $ x = 2y $

Solving (1) and (2) we get $\mathrm{x}=4$ and $\mathrm{y}=2$

So, the complex number will be $4+2 \mathrm{i}$ Hence, the answer is option (2).

Example 3: A complex number z is such that the sum of its real and imaginary parts is zero, if 5 is added to the imaginary part, then the imaginary part becomes 8, then z equals:

Solution:

As we learned in

Definition of Complex Number -

$z=x+i y, x, y \in R_{\&} \mathrm{i}^2=-1$
- wherein

Real part of $z=\operatorname{Re}(z)=x$ \& Imaginary part of $z=\operatorname{Im}(z)=y$
Let $z=x+i y$ then $\operatorname{Re}(z)=x$ and $\operatorname{Im}(z)=y$
According to the given conditions $\rightarrow$
$ x + y = 0 $ $ y + 5 = 8 $

From (1) and (2): $x=-3, y=3$
$\therefore z=-3+3 i$

Hence, the answer is $-3+3 i$.

Example 4: The complex number z is such that its real part is thrice the imaginary part, if both real and imaginary parts are increased by 1 then the real part becomes double of the imaginary part. Then z equals:

Solution:

As we learned in

Definition of Complex Number -

$ \begin{aligned} & z = x + i y, \quad x, y \in \mathbb{R} \quad \text{and} \quad i^2 = -1 \\ & \text{ - wherein} \end{aligned} $
- wherein

Real part of $z=\operatorname{Re}(z)=x$ \& Imaginary part of $z=\operatorname{Im}(z)=y$
Let $z=x+i y$ then according to the given conditions $\rightarrow$ x = 3y $ \qquad $ x + 1 = 2(y + 1) \Rightarrow x = 2y + 1 $

$\text{From (1) and (2) we get } x = 3 \text{ and } y = 1 $ $ \therefore z = 3 + i $

Hence, the answer is $3+\mathrm{i}$.

Example 5: A value of $\theta$ for which $\frac{2+3 i \sin \theta}{1-2 i \sin \theta}$ is purely imaginary is :

Solution:

As we learned in

Purely Real Complex Number -
$ z = x + i y, \quad x \in \mathbb{R}, \quad \mathbf{y} = \mathbf{0} $ \qquad $ i^2 = -1 $
wherein
Real part of $z=\operatorname{Re}(z)=x$ \& Imaginary part of $z=\operatorname{Im}(z)=y$
Let $Z=\frac{2+3 i \sin \theta}{1-2 i \sin \theta}$
$Z=\frac{2+3 i \sin \theta}{1-2 i \sin \theta} \times \frac{1+2 i \sin \theta}{1+2 i \sin \theta}$
$=\frac{(2+3 i \sin \theta)(1+2 i \sin \theta)}{1+4 \sin ^2 \theta}$
$=2-6 \sin ^2 \theta=0$ for purely imaginary, a real part must be zero.
$\sin ^2 \theta=\frac{2}{6}=\frac{1}{3}$
$\sin ^2 \theta=\frac{1}{\sqrt{3}}$
$\theta=\sin ^{-1} \frac{1}{\sqrt{3}}$

Hence, the answer is $\theta=\sin ^{-1} \frac{1}{\sqrt{3}}$.