Coplanarity of Two Lines in 3D Geometry

When there is more than one line and all lie on the same plane, we say that all lines are coplanar. We can also say two lines are said to be coplanar if both lie on the same plane. Coplanar lines are used in the fields of maths, physics, and engineering.

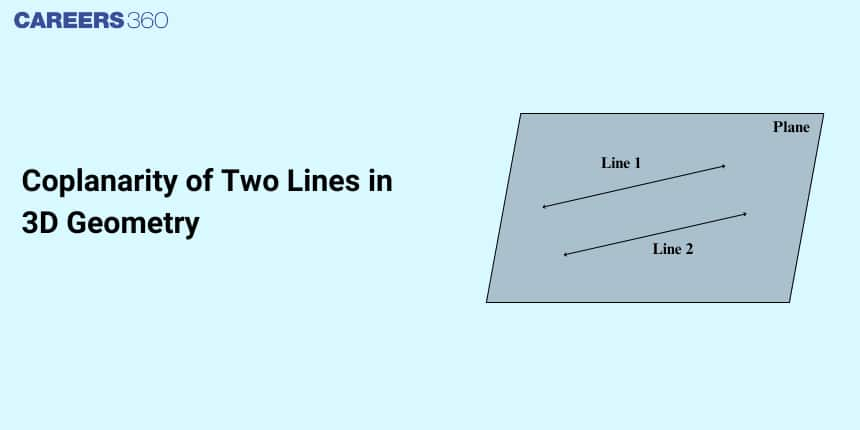
In this article, we will cover the concept of the Coplanarity of Two Lines. This topic falls under the broader category of Three Dimensional Geometry, which is a crucial chapter in Class 12 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of twelve questions have been asked on this topic in JEE Main from 2013 to 2023 including one in 2020, three in 2021, four in 2022, and three in 2023.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Coplanarity of Two Lines
2. Condition of Coplanarity in Cartesian Form
3. Condition of Coplanarity in Vector Form
4. How Can We Prove if Two Vectors Are Planar or Not?
5. Solved Examples Based on the Coplanarity of Two Lines

Coplanarity of Two Lines

Coplanarity refers to the property of lying within the same plane.

In a 3-dimensional space-

• Two lines are coplanar if there is a plane that includes them both. This is possible only if the lines are parallel or intersect.

• Three points are always coplanar, and if they are not collinear, the plane is unique.

• Four points may or may not lie in the same plane.

Equation of the Plane containing a Straight line

We studied in the previous concept that a line $\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$ to lie in the plane ax + by $+\mathrm{cz}+\mathrm{d}=0$ iff $a l+b m+c n=0$ and $a x_1+b y_1+c z_1+d=0$

Thus, the general equation of the plane containing a straight line

$
\begin{aligned}
& \frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n} \text { is } \\
& a\left(x-x_1\right)+b\left(y-y_1\right)+c\left(z-z_1\right)=0
\end{aligned}
$

where, $\quad a l+b m+c n=0$

The equation of the plane containing a straight line $\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$ and parallel to the straight line $\frac{x-x_2}{l_1}=\frac{y-y_2}{m_1}=\frac{z-z_2}{n_1}$

$
\left|\begin{array}{ccc}
x-x_1 & y-y_1 & z-z_1 \\
l & m & n \\
l_1 & m_1 & n_1
\end{array}\right|=0
$
Hence, the equation of the plane containing two given straight lines

$
\begin{aligned}
& \frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n} \\
& \text { and } \quad \frac{x-x_2}{l_1}=\frac{y-y_2}{m_1}=\frac{z-z_2}{n_1} \\
& \left|\begin{array}{ccc}
x-x_1 & y-y_1 & z-z_1 \\
l & m & n \\
l_1 & m_1 & n_1
\end{array}\right|=0 \\
& \text { or } \\
& \left|\begin{array}{ccc}
x-x_2 & y-y_2 & z-z_2 \\
l & m & n \\
l_1 & m_1 & n_1
\end{array}\right|=0
\end{aligned}
$

Condition of Coplanarity in Cartesian Form

The condition of coplanarity of the given straight lines is given by:

$$
\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
l & m & n \\
l_1 & m_1 & n_1
\end{array}\right|=0
$$

Condition of Coplanarity in Vector Form

If the line $\mathrm{E}_1: \overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_1+\lambda \overrightarrow{\mathbf{b}}_1$ and $\mathrm{Ł}_2: \overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_2+\lambda \overrightarrow{\mathbf{b}}_2$ are coplanar then,

$
\left[\begin{array}{lll}
\overrightarrow{\mathbf{r}}_1 & \overrightarrow{\mathbf{b}}_1 & \overrightarrow{\mathbf{b}}_2
\end{array}\right]=\left[\begin{array}{lll}
\overrightarrow{\mathbf{r}}_2 & \overrightarrow{\mathbf{b}}_1 & \overrightarrow{\mathbf{b}}_2
\end{array}\right]
$

and the equation of the plane containing them is

$
\begin{aligned}
& {\left[\begin{array}{lll}
\overrightarrow{\mathbf{r}} & \overrightarrow{\mathbf{b}}_1 & \overrightarrow{\mathbf{b}}_2
\end{array}\right]=\left[\begin{array}{lll}
\overrightarrow{\mathbf{r}}_1 & \overrightarrow{\mathbf{b}}_1 & \overrightarrow{\mathbf{b}}_2
\end{array}\right]} \\
& \text { or } \\
& {\left[\begin{array}{lll}
\overrightarrow{\mathbf{r}} & \overrightarrow{\mathbf{b}}_1 & \overrightarrow{\mathbf{b}}_2
\end{array}\right]=\left[\begin{array}{lll}
\overrightarrow{\mathbf{r}}_2 & \overrightarrow{\mathbf{b}}_1 & \overrightarrow{\mathbf{b}}_2
\end{array}\right]}
\end{aligned}
$

How Can We Prove if Two Vectors Are Planar or Not?

Two vectors can be planar or not.

The conditions are as follows:

1. If the given three vectors are linearly dependent on each other or not.

2. If the product of $3$ vectors is equal to zero.

3. ‘N’ vectors are coplanar if no more than two vectors are independent.

Recommended Video Based on Coplanarity of Two Lines

Solved Examples Based on the Coplanarity of Two Lines

Example 1: Let $\tilde{\mathrm{a}}, \tilde{\mathrm{b}}$ and $\tilde{\mathrm{c}}$ be three non-zero non-coplanar vectors. Let the position vectors of four points $A, B, C$ and $D_{\text {be }}$ $\vec{a}-\vec{b}+\vec{c}, \lambda \vec{a}-3 \vec{b}+4 \vec{c},-\vec{a}+2 \vec{b}-3 \vec{c}$ and $2 \vec{a}-4 \vec{b}+6 \vec{c}$ respectively. If $\overrightarrow{A B}, \overrightarrow{A C}$ and $\overrightarrow{A D}$ are coplanar, then $\lambda$ is equal to
[JEE MAINS 2023]

Solution

$
\begin{aligned}
\overrightarrow{\mathrm{AB}}= & (\lambda \overrightarrow{\mathrm{a}}-3 \vec{b}+4 \vec{c})-(\vec{a}-\vec{b}+\vec{c}) \\
& =(\lambda-1) \vec{a}-2 \vec{b}+3 \vec{c} \\
\overrightarrow{\mathrm{AC}}= & (-\vec{a}+2 \vec{b}-3 \vec{c})-(\vec{a}-\vec{b}+\vec{c}) \\
& =-2 \vec{a}+3 \vec{b}-4 \vec{c} \\
\overrightarrow{\mathrm{AD}}= & (2 \vec{a}-4 \vec{b}+6 \vec{c})-(\vec{a}-\vec{b}+\vec{c}) \\
& =\vec{a}-3 \vec{b}+5 \vec{c}
\end{aligned}
$
For coplanar vectors

$
\begin{aligned}
& \left|\begin{array}{ccc}
\lambda-1 & -2 & 3 \\
-2 & 3 & -4 \\
1 & -3 & 5
\end{array}\right|=0 \\
& \Rightarrow 3 \lambda-6=0 \\
& \therefore \lambda=2
\end{aligned}
$

Hence, the answer is 2.

Example 2: Let the lines $L_1: \frac{x+5}{3}=\frac{y+4}{1}=\frac{z-\alpha}{-2}$ and $L_2: 3 x+2 y+z-2=0=x-3 y+2 z-13$ be coplanar. If the point $\mathrm{P}(\mathrm{a}, \mathrm{b}, \mathrm{c})$ on 11 is nearest to the point $\mathrm{Q}(-4,-3,2)$, then $|\mathrm{a}|+|\mathrm{b}|+|\mathrm{c}|$ is equal to
[JEE MAINS 2023]

Solution

$
\begin{aligned}
& (3 x+2 y+z-2)+\mu(x-3 y+2 z-13)=0 \\
& 3(3+\mu)+1 .(2-3 \mu)-2(1+2 \mu)=0 \\
& 9-4 \mu=0 \\
& \mu=\frac{9}{4} \\
& 4(-15-8+\alpha-2)+9(-5+12+2 \alpha-13)=0 \\
& -100+4 \alpha-54+18 \alpha=0 \\
& \Rightarrow \alpha=7
\end{aligned}
$
Let $P=(3 \lambda-5, \lambda-4,-2 \lambda+7)$
Direction ratio of $\mathrm{PQ}(3 \lambda-1, \lambda-1,-2 \lambda+5)$

$
\begin{aligned}
& \text { But } \mathrm{PQ} \perp C_1 \\
& \Rightarrow 3(3 \lambda-1)+1 \cdot(\lambda-1)-2(-2 \lambda+5)=0 \\
& \Rightarrow \lambda=1 \\
& P(-2,-3,5) \Rightarrow|a|+|b|+|c|=10
\end{aligned}
$

Hence, the answer is 10.

Example 3: The line, that is coplanar to the line $\frac{x+3}{-3}=\frac{y-1}{1}=\frac{z-5}{5}$, is

[JEE MAINS 2023]

Solution:
Condition of co-planarity

$
\left|\begin{array}{lll}
x_2-x_1 & a_1 & a_2 \\
y_2-y_1 & b_1 & b_2 \\
z_2-z_1 & c_1 & c_2
\end{array}\right|=0
$
Where$ a1, b1, c1$ are the direction cosine of $1^{\text {st }}$ line and a2, b2, c2 are the direction cosine of $2^{\text {st }}$ line.

Now. Solving options

Point $(-3, 1, 5)$ & point $(-1, 2, 5)$

$
\begin{aligned}
& \text { (1) }\left|\begin{array}{ccc}
-3 & 1 & 5 \\
1 & 2 & 5 \\
-2 & -1 & 0
\end{array}\right| \\
& =-3(5)-(10)+5(-1+4) \\
& =-15-10+15=-10
\end{aligned}
$
$
\begin{aligned}
& \text { (2)point }(-1,2,5) \\
& \left|\begin{array}{ccc}
-3 & 1 & 5 \\
-1 & 2 & 5 \\
-2 & -1 & 0
\end{array}\right| \\
& =3(5)-(10)+5(1+4) \\
& -25+5=0
\end{aligned}
$
$
\text { (3) point }(-1,2,5)
$
$
\begin{aligned}
& \left|\begin{array}{ccc}
-3 & 1 & 5 \\
-1 & 2 & 4 \\
-2 & -1 & 0
\end{array}\right| \\
& -3(4)-(8)+5(1+4) \\
& -12-8+25=5
\end{aligned}
$

(4) point $(-1,2,5)$
$\begin{aligned} & \left|\begin{array}{rrr}-3 & 1 & 5 \\ -1 & 2 & 5 \\ 4 & 1 & 0\end{array}\right| \\ & -3(-5)-(-20)+5(-1-8) \\ & 15+20-45=-10\end{aligned}$

Hence, the answer is -10

Example 4: Let the lines $\mathrm{L}_1: \overrightarrow{\mathbf{r}}=\lambda(\hat{i}+2 \hat{j}+3 \hat{k}), \lambda \in \mathbf{R}$ and $\mathrm{L}_2: \overrightarrow{\mathrm{r}}=(\hat{i}+3 \hat{j}+\hat{k})+\mu(\hat{i}+\hat{j}+5 \hat{k}) ; \mu \in \mathbf{R}$ intersect at the point S. If a plane $a x+$ by $-z+d=0$ passes through $S$ and is parallel to both the lines $L_1$ and $L_2$, then the value of $\mathrm{a}+\mathrm{b}+\mathrm{d}$ is equal to $\qquad$ [JEE MAINS 2022]

Solution:
$\begin{aligned} & L_1: \vec{r}=\lambda(\hat{i}+2 \hat{j}+3 \hat{k}), \lambda \in R \\ & L_2: \vec{r}=(\hat{i}+3 \hat{j}+\hat{k})+\mu(\hat{i}+\hat{j}+5 \hat{k})\end{aligned}$

From the given conditions, the plane contains both the lines

The normal vector is the cross-product of the direction vectors of both lines

$\begin{aligned} & \vec{n}=(i+2 j+3 k) \times(i+j+5 k) \\ & \vec{n}=(7 i-2 j-k)\end{aligned}$

It also passes through point (0,0,0) lying on line 1

So the plane is $7(x - 0) - 2(y - 0) - (z - 0) = 0$

Hence $a = 7, b = -2, c = -1, d = 0$

$a + b + d = 5$

Hence, the answer is $5$

Example 5: The largest value of a, for which the perpendicular distance of the plane containing the lines

$
\vec{r}=(\hat{\mathrm{i}}+\hat{\mathrm{j}})+\lambda(\hat{\mathrm{i}}+\mathrm{a} \hat{\mathrm{j}}-\hat{\mathrm{k}}) \text { and } \vec{r}=(\hat{\mathrm{i}}+\hat{\mathrm{j}})+\mu(-\hat{\mathrm{i}}+\hat{\mathrm{j}}-\mathrm{ak})
$

from the point $(2,1,4)$ is $\sqrt{3}$, is $\qquad$
[JEE MAINS 2022]

Solution:
Normal vector $\vec{n}$ of the plane

$
\begin{aligned}
& =\left|\begin{array}{rrr}
i & j & k \\
1 & a & -1 \\
-1 & 1 & -a
\end{array}\right| \\
& =\left(-\mathrm{a}^2+1\right) \mathrm{i}-(-\mathrm{a}-1) \mathrm{j}+(1+\mathrm{a}) \mathrm{k} \\
& =\left(1-\mathrm{a}^2\right) \mathrm{i}+(\mathrm{a}+1) \mathrm{j}+(\mathrm{a}+1) \mathrm{k} \\
& =(\mathrm{a}+1)[(1-\mathrm{a}) \mathrm{i}+\mathrm{j}+\mathrm{k}]
\end{aligned}
$

$\therefore \vec{n}$ is parallel to $(1-\mathrm{a}) \mathrm{i}+\mathrm{j}+\mathrm{k}$
$\therefore$ Equation of the plane is

$
\begin{aligned}
& (1-a)(x-1)+(y-1)+(z-0)=0 \\
& (1-a) x+y+z-1-(1-a)=0 \\
& (1-a) x+y+z+a-2=0
\end{aligned}
$
Distance from $(2,1,4)$

$\begin{aligned} & \frac{|2(\mid-\mathrm{a})+1+4+\mathrm{a}-2|}{\sqrt{(1-\mathrm{a})^2+1+1}}=\sqrt{3} \\ & \Rightarrow \frac{|-\mathrm{a}+5|}{\sqrt{1+\mathrm{a}^2-2 \mathrm{a}+2}}=\sqrt{3} \\ & \Rightarrow|5-\mathrm{a}|=\sqrt{3} \sqrt{\mathrm{a}^2-2 \mathrm{a}+3} \\ & \Rightarrow \mathrm{a}^2+25-10 \mathrm{a}=3\left(\mathrm{a}^2-2 \mathrm{a}+3\right) \\ & \Rightarrow \mathrm{a}^2-10 \mathrm{a}+25=3 \mathrm{a}^2-6 \mathrm{a}+9 \\ & \Rightarrow 2 \mathrm{a}^2+4 \mathrm{a}-16=0 \\ & \Rightarrow \mathrm{a}^2+2 \mathrm{a}-\mathrm{b}=0 \\ & \Rightarrow \mathrm{a}=2,-4 \\ & \therefore \text { Maximum } \mathrm{a}=2\end{aligned}$

Hence, the answer is 2

Summary

The coplanarity of two lines involves evaluating their direction vectors and checking if they lie within the same plane. Knowledge of the coplanarity of planes helps us solve geometric and arithmetic problems. Understanding of coplanarity helps us to solve and analyze real-life problems.