Cube roots of unity

Cube roots of unity are significant in various fields of mathematics, including algebra, number theory, and complex analysis. The cube root of unity is effective because it is cyclic in nature. They provide a fundamental example of roots of unity, which are essential in understanding polynomial equations, symmetries, and cyclic groups.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. What is Cube Root of Unity?
2. How To Find Cube Root Of Unity?
3. Product of Cube Roots Of Unity
4. Sum of Cube Roots of Unity
5. Euler’s Formula
6. Deriving Cube Roots of Unity by De Moivre's Theorem
7. Properties of Cube roots of unity

In this article, we will cover the concept of the cube root of unity. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.

What is Cube Root of Unity?

The cube root of unity is represented as $\sqrt[3]{1}$ and it has three roots. The three cube roots of unity are $1,\omega ,{\omega }^2$, which on multiplication answers unity (1). Among the roots of the cube roots of unity, one root is a real root and the other two roots are imaginary roots. The values of the imaginary cube roots of unity are as follows.

- $\omega =(-1+i\sqrt{3})/2$

- ${\omega }^2=(-1-i\sqrt{3})/2$

How To Find Cube Root Of Unity?

Let $z$ be the cube root of unity (1)
So, $z^3=1$
$\Rightarrow {\mathrm{z}}^3-1=0$
$\Rightarrow (z-1)(z^2+z+1)=0$
$\Rightarrow \mathrm{z}-1=0$ or ${\mathrm{z}}^2+\mathrm{z}+1=0$
$\therefore \mathrm{z}=1\text{ or }\mathrm{z}=\frac{-1\pm \sqrt{(1-4)}}{2}=\frac{-1\pm \mathrm{i}\sqrt{3}}{2}$
Therefore, $\mathrm{z}=1,\mathrm{z}=\frac{-1+\mathrm{i}\sqrt{3}}{2}$ and $\mathrm{z}=\frac{-1-\mathrm{i}\sqrt{3}}{2}$
If the second root is represented by $\mathit{\omega }$, then the third root will be represented by ${\mathit{\omega }}^2$ (we can check that by squaring the second root, we get the third root)

$\omega =\frac{-1+\mathrm{i}\sqrt{3}}{2},{\omega }^2=\frac{-1-\mathrm{i}\sqrt{3}}{2}$
So, $1,\omega ,{\omega }^2$ are cube roots of unity and $\omega ,{\omega }^2$ are the non-real complex root of unity.

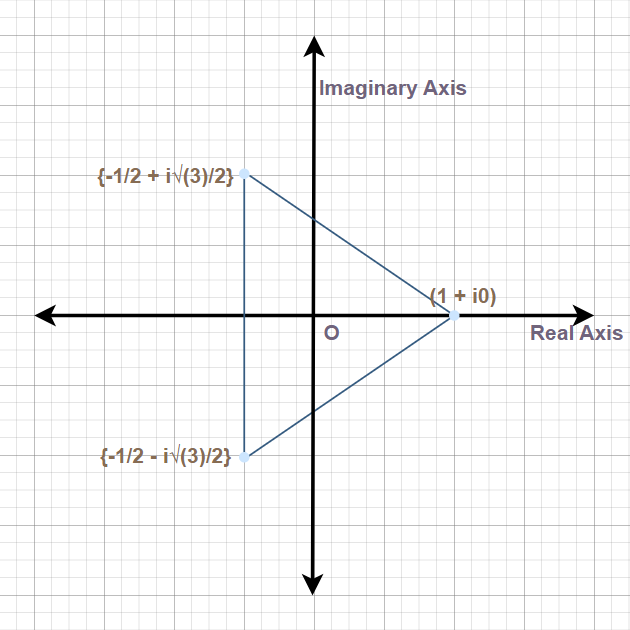
Product of Cube Roots Of Unity

The product of the cube roots of unity is equal to 1. This can be understood from the below expression.

$\begin{array}{rl}& 1\times \omega \times {\omega }^2=1\times (-1+i\sqrt{}3)/2\times (-1-i\sqrt{}3)/2\\ & =((-1{)}^2-(i\sqrt{}3{)}^2)/(2\times 2)\\ & =(1-3i^2)/4\\ & =(1-3(-1))/4\\ & =4/4\\ & =1\\ & \therefore 1\times \omega \times {\omega }^2=1\end{array}$

Sum of Cube Roots of Unity

The sum of the cube roots of unity is equal to zero. This can be observed in the below expression.

$\begin{array}{rl}& 1+\omega +{\omega }^2=1+(-1+i\sqrt{}3)/2+(-1-i\sqrt{}3)/2=1+(-1+i\sqrt{}3-1-i\sqrt{}3)/2,=1+(-2/2)=1-1=0\\ & \therefore 1+\omega +{\omega }^2=0\end{array}$

Euler’s Formula

It shows the relation between the imaginary power of an exponent and sine and cosine, and is given by:

$e^{ix}=\cos x+i\sin x$

The cube roots of unity are $1,\omega ,{\omega }^2$, where:

$\omega =\frac{-1+i\sqrt{3}}{2},{\omega }^2=\frac{-1-i\sqrt{3}}{2}$

Using Euler's Formula, we can conclude the following:
- $1=e^{0i}$

$(\text{ as }{e}^{0i}=\cos (0)+i\sin (0)=1+i(0)=1)$

- $\omega =e^{2\pi i/3}$

$(\text{ as }{e}^{2\pi i/3}=\cos (2\pi /3)+i\sin (2\pi /3)=\frac{-1+i\sqrt{3}}{2})$

- ${\omega }^2=e^{4\pi i/3}$

$(\text{ as }{e}^{4\pi i/3}=\cos (4\pi /3)+i\sin (4\pi /3)=\frac{-1-i\sqrt{3}}{2})$

Deriving Cube Roots of Unity by De Moivre's Theorem

$\sqrt[3]{1}$ can be written as $1^{1/3}$. In complex numbers, we have a theorem called De Moivre's Theorem, which is very useful in finding the real and complex roots of a real/complex number. This theorem states:

$(a+ib{)}^n=(r(\cos \theta +i\sin \theta ){)}^n=r^n(\cos n\theta +i\sin n\theta ),\text{ where }n\in \mathbb{Z}$

Let us assume that $a+ib=1=1+i(0)$. Then we have $a=1$ and $b=0$.
Now,

$\begin{array}{rl}& r=\sqrt{a^2+b^2}=\sqrt{1^2+0^2}=1\\ & \theta ={\tan }^{-1}\left|\frac{b}{a}\right|={\tan }^{-1}\left|\frac{0}{1}\right|=0\end{array}$

We can write this angle as $0+2n\pi$, where $n=0,1,2$ (since we need to find three roots, three integer values are taken for $n$ ).

By substituting these values in De Moivre's theorem along with substituting $n=1/3$ :

$\begin{array}{c}(1+i(0){)}^{1/3}=1^{1/3}(\cos \frac{2n\pi }{3}+i\sin \frac{2n\pi }{3}),\text{ where }n=0,1,2\\ \Rightarrow 1^{1/3}=\cos \frac{2n\pi }{3}+i\sin \frac{2n\pi }{3},\text{ where }n=0,1,2\end{array}$

Finding the Cube Roots
- When $n=0$ :

$1^{1/3}=\cos 0+i\sin 0=1+i(0)=1$

- When $n=1$ :

$1^{1/3}=\cos \frac{2\pi }{3}+i\sin \frac{2\pi }{3}=-\frac{1}{2}+i\frac{\sqrt{3}}{2}=\frac{-1+i\sqrt{3}}{2}(=\omega )$

- When $n=2$ :

$1^{1/3}=\cos \frac{4\pi }{3}+i\sin \frac{4\pi }{3}=-\frac{1}{2}-i\frac{\sqrt{3}}{2}=\frac{-1-i\sqrt{3}}{2}(={\omega }^2)$

Thus, the cube roots of unity by De Moivre's theorem are:

$1,\frac{-1+i\sqrt{3}}{2},\frac{-1-i\sqrt{3}}{2}$

Properties of Cube roots of unity

i) $1+\omega +{\omega }^2=0$ and ${\omega }^3=1$ (Using sum and product of roots relations for the equation $z^3-1=0$ )
ii) To find ${\omega }^n$, first we write $\omega$ in multiple of 3 with the remainder being 0 or 1 or 2.

Now ${\omega }^n={\omega }^{3q+r}={\left({\omega }^3\right)}^q\cdot {\omega }^r={\omega }^r$ (Where r is from $0,1,2)$

$\text{ Eg, }{\omega }^{121}={\omega }^{3.40+1}={\left({\omega }^3\right)}^{40}\cdot {\omega }^1=\omega$

iii) $|\omega |=\left|{\omega }^2\right|=1,\arg (\omega )=2\pi /3,\arg \left({\omega }^2\right)=4\pi /3$ or $-2\pi /3$
iv) We can see that $\omega$ and ${\omega }^2$ differ by the minus sign of the imaginary part hence
v) Cube roots of -1 are $-1,-\omega ,-{\omega }^2$

vi) The cube roots of unity when represented on the complex plane have their point on vertices of a triangle circumscribed by a unit circle whose one vertices lies on the+ve X-axis.

Summary

The cube root of unity is an important aspect of complex numbers. Due to its cyclic property, it helps the fast calculation of high-power complex numbers. The main applications of the cube root of unity are solving polynomial functions, Fourier transform, group theory, and number theory.

Solved Examples Based On the Cube Root of Unity

Example 1: ${(\frac{-1}{2}+\frac{i\sqrt{3}}{2})}^{100}+{(\frac{-1}{2}-\frac{i\sqrt{3}}{2})}^{200}$ equals

Solution:

As we learned in

Cube roots of unity -
$z=(1{)}^{\frac{1}{3}}\Rightarrow z=\cos \frac{2k\pi }{3}+i\sin \frac{2k\pi }{3}$

$\mathrm{k}=0,1,2$ so z gives three roots

$\Rightarrow 1,\frac{-1}{2}+i\frac{\sqrt{3}}{2}(\omega ),\frac{-1}{2}-i\frac{\sqrt{3}}{2}\left({\omega }^2\right)$

wherein
$\omega =\frac{-1}{2}+\frac{i\sqrt{3}}{2}\cdot {\omega }^2=\frac{-1}{2}-\frac{i\sqrt{3}}{2},{\omega }^3=1.1+\omega +{\omega }^2=0$

1. $\omega .{\omega }^2$ are cube roots of unity.
given is $\to w^{100}+{\left(w^3\right)}^{200}=w^{100}+w^{400}$
$={\left(w^3\right)}^{33}\cdot {\left(w^3\right)}^{153}\cdot w^{15}=2w=-1+i\sqrt{3}$

Hence, the answer is $-1+i\sqrt{3}$

Example 2: If $\alpha$ and $\beta$ are the roots of the equation $x^2-x+1=0$ then ${\alpha }^{2009}+{\beta }^{2009}=$

Solution:

As we have learned

Roots of Quadratic Equation -

$\alpha =\frac{-b+\sqrt{b^2-4ac}}{2a}$

$\beta =\frac{-b-\sqrt{b^2-4ac}}{2a}$
- wherein

$a{x}^2+bx+c=0$

is the equation

$a,b,c\in R,a\ne 0$

Cube roots of unity -

$z=(1{)}^{\frac{1}{3}}\Rightarrow z=\cos \frac{2k\pi }{3}+i\sin \frac{2k\pi }{3}$

$k=0,1,2$ so $z$ gives three roots

$\Rightarrow 1,\frac{-1}{2}+i\frac{\sqrt{3}}{2}(\omega ),\frac{-1}{2}-i\frac{\sqrt{3}}{2}\left({\omega }^2\right)$

- wherein
$\omega =\frac{-1}{2}+\frac{i\sqrt{3}}{2}\cdot {\omega }^2=\frac{-1}{2}-\frac{i\sqrt{3}}{2}\cdot {\omega }^3=1.1+\omega +{\omega }^2=0$

1. $\omega ,{\omega }^2$ are cube roots of unity.

$\alpha ,\beta =\frac{1\pm \sqrt{-3}}{2}=\frac{1\pm \sqrt{3i}}{2}=-\left(\frac{-1\pm \sqrt{3i}}{2}\right)=-\omega ,-{\omega }^2$

${\alpha }^{2009}+{\beta }^{200}$
$5^{20n}+{(-w^2)}^{200}$

$=-{\omega }^2-\omega =-({\omega }^2+\omega )=-(-1)=1$
Hence, the answer is 1.

Example 3: Let $z_0$ be a root of the quadratic equation, $x^2+x+1=0$. If $z=3+6i{z}_0^{81}-3i{z}_0^{93}$ then arg z is equal to :

Solution:

Definition of Argument/Amplitude of z in Complex Numbers -

$\theta ={\tan }^{-1}\left|\frac{y}{x}\right|,z\ne 0$

$\theta ,\pi -\theta ,-\pi +\theta ,-\theta$ are Principal Arguments if z lies in the first, second, third, or fourth quadrant respectively.

now,

Cube roots of unity -

$z=(1{)}^{\frac{1}{3}}\Rightarrow z=\cos \frac{2k\pi }{3}+i\sin \frac{2k\pi }{3}$

k=0,1,2 so z gives three roots

$\Rightarrow 1,\frac{-1}{2}+i\frac{\sqrt{3}}{2}(\omega ),\frac{-1}{2}-i\frac{\sqrt{3}}{2}\left({\omega }^2\right)$

- wherein

$\omega =\frac{-1}{2}+\frac{i\sqrt{3}}{2},{\omega }^2=\frac{-1}{2}-\frac{i\sqrt{3}}{2},{\omega }^3=1,1+\omega +{\omega }^2=0$

$1,\omega ,{\omega }^2$ are cube roots of unity.

Quadratic Equation

$x^2+x+1=0$, roots are, $\omega$ and $w^2$ where $\omega$ is the cube root of unity.

$z=3+6i{\left(z_0\right)}^{81}-3i{\left(z_0\right)}^{93}$

$z_0=\omega$ and ${\omega }^2$

$z=3+6i(\omega {)}^{81}-3i(\omega {)}^{93}$

$z=3+3i\because {\omega }^3=1$

$\arg (z)=\frac{\pi }{4}$

Hence, the answer is $\pi /4$.

Example 4: Let $z={(\frac{\sqrt{3}}{2}+\frac{i}{2})}^5+{(\frac{\sqrt{3}}{2}-\frac{i}{2})}^5$. If $R(z)$ and $I(z)$ respectively denote the real and imaginary parts of z, then:

1) $R(z)<0$ and $I(z)>0$
2) $R(z)>0$ and $I(z)>0$
3) $R(z)=-3$
4) $I(z)=0$

Solution:

$\begin{array}{rl}& z={(\frac{\sqrt{3}}{2}+\frac{i}{2})}^5+{(\frac{\sqrt{3}}{2}-\frac{i}{2})}^3\\ & z={\left(e^{i\frac{\pi }{6}}\right)}^5+{\left(e^{-i\frac{\pi }{4}}\right)}^3\\ & =\cos \frac{5\pi }{6}+i\sin \frac{5\pi }{6}+\cos \frac{5\pi }{6}-i\sin \frac{5\pi }{6}\\ & =2\cos \frac{5\pi }{6}<0\\ & \mathrm{Im}(z)=0\end{array}$

Hence, the answer is the option (4).

Example 5: Le$a=\frac{-1+i\sqrt{3}}{2}a=(1+a)\sum _{k=0}^{100}{a}_{\text{and }}^{2k}b=\sum _{i=0}^{100}{a}^{3k}$en a and b are the roots of the quadratic equation:

1) $x^2+101x+100=0$

2) $x^2+102x+101=0$

3) $x^2-102x+101=0$

4) $x^2-101x+100=0$

Solution:

Now,

$\alpha =\omega$

$b=1+{\omega }^3+{\omega }^6+\dots \dots {\omega }^{300}=101$

$a=(1+\omega )(1+{\omega }^2+{\omega }^4+{\omega }^6\dots +{\omega }^{200})$

$a=(1+\omega )\frac{({\omega }^{2(101)}-1)}{{\omega }^2-1}=\frac{1-{\omega }^2}{1-{\omega }^2}=1$

Now, the equation with roots 1 and 101 is

$\begin{array}{rl}& x^2-(1+101)x+101\ast 1=0\\ & x^2-102x+101=0\end{array}$

Hence, the answer is option (3).