Equation of the Plane Bisecting the Angle Between Two Planes

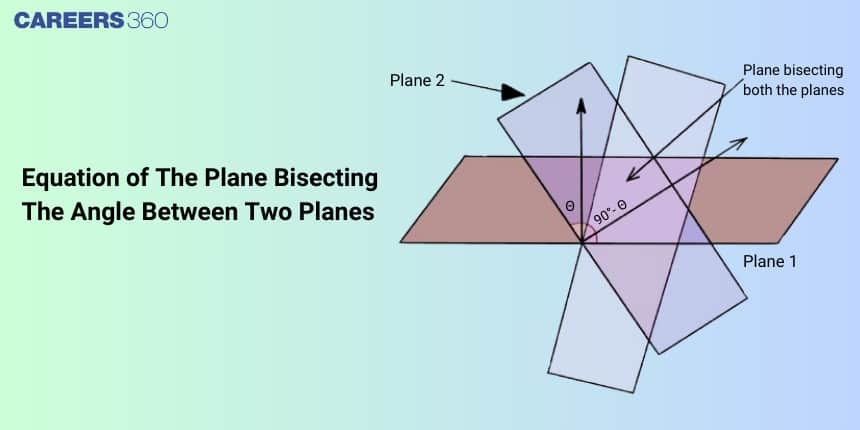
Any three points that do not all lie on the same line is a unique plane that passes through these points. Just as a line is determined by two points, a plane is determined by three. The angle between two Planes is determined by the angle between the normals of the two planes. This article is about the equation of the plane bisecting the angle between two planes which falls under the broader category of Three Dimensional Analytical Geometry.

The equation of the planes bisecting the angle between the planes can be computed in two ways, the Cartesioan Form and the Veector Form.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

Cartesian Form

Equation of the planes bisecting the angle between the planes $a_1 x+b_1 y+c_1 z+$ $d_1=0$ and $a_2 x+b_2 y+c_2 z+d_2=0$ is

$
\frac{a_1 x+b_1 y+c_1 z+d_1}{\sqrt{a_1^2+b_1^2+c_1^2}}= \pm \frac{a_2 x+b_2 y+c_2 z+d_2}{\sqrt{a_2^2+b_2^2+c_2^2}}
$

Proof:
Given planes are

$
\begin{array}{ll}
& a_1 x+b_1 y+c_1 z+d_1=0 . . . (i)\\
\text { and } & a_2 x+b_2 y+c_2 z+d_2=0 . . . (ii)
\end{array}
$

Let $P(x, y, z)$ be a point on the plane bisecting the angle between planes (i) and (ii).

Let PL and PM be the length of perpendiculars from P to planes (i) and (ii).

$\begin{array}{rlrl}\therefore & P L & =P M \\ \Rightarrow & \left|\frac{a_1 x+b_1 y+c_1 z+d_1}{\sqrt{a_1^2+b_1^2+c_1^2}}\right| & =\left|\frac{a_2 x+b_2 y+c_2 z+d_2}{\sqrt{a_2^2+b_2^2+c_2^2}}\right| \\ \frac{a_1 x+b_1 y+c_1 z+d_1}{\sqrt{a_1^2+b_1^2+c_1^2}} & = \pm \frac{a_2 x+b_2 y+c_2 z+d_2}{\sqrt{a_2^2+b_2^2+c_2^2}}\end{array}$

This is the equation of planes bisecting the angles between the planes (i) and (ii).

Vector Form

Equation of the planes bisecting the angle between the planes $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_1=d_1$ and $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_2=d_2$ is

$
\left|\frac{\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_1-d_1}{\overrightarrow{\mathbf{n}}_1}\right|=\left|\frac{\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_2-d_2}{\overrightarrow{\mathbf{n}}_2}\right|
$

Bisector of the Angle between the Two Planes Containing the Origin

Let the equation of the two planes be

$
\begin{array}{ll}
& a_1 x+b_1 y+c_1 z+d_1=0 . . . (i) \\
\text { and } & a_2 x+b_2 y+c_2 z+d_2=0 . . . (ii)
\end{array}
$

where $\mathrm{d}_1$ and $\mathrm{d}_2$ are positive.
Then the equation of the bisector of the angle between the planes (i) and (ii) containing the origin is

$
\frac{\mathrm{a}_1 \mathrm{x}+\mathrm{b}_1 \mathrm{y}+\mathrm{c}_1 \mathrm{z}+\mathrm{d}_1}{\sqrt{\mathrm{a}_1^2+\mathrm{b}_1^2+\mathrm{c}_1^2}}=\frac{\mathrm{a}_2 \mathrm{x}+\mathrm{b}_2 \mathrm{y}+\mathrm{c}_2 \mathrm{z}+\mathrm{d}_2}{\sqrt{\mathrm{a}_2^2+\mathrm{b}_2^2+\mathrm{c}_2^2}}
$

Bisector of the Acute and Obtuse Angle between Two Planes

Let the equation of the two planes be

$
\begin{aligned}
& a_1 x+b_1 y+c_1 z+d_1=0 \\
& a_2 x+b_2 y+c_2 z+d_2=0
\end{aligned}
$

1. If $a_1 a_2+b_1 b_2+c_1 c_2>0$, then the equation of the bisector of the obtuse angle is,

$
\frac{a_1 x+b_1 y+c_1 z+d_1}{\sqrt{a_1^2+b_1^2+c_1^2}}=\frac{a_2 x+b_2 y+c_2 z+d_2}{\sqrt{a_2^2+b_2^2+c_2^2}}
$

2. If $a_1 a_2+b_1 b_2+c_1 c_2<0$, then the equation of the bisector of the obtuse angle is,

$
\frac{a_1 x+b_1 y+c_1 z+d_1}{\sqrt{a_1^2+b_1^2+c_1^2}}=-\frac{a_2 x+b_2 y+c_2 z+d_2}{\sqrt{a_2^2+b_2^2+c_2^2}}
$

Recommended Video Based on Equation of the Plane Bisecting the Angle Between Two Planes

Solved Examples Based on Equation of The Plane Bisecting the Angle Between Two Planes:

Example 1: Equation of plane bisecting the angle between the planes $2 x-y+2 z-1=0$ and $x+2 y-2 z+1=0$ is:
1) $3 x+y=2$
2) $x+3 y-4 z-2=0$
3) $x-3 y+4 z-2=0$
4) $3 x+y=1$

Solution

As we have learned

Angle bisector of planes (cartesian form) -
Equation of plane bisecting the angle between the planes

$
a x+b y+c z+d=0
$

$a_1 x+b_1 y+c_1 z+d_1=0$ is

$
\frac{a x+b y+c z+d}{\sqrt{a^2+b^2+c^2}}= \pm \frac{a_1 x+b_1 y+c_1 z+d_1}{\sqrt{a_1^2+b_1^2+c_1^2}}
$

The equation of planes will be

$
\begin{aligned}
& \frac{2 x-y+2 z-1}{3}= \pm \frac{x+2 y-2 z+1}{3} \\
& x-3 y+4 z-2=0 \text { and } 3 x+y=0
\end{aligned}
$
Hence, the answer is the option (3).

Example 2: The equation of obtuse angle bisector plane of $3 x-2 y-6 z+1=0$ and $2 x-3 y+6 z-2=0$ is:
1) $5 x-5 y-1=0$
2) $x+y-12 z+3=0$
3) $x-y+12 z-3=0$
4) $5 x+5 y+1=0$

Solution

As we have learned
Bisector of the obtuse and acute angle between two planes -
Let the planes be
$a x+b y+c z+d=0$ and
$a_1 x+b_1 y+c_1 z+d_1=0
$

Where $d$ and $d_1$ are positive

If $a_1 a+b_1 b+c_1 c>0$ the angle bisector with the + sign is an obtuse angle bisector and the angle bisector with the - sign is an acute angle bisector.

If $a_1 a+b_1 b+c_1 c<0$ so, the angle bisector with the - sign is the obtuse angle bisector and the angle bisector with the + sign is the acute angle bisector.

Planes can be written as $3 x-2 y-6 z+1=0$ and $-2 x+3 y-6 z+2=0$, Now $3(-2)+(-2) 3+$ $(-6)(-6)=24>0$

So obtuse bisector will be given by

$
\begin{aligned}
& (3 x-2 y-6 z+1) / 7=(2 x-3 y+6 z-2) / 7 \\
& x+y-12 z+3=0
\end{aligned}
$

Hence, the answer is the option (2).

Example 3: A vector $\vec{a}=\alpha \hat{i}+2 \hat{j}+\beta \hat{k}(\alpha, \beta \in R) \quad$ lies in the plane of the vectors, $\vec{b}=\hat{i}+\hat{j}$ and $\vec{c}=\hat{i}-\hat{j}+4 \hat{k}$. If $\vec{a}$ bisects the angle between $\vec{b}$ and $\vec{c}$, then:
1) $\vec{a} \cdot \hat{i}+3=0$
2) $\vec{a} \cdot \hat{k}+4=0$
3) $\vec{a} \cdot \hat{i}+1=0$
4) $\vec{a} \cdot \hat{k}+2=0$

Solution

Equation of The Plane Bisecting the Angle Between Two Planes -
angle bisector can be $\vec{a}=\vec{a}=\lambda(\hat{b}+\hat{c})$ or $\vec{a}=\mu(\hat{b}-\hat{c})$

$
\begin{aligned}
& \overrightarrow{\mathrm{a}}=\lambda\left(\frac{\hat{\mathrm{i}}+\hat{\mathrm{j}}}{\sqrt{2}}+\frac{\hat{\mathrm{i}}-\hat{\mathrm{j}}+4 \hat{\mathrm{k}}}{3 \sqrt{2}}\right)=\frac{\lambda}{3 \sqrt{2}}[3 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+\hat{\mathrm{i}}-\hat{\mathrm{j}}+4 \hat{\mathrm{k}}] \\
& =\frac{\lambda}{3 \sqrt{2}}[4 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+4 \hat{\mathrm{k}}]
\end{aligned}
$

Compare it with $\overrightarrow{\mathrm{a}}=\alpha \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\beta \hat{\mathrm{k}}$

$
\begin{aligned}
& \frac{2 \lambda}{3 \sqrt{2}}=2 \Rightarrow \lambda=3 \sqrt{2} \\
& \overrightarrow{\mathrm{a}}=4 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+4 \hat{\mathrm{k}}
\end{aligned}
$

Not in option so now consider $\vec{a}=\mu\left(\frac{\hat{i}+\hat{j}}{\sqrt{2}}-\frac{\hat{i}-\hat{j}+4 \hat{k}}{3 \sqrt{2}}\right)$

$
\begin{aligned}
\overrightarrow{\mathrm{a}} & =\frac{\mu}{3 \sqrt{2}}(3 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-\hat{\mathrm{i}}+\hat{\mathrm{j}}-4 \hat{\mathrm{k}}) \\
& =\frac{\mu}{3 \sqrt{2}}(2 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}-4 \hat{\mathrm{k}})
\end{aligned}
$

Compare it with $\overrightarrow{\mathrm{a}}=\alpha \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\beta \hat{\mathrm{k}}$

$
\begin{aligned}
& \frac{4 \mu}{3 \sqrt{2}}=2 \Rightarrow \mu=\frac{3 \sqrt{2}}{2} \\
& \overrightarrow{\mathrm{a}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-2 \hat{\mathrm{k}} \\
& \overrightarrow{\mathrm{a}} \cdot \hat{\mathrm{k}}+2=0 \\
& -2+2=0
\end{aligned}
$

Hence, the answer is the option 4.

Example 4: A plane which bisects the angle between the two given planes $2 x-y+2 z-4=0$ and $x+2 y+2 z-2=0$, passes through the points:
1) $(1,-4,1)$
2) $(1,4,-1)$
3) $(2,4,1)$
4) $(2,-4,1)$

Solution
$
\left|\frac{x+2 y+2 z-2}{3}\right|=\left|\frac{2 x-y+2 z-4}{3}\right|
$

The required equations of planes are

$
x-3 y-2=0
$

and

$
3 x+y+4 z-6=0
$

Now, substituting the options we will get, the point $(2,-4,1)$.
Hence, the answer is the option 4.

Example 5: Equation of one of the planes bisecting the angle between planes $\vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})=1$ and $\vec{r} \cdot(\hat{i}-\hat{j}-\hat{k})=2$ is:
1) $\vec{r} \cdot(\hat{i}+\hat{j})=\frac{3}{2}$
2) $\vec{r} \cdot(\hat{i}-\hat{j})=\frac{3}{2}$
3) $\vec{r} \cdot(\hat{i}+\hat{j}+\hat{k})=\frac{-1}{2}$
4) $\vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})=\frac{-1}{2}$

Solution

The equation of planes will be

$
\frac{\vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})-1}{\sqrt{3}}= \pm \frac{\vec{r} \cdot(\hat{i}-\hat{j}-\hat{k})-2}{\sqrt{3}}
$

Taking positive sign

$
\vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})= \pm(\vec{r} \cdot(\hat{i}-\hat{j}-\hat{k})-2)+1
$

Taking + and - signs one by one

$
\begin{aligned}
& \vec{r} \cdot(2 \hat{k})=-1, \vec{r} \cdot(2 \hat{i}-2 \hat{j})=3 \\
& \vec{r} \cdot(\hat{k})=\frac{-1}{2}, \vec{r} \cdot(\hat{i}-\hat{j})=\frac{3}{2}
\end{aligned}
$
Hence, the answer is the option (2).

Summary
The equation of the plane bisecting the angle between the planes in cartesian form is $\frac{a_1 x+b_1 y+c_1 z+d_1}{\sqrt{a_1^2+b_1^2+c_1^2}}= \pm \frac{a_2 x+b_2 y+c_2 z+d_2}{\sqrt{a_2^2+b_2^2+c_2^2}}$ and in vector form is $
\left|\frac{\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_1-d_1}{\overrightarrow{\mathbf{n}}_1}\right|=\left|\frac{\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_2-d_2}{\overrightarrow{\mathbf{n}}_2}\right|
$.