Euler Form of Complex Number

There are two forms of complex numbers one is polar form and the other one is euler form. In this article, we learned about the Euler form of complex numbers. It is also expressed in terms of modulus and arguments of complex numbers. The main application of the polar form is in the multiplication and division, powers and roots, signal processing, and the control system of responses. It is generally represented as $r$. $e^{i \theta}$

This Story also Contains

1. Complex Numbers
2. Euler's Formula
3. Euler form of a complex number
4. Applications of Euler form
5. Euler's identity

In this article, we will cover the concept of the Euler form of a complex number. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of two questions have been asked on this concept, one in 2020, and one in 2021.

Complex Numbers

The number which has no real meaning then these numbers are represented in complex forms. The general form of complex numbers are $a+i b$ where i is iota or$\sqrt{-1}$.

A number of the form$a+i b$ is called a complex number (where a and b are real numbers and i is iota). We usually denote a complex number by the letter $\mathrm{z}, \mathrm{z}_1, \mathrm{z}_2$ etc

For example$z=5+2 i$ is a complex number.

5 here is called the real part and is denoted by Re(z), and 2 is called the imaginary part and is denoted by Im(z)

Euler's Formula

Euler's formula was given by Leonhard Euler, a Swiss mathematician. There are two types of Euler's formulas:

• For complex analysis: It is a key formula used to solve complex exponential functions. Euler's formula is also sometimes known as Euler's identity. It is used to establish the relationship between trigonometric functions and complex exponential functions.
• For polyhedra: For any polyhedron that does not self-intersect, the number of faces, vertices, and edges is related in a particular way, and that is given by Euler's formula or also known as Euler's characteristic.

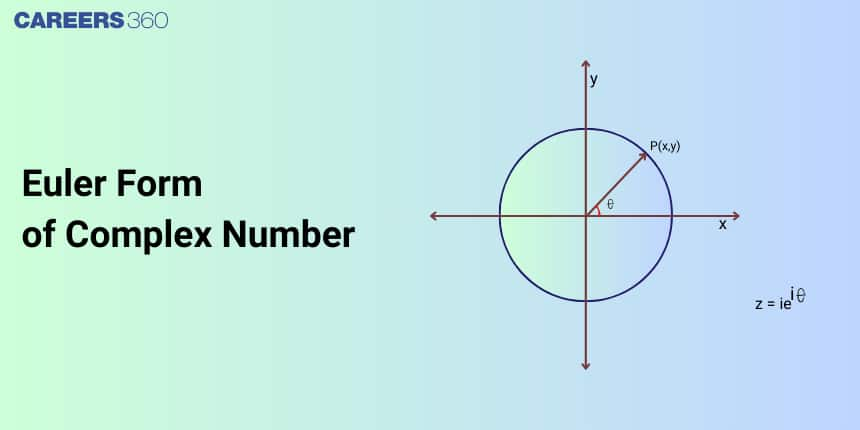
Euler form of a complex number

Euler’s formula establishes the fundamental relationship between trigonometric functions and exponential functions. Geometrically, it can be thought of as a way of bridging two representations of the same unit complex number in the complex plane. It is an extremely convenient representation that leads to simplifications in a lot of calculations.

The polar form of complex number$z=r(\cos \theta+i \sin \theta)$

In Euler form$(\cos \theta+i \sin \theta)$) part of the polar form of complex numbers is represented by e $^{\mathrm{i \theta}}$. So, $\mathrm{z}=\mathrm{r}(\cos \theta+\mathrm{i} \sin \theta)$ is witten as $\mathrm{r} . \mathrm{e}^{\mathrm{i \theta}}$ in Euler's Form

Derivation

We know the expansion of $e^x$ is

The expansion of $e^x$ is

$
\mathrm{e}^{\mathrm{x}}=1+\frac{\mathrm{x}}{1!}+\frac{\mathrm{x}^2}{2!}+\frac{\mathrm{x}^3}{3!}+\ldots
$
Replacing x by ix

$
\begin{aligned}
& e^{i x}=1+\frac{i x}{1!}+\frac{(i x)^2}{2!}+\frac{(i x)^3}{3!}+\frac{(i x)^4}{4!}+\ldots \\
& e^{i x}=1+\frac{i x}{1!}-\frac{x^2}{2!}-\frac{i x^3}{3!}+\frac{x^4}{4!}+\ldots+
\end{aligned}
$

rearranging the terms, we have

$
e^{i x}=\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}\right)+i\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}\right)
$
We notice that first bracket is the expansion of $\sin x$ and 2 nd bracket is the expansion of $\cos x$, so we have $e^{i x}=\sin x+i \cos x$

So, $e^{i \theta}=\cos \theta+i \sin \theta$ and

$
e^{-i \theta}=\cos \theta-i \sin \theta
$

Euler forms make algebra very simple for complex numbers in cases where multiplication, division or powers of complex numbers are involved. Any complex number can be expressed as

$z=x+i y$ (Cartesian Form)

$z=r(\cos \theta+i \sin \theta)$ (Polar Form)

$\mathrm{z}=|\mathrm{z}| \mathrm{e}^{\mathrm{i} \theta}$ (Eular's Form)

Applications of Euler form

1. Multiplication of two complex numbers

Let $\mathrm{z}=|\mathrm{z}| \mathrm{e}^{\mathrm{i} \theta_1}$
And $\mathrm{w}=|\mathrm{w}| \mathrm{e}^{\mathrm{i} \theta_2}$
Multiplying these two number
$\mathrm{z} \cdot \mathrm{w}=|\mathrm{z}| \mathrm{e}^{\mathrm{i} \theta_1} \cdot|\mathrm{w}| \mathrm{e}^{\mathrm{i} \theta_2}$
$=|\mathrm{z}| \cdot|\mathrm{w}| \mathrm{e}^{\mathrm{i}\left(\theta_1+\theta_2\right)}$

2. Division also can be done in the same way

$\begin{aligned} & \mathrm{z}=|\mathrm{z}| \mathrm{e}^{\mathrm{i} \theta_1} \text { and } \mathrm{w}=|\mathrm{w}| \mathrm{e}^{\mathrm{i} \theta_2} \text { be two complex number } \\ & \therefore \frac{\mathrm{z}}{\mathrm{w}}=\frac{|\mathrm{z}|}{|\mathrm{w}|} \mathrm{e}^{\mathrm{i}\left(\theta_1-\theta_2\right)}\end{aligned}$

3. The logarithm of Complex Number

$\begin{aligned} & \mathrm{z}=|\mathrm{z}| \mathrm{e}^{\mathrm{i} \theta} \\ & \log _{\mathrm{e}}(\mathrm{z})=\log _{\mathrm{e}}\left(|\mathrm{z}| \mathrm{e}^{\mathrm{i} \theta}\right) \\ & \log _{\mathrm{e}}(\mathrm{z})=\log _{\mathrm{e}}(|\mathrm{z}|)+\log _{\mathrm{e}}\left(\mathrm{e}^{\mathrm{i} \theta}\right) \\ & \log _{\mathrm{e}}(\mathrm{z})=\log _{\mathrm{e}}(|\mathrm{z}|)+\mathrm{i} \arg (\mathrm{z})\end{aligned}$

Euler's identity

Euler’s identity is often considered the most beautiful mathematics equation. It is written as $e^{i \pi}=-1$

Among these, three types of numbers are represented: integers, irrational, and imaginary. Three basic mathematical operations are also represented: addition, multiplication, and exponentiation.

We obtain Euler’s identity by starting with Euler’s formula $e^{i x}=\cos x+i \sin x$, setting $x=\pi$ and sending the subsequent −1 to the left-hand side. The intermediate form $e^{i \pi}=-1$ is common in the context of a trigonometric unit circle in the complex plane.

Summary

We concluded that a complex number's Euler form is simpler than another. It helps in simplify the complex problems of complex numbers in the simplest way. Understanding the Euler form of complex numbers provides powerful tools for performing complex arithmetic and analyzing various physical and engineering systems.

Solved Examples Based On the Eular Form of a Complex Number

Example 1: If $\alpha$ and $\beta$ are the roots of the equation $\frac{1}{i Z}-i Z=2(\sin \theta-i \cos \theta)$ where $0<\theta<\pi$ and $i=\sqrt{-1}$, and z is complex numbers, then the value of $|\alpha-i|+|\beta-i|$

Solution:

$\frac{1}{i Z}-i Z=2(\sin \theta-i \cos \theta)$

Multiply with "i" both side

$\frac{1}{Z}-i^2 Z=2\left(i \sin \theta-i^2 \cos \theta\right)$

$\frac{1}{Z}+Z=2(\cos \theta+i \sin \theta)$

$\frac{1}{Z}+Z=2 e^{i \theta}$

$Z^2-2 Z e^{i \theta}+1=0$

$\begin{aligned} & Z=\frac{2 e^{i \theta} \pm \sqrt{4 e^{2 i \theta}}-4}{2} \\ & Z=e^{i \theta} \pm \sqrt{e^{2 i \theta}-1}\end{aligned}$

$\begin{aligned} & Z=e^{i \theta} \pm \sqrt{e^{i \theta} \cdot 2 i \sin \theta} \\ & Z-i=e^{i \theta}-i \pm \sqrt{e^{i \theta} \cdot 2 i \sin \theta} \\ & Z-i=e^{i \theta}-e^{i \frac{\pi}{2}} \pm \sqrt{e^{i\left(\theta+\frac{\pi}{2}\right)} \cdot 2 \sin \theta}\end{aligned}$

$\begin{aligned} & Z-i=e^{i\left(\frac{\theta}{2}+\frac{\pi}{4}\right)} \cdot 2 i \sin \left(\frac{\theta}{2}-\frac{\pi}{4}\right) \pm e^{i\left(\frac{\theta}{2}+\frac{\pi}{4}\right)} \cdot \sqrt{2 \sin \theta} \\ & Z-i=e^{i\left(\frac{\theta}{2}+\frac{\pi}{4}\right)} \cdot\left[2 i \sin \left(\frac{\theta}{2}-\frac{\pi}{4}\right) \pm \sqrt{2 \sin \theta}\right]\end{aligned}$

$\begin{aligned} & |Z-i|=1 \cdot \sqrt{4 \sin ^2\left(\frac{\theta}{2}-\frac{\pi}{4}\right)+2 \sin \theta} \\ & =\sqrt{2\left(1-\cos \left(\theta-\frac{\pi}{2}\right)\right)+2 \sin \theta} \\ & =\sqrt{2(1-\sin \theta)+2 \sin \theta} \\ & =\sqrt{2}\end{aligned}$

$|Z-i|=|\alpha-i|=|\beta-i|$

$|\alpha-i|+|\beta-i|=2 \sqrt{2}$

Hence, the answer is $2 \sqrt{2}$.

Example 2: $\mathrm{z}=\frac{16}{1+i \sqrt{2}}$ , its Euler form is?

Solution:

We simplify z, and for that, we normalize the denominator

$\mathrm{z}=\frac{16}{1+\mathrm{i} \sqrt{3}} \cdot \frac{1-\mathrm{i} \sqrt{3}}{1-\mathrm{i} \sqrt{3}}=4(1-\mathrm{i} \sqrt{3})$

Now we see it lies in the 4th quadrant, so the argument is going to be -ve.

First we find r = |z| = 4·2=8
$
\theta=\arg (\mathrm{z})=\tan ^{-1}(-\sqrt{3})=\frac{-\pi}{3}
$
So euler form $=r e^{\mathrm{i} \theta}=8 \mathrm{e}^{-\frac{\pi}{3} \mathrm{i}}$

Hence, the answer is $8 e^{-\frac{\pi}{3}}$.

Example 3: If z is a non-real complex number, then the minimum value of $\frac{\operatorname{Im} z^5}{(\operatorname{Im} z)^5}$

Solution:

As we have learned

Polar Form of a Complex Number -

$z=r(\cos \theta+i \sin \theta)$

- wherein

r= modulus of z and $\theta$ is the argument of$\mathbf{Z}$

Euler's Form of a Complex Number -

$z=r e^{i \theta}$

- wherein

r denotes the modulus of z and $\theta$ denotes the argument of z .

$z=x+i y=r(\cos \theta+i \sin \theta)$

$=r e^{i \theta}$

So, $\operatorname{Im} z^5=\operatorname{Im}\left(r e^{i \theta}\right)^5$

$=\operatorname{Im}\left(r^5 e^{i \theta 5}\right)$

$=r^5 \sin 5 \theta$

$(\operatorname{Im} z)^5=(r \sin \theta)^5$

$=\left(r^5 \sin ^5 \theta\right)$

So, $\frac{\operatorname{Im} z^5}{(\operatorname{Im} z)^5}=\frac{\sin 5 \theta}{\sin ^5 \theta}$

for minimum value, differentiating w.r.t $\theta$

So, $\frac{\sin ^5 \theta \cdot 5 \cos \theta-5 \sin 5 \theta \sin ^4 \theta \cos \theta}{\sin ^{10} \theta}$

$\Rightarrow \sin \theta \cdot \cos 5 \theta-\sin 5 \theta \cos \theta=0$
$\Rightarrow \sin 4 \theta \cdot=0$
$4 \theta=n \pi$
$\theta=n \pi / 4$
for $n=1$

$
\frac{\sin 5 \theta}{\sin ^5 \theta}=\frac{-1 / \sqrt{2}}{(1 / \sqrt{2})^5}=-4
$
Hence, the answer is -4.

Example 4: If z is a complex number of unit modulus and argument $\theta$ ,then arg $\left(\frac{1+z}{1+\bar{z}}\right)$ equals:

Solution:

$|z|=1$

Arg (z)= $\theta$

So, $\frac{1+z}{1+\bar{z}}=\frac{1+\cos \theta+i \sin \theta}{1+\cos \theta-i \sin \theta}$

$\frac{2 \cos ^2 \theta / 2+2 i \sin \theta / 2 \cos \theta / 2}{2 \cos ^2 \theta / 2-2 i \sin \theta / 2 \cos \theta / 2}$

$=\frac{\cos \theta / 2+i \sin \theta / 2}{\cos \theta / 2-i \sin \theta / 2}$

$=\frac{e^{i \theta / 2}}{e^{-i \theta / 2}}$

$=e^{i \theta}$

Thus, arg$\left(\frac{1+z}{1+\bar{z}}\right)=\theta$

Hence, the answer is $\theta$.

Example 5: If $z$ and $w$ are two complex numbers such that $|z w|=1$ and $\arg (z)-\arg (w)=\frac{\pi}{2}$ then :

1) $z \bar{w}=i$

2) $z \bar{w}=\frac{-1+i}{\sqrt{2}}$

3) $\bar{z} w=-i$

4) $z \bar{w}=\frac{1-i}{\sqrt{2}}$

Solution

Euler's Form of a Complex Number -

$z=r e^{i \theta}$

- wherein

r denotes the modulus of $z$ and $\theta$ denotes the argument of $z$.

Polar Form of a Complex Number -

$z=r(\cos \theta+i \sin \theta)$

- wherein

$r=$ modulus of $z$ and $\theta$ is the argument of $z$

Now,

$|z w|=1$ and $\arg (z)-\arg (w)=\frac{\pi}{2}$

Let $|z|=r$ $\Rightarrow z=r e^{i \theta}$

$|\omega|=\frac{1}{r}$ $=>\omega=\frac{1}{r} e^{i \phi}$

$\arg (z)-\arg (w)=\frac{\pi}{2}$

$\theta-\phi=\frac{\pi}{2}$

$\theta=\frac{\pi}{2}+\phi$

$z \bar{\omega}=r e^{i \theta} \cdot \frac{1}{r} e^{-i \phi}$

$=r e^{i(\theta-\phi)}$

$\begin{aligned} & =r e^{i\left(\frac{\pi}{2}+\phi-\phi\right)} \\ & =r e^{i\left(\frac{\pi}{2}\right)} \\ & =\cos \left(\frac{\pi}{2}\right)+i \sin \left(\frac{\pi}{2}\right) \\ & =0+i .1 \\ & =i\end{aligned}$

Hence, the answer is the option (1).