Graphical Representation of Quadratic Equation

A quadratic graph depicts a U-shaped curve drawn for a quadratic function. In Mathematics, a parabola is one of the conic sections, which is formed by the intersection of a right circular cone by a plane surface. It is a symmetrical plane U-shaped curve. A parabola graph whose equation is in the form of $f(x)=a x^2+b x+c$ is the standard form of a parabola. The vertex of a parabola is the extreme point in it whereas the vertical line passing through the vertex is the axis of symmetry.

This Story also Contains

1. What is a Parabola Graph?
2. Standard Form of Parabola Equation
3. Vertex Form of Parabola Equation
4. Solved Examples Based on Graph of Quadratic Equations

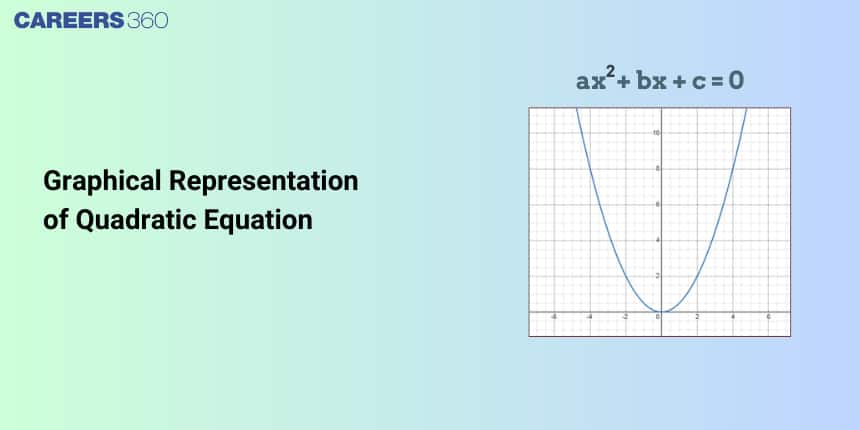
In this article, we will cover the concept of the graph of quadratic equations. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.

What is a Parabola Graph?

A parabola is a U-shaped curve that is drawn for a quadratic function, $\mathrm{f}(\mathrm{x})=a x^2+b x+c$. The graph of the parabola is downward (or opens down) when the value of $a$ is less than $0, a<0$. The graph of parabola is upward (or opens up) when the value of

$a$ is more than $0, a>0$. Hence, the direction of a parabola is determined by the sign of coefficient ' $a$ '.

Vertex

The vertex of parabola will represent the maximum and minimum point of parabola.

Axis of Symmetry

The axis of symmetry of parabola always passes through its vertex and is parallel to y-axis.

y-intercept

The point at which the parabola graph passes through the y-axis is called y-intercept. The parabola of quadratic function passes through an only a single point at the y-axis,

x-intercepts

The points at which the parabola graph passes through the x-axis, are called x-intercepts, which expresses the roots of quadratic function.

Standard Form of Parabola Equation

The equation of parabola can be expressed in two different ways, such as the standard form and the vertex form. The standard form of parabola equation is expressed as follows:

$
f(x)=y=a x^2+b x+c
$

The orientation of the parabola graph is determined using the "a" value.
If the value of $a$ is greater than $0(a>0)$, then the parabola graph is oriented towards the upward direction.
If the value of $a$ is less than $0(a<0)$, then the parabola graph opens downwards.
The axis of symmetry from the standard form of the parabola equation is given as:

$
x=\frac{-b}{2 a}
$

Vertex Form of Parabola Equation

The extreme point of a parabola, whether it is maximum or minimum, is called the vertex of the parabola. The parabola equation can also be represented using the vertex form.

Vertex Form of a Parabola:

$
f(x)=y=a(x-h)^2+k
$

Here, $(h, k)$ is the vertex of the parabola.

Similar to the standard form of the parabola equation, the orientation of the parabola in the vertex form is determined by the parameter " $a$ ".
- If the value of $a$ is positive $(a>0)$, the parabola opens upward.
- If the value of $a$ is negative $(a<0)$, the parabola opens downward.

How to graph a quadratic function ?

We have $y=f(x)=a x^2+b x+c$ where $a, b, c \in R$ and $a \neq d$
Expression $y=a x^2+b x+c=f(x)$ can be represented as

$
y=a\left(x^2+\frac{b}{a} x+\frac{c}{a}\right)
$

which on further simplification is converted in the form of

$
\begin{aligned}
& \Rightarrow y=a\left[\left(x+\frac{b}{2 a}\right)^2-\frac{D}{4 a^2}\right] \\
& \text { or }\left(y+\frac{D}{4 a}\right)=a\left(x+\frac{b}{2 a}\right)^2
\end{aligned}
$

Now, let $y+\frac{D}{4 a}=Y$ and $x+\frac{b}{2 a}=X$

$
\therefore \mathrm{Y}=\mathrm{aX}^2
$

The shape of the $y=f(x)$ will be parabolic
Vertex of the parabola will be $\left(\frac{-\mathrm{b}}{2 \mathrm{a}}, \frac{-\mathrm{D}}{4 \mathrm{a}}\right)$

$
\left[y+\frac{D}{4 a}=0 \Rightarrow y=-\frac{D}{4 a}\right]
$

If the parabola opens upward (when a > 0) then the y value of the vertex represents the least value of the equation, and if opens downward (when a < 0) then the y value of the vertex represents the greatest value of the parabola.

Both least and greatest values are attained at the x value of the vertex of the parabola

Hence the graph of any general quadratic equation will look like the below graph (given a>0)

In the general quadratic equation if $y=a x^2+b x+c=f(x)$ and if $a>0$
Then the parabola opens upward. As given below,

if a < 0 it opens downward. As given below,

Important points on Graphing Quadratic Functions

• The graph of the quadratic function is in the form of a parabola.
• The coefficient a in $f(x)=a(x-h)^2+k$ determines whether the graph of a quadratic function will open upwards or downwards.
• Graphing Quadratic Functions can be done using both general form and vertex form.

Recommended Video Based on Graph of Quadratic Equations

Solved Examples Based on Graph of Quadratic Equations

Example 1: $f(x)=2 x^2+a x+2$ if $f(x)=0$ has no real root then ' $a^{\prime}$ takes value lying in an interval
1) $(-5,5)$
2) $(-4,4)$
3) $(-6,6)$
4) $(-7,7)$

Solution:
As we learned in
Quadratic Expression Graph when $\mathrm{a}>0 \& \mathrm{D}<0$ -
No Real and Equal root of

$
\begin{aligned}
& f(x)=a x^2+b x+c \\
& \& D=b^2-4 a c \\
& \text { - wherein }
\end{aligned}
$

$\because f(x)=0$ has no real root, so $D<0$

$
\therefore a^2-16<0 \Rightarrow a \epsilon(-4,4)
$

$\therefore$ Option B
Example 2: If equations $a x^2+b x+c=0,(a, b, c \in R, a \neq 0)$ and $2 x^2+3 x+4=0$ Have a common root, then a:b:c equals :
1) $1: 2: 3$
2) $2: 3: 4$
3) $4: 3: 2$
4) $3: 2: 1$

Solution:
As we have learned
Quadratic Expression Graph when a $>0$ \& $<0$ -
No Real and Equal root of

$
\begin{aligned}
& f(x)=a x^2+b x+c \\
& \& D=b^2-4 a c
\end{aligned}
$

- wherein

Condition for both roots common -

$
\begin{aligned}
& \frac{a}{a^{\prime}}=\frac{b}{b^{\prime}}=\frac{c}{c^{\prime}} \\
& \text { - wherein } \\
& a x^2+b x+c=0_{\&} \\
& a^{\prime} x^2+b^{\prime} x+c^{\prime}=0
\end{aligned}
$

are the 2 equations

$
2 x^2+3 x+4=0 \text { has determinant }=9-32=-23<0
$

So, non-real roots which means both roots are common (as complex roots occur in conjugate )
So, a:b:c $=2: 3: 4 $

Example 3: The value of $\lambda$ such that the sum of the squares of the roots of the quadratic equation, $ x^{2} $
Solution:
Sum of Roots in Quadratic Equation -

$
\begin{aligned}
& a x^2+b x+c=0 \\
& a, b, c \in C
\end{aligned}
$

Product of Roots in Quadratic Equation -

$
\alpha \beta=\frac{c}{a}
$

- wherein
$\alpha$ and $\beta$ are roots of a quadratic equation:

$
\begin{aligned}
& a x^2+b x+c=0 \\
& a, b, c \in C
\end{aligned}
$

Quadratic Expression Graph when $a>0 \& \mathrm{D}<0$ -
No Real and Equal root of

$
\begin{aligned}
& f(x)=a x^2+b x+c \\
& \& D=b^2-4 a d \\
& \text { - wherein }
\end{aligned}
$

Given quadratic equation

$
x^2+(3-\lambda) x+2=\lambda
$

roots are $\alpha$ and $\beta$
from the concept

$
\begin{aligned}
\alpha+\beta & =\lambda-3 \text { and } \alpha \beta=2-\lambda \\
\alpha^2+\beta^2 & =(\alpha+\beta)^2-2 \alpha \beta \\
& =\lambda^2+9-6 \lambda-4+2 \lambda \\
& =\lambda^2-4 \lambda+5 \\
& =(\lambda-2)^2+1
\end{aligned}
$

least value when $\lambda=2$
Hence, the answer is 2 .
Example 4: Let $f(x)=x^2+2(a-1) x+(a+5)$, then the values of ' $a^{\prime}$ for which $f(x)=0$ doesn't have two real and distinct roots is
1) $(-1,4]$
2) $(-1,4)$
3) $(-1,4)$
4) $[-1,4]$

Solution:

Solution:
As we learned in
Quadratic Expression Graph when $\mathrm{a}>0$ \& $\mathrm{D}=0$ -
Real and Equal roots of

$
f(x)=a x^2+b x+c
$

\& $D=b^2-4 a c$
- wherein

$\because f(x)=0$ doesn't have real and distinct roots, so either it will have real and equal roots or imaginary roots.

$
\begin{aligned}
& \text { So } D \leq 0 \Rightarrow 4\left(a^2-2 a+1\right)-4(a+5) \leq 0 \\
& \Rightarrow(a-4)(a+1) \leq 0 \Rightarrow a \epsilon[-1,4]
\end{aligned}
$

Example 5: Let $f(x)=x^2+2(a-1) x+\left(a^2+1\right)$ then the values of ' $a$ ' for which $f(x)=0$ has real and equal roots is
Solution:
As we learned in
Quadratic Expression Graph when $a>0 \& D=0$ -
Real and Equal roots of

$
\begin{aligned}
& f(x)=a x^2+b x+c \\
& \& D=b^2-4 a c
\end{aligned}
$

- wherein

For $x^2+2(a-1) x+\left(a^2+1\right)=0$, to have real and equal roots, $D=0$

$
\begin{aligned}
& \Rightarrow 4\left(a^2-2 a+1\right)-4\left(a^2+1\right)=0 \\
& \Rightarrow a=0
\end{aligned}
$