Inverse Trigonometric Functions - Formulas, Graph, Domain & Range

Imagine you are standing in front of a tall tower and you need to find the height of the tower. In this case, the concept of trigonometry is used to determine the height of the tower using the angle you are standing at and the distance between you and the tower. Instead, imagine you standing in front of a tall tower for which the height is known, but you need to know the angle. In these cases, inverse trigonometric functions are used.

Inverse trigonometric functions are nothing but the reverse process of the trigonometric functions. For instance, Trigonometric functions are used to find the side lengths of a triangle while inverse trigonometric functions are used to determine the acute angle of the right triangle with the help of the side lengths.

Inverse trigonometric functions are the inverse functions of trigonometric functions. Inverse trigonometric functions have various applications across various domains like physics, engineering, computer graphics, robotics, economics, architecture and biology, etc.

This article is about the concept of Inverse Trigonometric Functions Class 12. Inverse trigonometric functions chapter is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, VITEEE, BCECE, and more.

Inverse Trigonometric Functions

Inverse trigonometric functions are the inverse functions of the trigonometric functions. The inverse trigonometric functions of the trigonometric functions $\sin, \cos, \tan, \csc, \sec, \cot$ are $\sin^{-1}, \cos^{-1}, \tan^{-1}, \csc^{-1}, \sec^{-1}, \cot^{-1}$.

Inverse trigonometric functins are the reverse process of the trigonometric functions. In other words, the domain of the inverse function is the range of the original function and vice versa.

For example, if $f(x)=\sin x$, then we would write $f^{-1}(x)=\sin ^{-1} x$. Be aware that $\sin ^{-1} x$ does not mean $1 / \sin x$. The following are the examples of inverse trigonometric functions:
1. $\sin (\pi / 6)=1 / 2$, then $\pi / 6=\sin ^{-1}(1 / 2)$
2. $\cos (\pi)=-1$, then $\pi=\cos ^{-1}(-1)$
3. $\tan (\pi / 4)=1$, then $(\pi / 4)=\tan ^{-1}(1)$

To make the inverse of trigonometric functions to be defined, the actual domain of trigonometric function must be restricted to make it a one-one function and its co-domain should be restricted to make it an onto function.

The domain of the sine function is $R$ and the range is $[-1,1]$. If we restrict its domain to $[-\pi / 2, \pi / 2]$ then it becomes one-one and if we restrict its co-domain to $[-1,1]$, then it becomes onto. So for this new domain and range, the inverse of our function $y=\sin (x)$ is defined. Domain for this inverse function $y=\sin ^{-1}(x)$ will be a range of $y=\sin (x):[-1,1]$ and its range will be equal to the domain of $y=\sin (x):[-\pi / 2, \pi / 2]$

Actually, the sine function can be restricted to any of the intervals $[-3 \pi / 2,-\pi / 2],[-\pi / 2, \pi / 2],[\pi / 2,3 \pi / 2]$ and so on. It becomes one-one in all the mentioned intervals and it is also onto (if the codomain is [-1,1]). We can, therefore, define the inverse of the sine function in each of these intervals. But by convention, we take the domain as $[-\pi / 2, \pi / 2]$, and this domain is called the Principal domain/ Principal value branch of $y=$ $\sin (x)$

So if $f:[-\pi / 2, \pi / 2] \rightarrow[-1,1]$ and $f(x)=\sin (x)$, then its inverse is
$f^{-1}:[-1,1] \rightarrow[-\pi / 2, \pi / 2]$ and $f^{-1}(x)=\sin ^{-1}(x)$
In a similar way, we could define the other trigonometric functions by restricting their domain and co-domains.

So, the range of the inverse trigonometric function is the restricted domain of the corresponding trigonometric function.

Inverse Trigonometric Functions are

1. Arcsine
The arcsine function is an inverse of the sine function denoted by $\sin ^{-1}$

2. Arccosine
The arccosine function is an inverse of the sine function denoted by $\cos ^{-1}$.

3. Arctangent
The arctangent function is an inverse of the tangent function denoted by $\tan ^{-1}$.

4. Arccotangent
Arccotangent function is an inverse of the cotangent function denoted by $\cot ^{-1}$.

5. Arcsecant
The arcsecant function is an inverse of the secant function denoted by $\sec^{-1}$.

6. Arccosecant
The arccosecant function is an inverse of the cosecant function denoted by $\csc^{-1}$.

Inverse Trigonometric Functions Class 12 Notes

Inverse trigonometric functions class 12 notes includes inverse trigonometric functions formulas, domain and range of inverse trigonometric functions, derivative of inverse trigonometric functions, integration of inverse trigonometric functions, graphs of inverse trigonometric functions and inverse trigonometric functions.

Domain and Range of Inverse Trigonometric Functions

The range and domain of inverse trigonometric functions,

Domain of Inverse Trigonometric Function

Domain is defined as a set of all possible values of $x$ for which$f(x)$ is true. The domain of an inverse function is equal to the range of the function.

Domain of $\sin ^{-1}(x)$ is $[-1,1]$ or $-1 \leq x \leq 1$
Domain of $\cos ^{-1}(x)=[-1,1]$
Domain of $\csc ^{-1}(x)=(-\infty,-1]$ or $[1,+\infty)$
Domain of $\sec ^{-1}(x)=(-\infty,-1]$ or $[1,+\infty)$
Domain of $\tan ^{-1}(\mathrm{x})=$ All Real Numbers
Domain of $\cot ^{-1}(x)=$ All Real Numbers

Range of Inverse Trigonometric Function

The range is defined as the set of all output values f(x) that are possible for $x$.

Range of $y=\sin ^{-1}(x)$ is,$-\pi / 2 \leq y \leq \pi / 2$
Range of $y=\cos ^{-1}(x)$ is $0 \leq y \leq \pi$
Range of $y=\csc ^{-1}(x)$ is $,-\pi / 2 \leq y \leq \pi / 2, y \neq 0$
Range of $y=\sec ^{-1}(x)$ is $0 \leq y \leq \pi, \quad y \neq \pi / 2$
Range of $y=\sec ^{-1}(x)$ is $0 \leq y \leq \pi, \quad y \neq \pi / 2$
Range of $y=\sec ^{-1}(x)$ is $0 \leq y \leq \pi, \quad y \neq \pi / 2$

Graph of Inverse Trigonometric Functions

The graphs of inverse trigonometric functions are

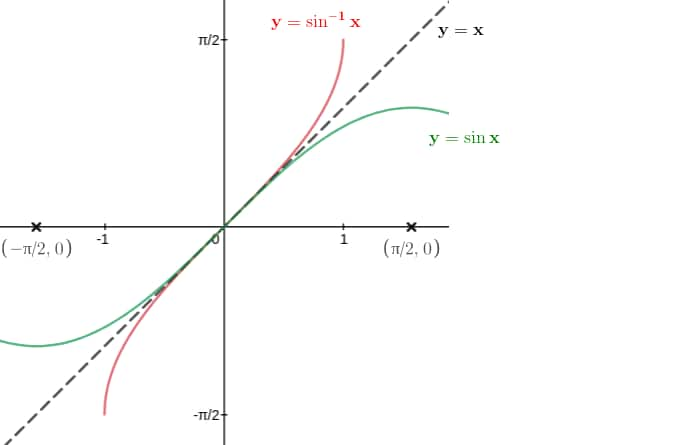
$y=\sin ^{-1}(x)$

$\sin ^{-1}(x)$ is the inverse of the trignometric function $\sin x$.

$\mathrm{y}=\sin \mathrm{x}, \mathrm{x} \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ and $\mathrm{y} \in[-1,1]$

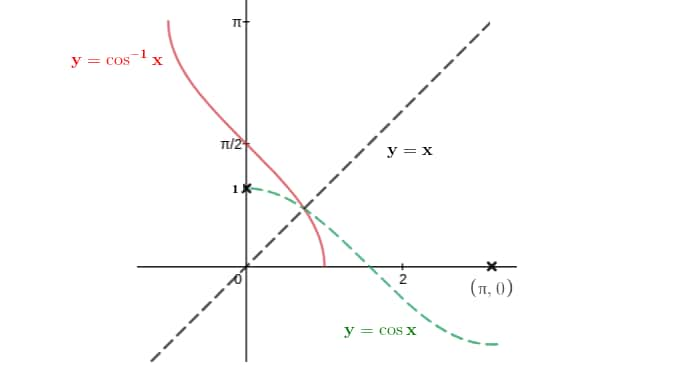
$y=\cos ^{-1}(x)$

$\cos ^{-1}(x)$ is the inverse of $\cos x$

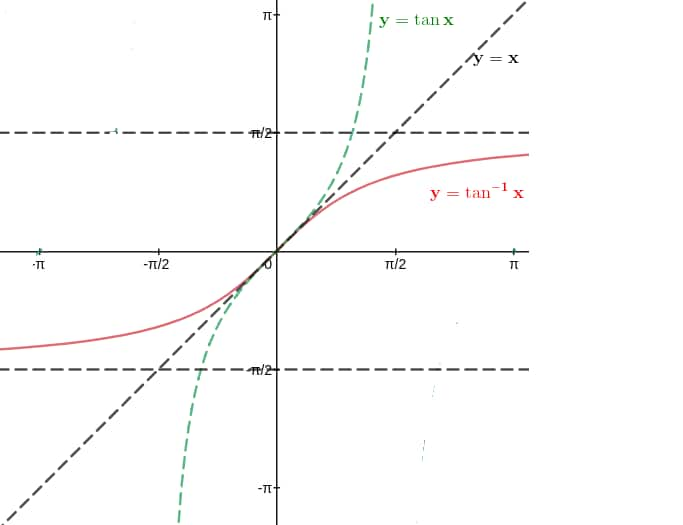
$y=\tan ^{-1}(x)$

$\tan ^{-1}(x)$ is the inverse of $\tan x$.

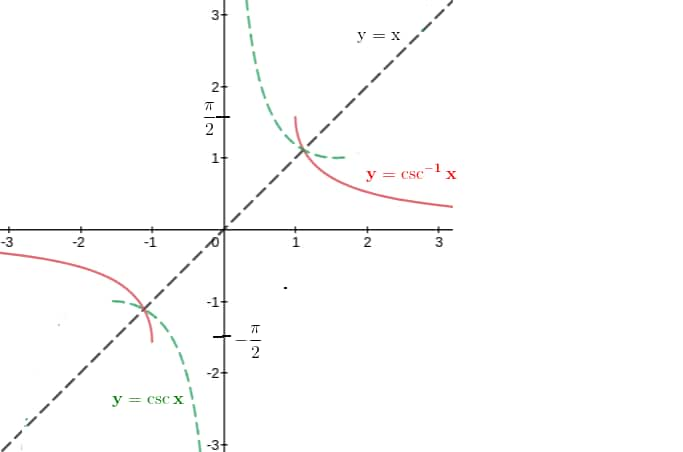
$y=\operatorname{cosec}^{-1}(x)$

$\operatorname{cosec}^{-1}(x)$ is the inverse of $\operatorname{cosec} x$.

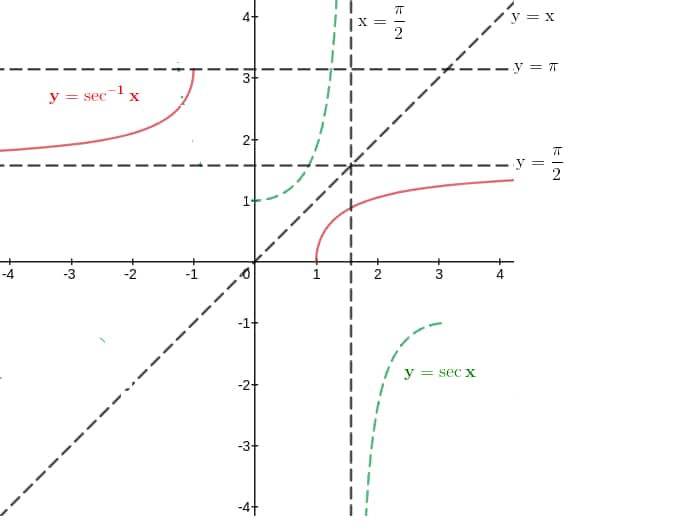
$y=\sec ^{-1}(x)$

$\sec ^{-1}(x)$ is the inverse of $\sec x$.

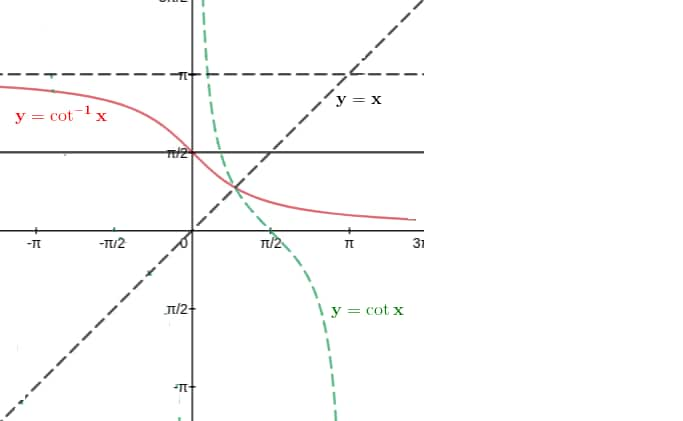
$y=\cot ^{-1}(x)$

$\cot ^{-1}(x)$ is the inverse of $\cot x$.

Inverse Trigonometric Functions Formulas

Inverse trigonometric functions formulas are,

Formulas for Negative Functions

$\sin ^{-1}(-x)=-\sin ^{-1}(x)$ for all $x \in[-1,1]$

$\tan ^{-1}(-x)=-\tan ^{-1}(x)$ for all $x \in R$ and

$\operatorname{cosec}^{-1}(-x)=-\operatorname{cosec}^{-1}(x)$ for all $x \in R-(-1,1)$

$\cos ^{-1}(-x)=\pi-\cos ^{-1}(x)$ for all $x \in[-1,1]$

$\sec ^{-1}(-x)=\pi-\sec ^{-1}(x)$ for all $x \in R-(-1,1)$

$\cot ^{-1}(-x)=\pi-\cot ^{-1}(x)$ for all $x \in R$

Formulas for Reciprocal Functions

$\sin ^{-1}\left(\frac{1}{\mathrm{x}}\right)=\csc ^{-1} \mathrm{x} \quad$ for all $\mathrm{x} \in(-\infty,-1] \cup[1, \infty)$

$\cos ^{-1}\left(\frac{1}{\mathrm{x}}\right)=\sec ^{-1} \mathrm{x} \quad$ for all $\mathrm{x} \in(-\infty,-1] \cup[1, \infty)$

$\tan ^{-1}\left(\frac{1}{\mathrm{x}}\right)=\left\{\begin{array}{cc}\cot ^{-1} x & \text { for } x>0 \\ -\pi+\cot ^{-1} x & \text { for } x<0\end{array}\right.$

Formulas for Complementary Functions

The complementary function pairs are, sine-cosine, tangent-cotangent, and secant-cosecant i.e. for a similar function the sum of these functions results in the right angle. The formulas for complemetary functions are

$\sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}$, for all $x \in[-1,1]$

$\tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}$, for all $x \in R$

$\sec ^{-1} x+\operatorname{cosec}^{-1} x=\frac{\pi}{2}$ for all $x \in(-\infty,-1] \cup[1, \infty)$

The sum and difference of trigonometry formulas convert the sum and difference of inverse trigonometric functions into single inverse trigonometric functions.

Sum of angles in terms of arctan

The formulas for the sum of anlges in terms of arctan are,

1. $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\left\{\begin{array}{cc}\tan ^{-1}\left(\frac{x+y}{1-x y}\right), & \text { If } \mathrm{x}>0, y>0, x y<1 \\ \pi+\tan ^{-1}\left(\frac{x+y}{1-x y}\right), & \text { If } \mathrm{x}>0, \mathrm{y}>0 \text { and } \mathrm{xy}>1 \\ -\pi+\tan ^{-1}\left(\frac{x+y}{1-x y}\right), & \text { If } \mathrm{x}<0, \mathrm{y}<0 \text { and } \mathrm{xy}>1\end{array}\right.$

Difference of angles in terms of arctan

The formulas for the difference of anlges in terms of arctan are,

1. $\tan ^{-1} \mathrm{x}-\tan ^{-1} \mathrm{y}=\left\{\begin{array}{cc}\tan ^{-1}\left(\frac{x-y}{1+x y}\right), & \text { If } x y>-1 \\ \pi+\tan ^{-1}\left(\frac{x-y}{1+x y}\right), & \text { If } \mathrm{x}>0, \mathrm{y}<0 \text { and } \mathrm{xy}<-1 \\ -\pi+\tan ^{-1}\left(\frac{x-y}{1+x y}\right), & \text { If } \mathrm{x}<0, \mathrm{y}>0 \text { and } \mathrm{xy}<-1\end{array}\right.$

Sum and difference of angles in terms of arcsin

We have the following formulas for the sum of angles when angles are in terms of arcsin

1. $\sin ^{-1} \mathrm{x}+\sin ^{-1} \mathrm{y}= \begin{cases}\sin ^{-1}\left\{x \sqrt{1-y^2}+y \sqrt{1-x^2}\right\} & \text { if }-1 \leq x, y \leq 1 \text { and } x^2+y^2 \leq 1 \\ \pi-\sin ^{-1}\left\{x \sqrt{1-y^2}+y \sqrt{1-x^2}\right\} & \text { or, if } x y<0 \text { and } x^2+y^2>1 \\ & \text { if } 0<x, y \leq 1 \text { and } x^2+y^2>1 \\ -\pi-\sin ^{-1}\left\{x \sqrt{1-y^2}+y \sqrt{1-x^2}\right\} & \text { if }-1 \leq x, y<0 \text { and } x^2+y^2>1\end{cases}$

We have the following formulas for the difference of angles when angles are in terms of arcsin

2. $\sin ^{-1} \mathrm{x}-\sin ^{-1} \mathrm{y}= \begin{cases}\sin ^{-1}\left\{x \sqrt{1-y^2}-y \sqrt{1-x^2}\right\} & \text { if }-1 \leq x, y \leq 1 \text { and } x^2+y^2 \leq 1 \\ \pi-\sin ^{-1}\left\{x \sqrt{1-y^2}+y \sqrt{1-x^2}\right\} & \text { or, if } x y>0 \text { and } x^2+y^2>1 \\ & \text { if } 0<x \leq 1 ;-1 \leq y<0 \text { and } x^2+y^2>1 \\ -\pi-\sin ^{-1}\left\{x \sqrt{1-y^2}+y \sqrt{1-x^2}\right\} & \text { if }-1 \leq x<0 ; 0<y \leq 1 \text { and } x^2+y^2>1\end{cases}$

Sum and difference of angles in terms of arccos

We have the following formulas for the sum and difference of angles when angles are in terms of arc

1. $\cos ^{-1} x+\cos ^{-1} y=\cos ^{-1}\left\{x y-\sqrt{1-x^2} \sqrt{1-y^2}\right\} \quad$ if $0<x, y \leq 1$
2. $\cos ^{-1} x-\cos ^{-1} y= \begin{cases}\cos ^{-1}\left\{x y+\sqrt{1-x^2} \sqrt{1-y^2}\right\} & \text { if } 0 \leq x, y \leq 1 \text { and } x \leq y \\ -\cos ^{-1}\left\{x y+\sqrt{1-x^2} \sqrt{1-y^2}\right\} & \text { if } 0<x, y \leq 1 \text { and } x>y\end{cases}$

Multiple angles in terms of arcsin

1. Double of Inverse Trigonometric Function Formulas

$2 \sin ^{-1} \mathrm{x}=\left\{\begin{array}{cc}\sin ^{-1}\left(2 x \sqrt{1-x^2}\right), & \frac{1}{\sqrt{2}} \leq x \leq \frac{1}{\sqrt{2}} \\ \pi-\sin ^{-1}\left(2 x \sqrt{1-x^2}\right), & x>\frac{1}{\sqrt{2}} \\ -\pi-\sin ^{-1}\left(2 x \sqrt{1-x^2}\right), & x<-\frac{1}{\sqrt{2}}\end{array}\right.$

2. Triple of Inverse Trigonometric Function Formulas

$3 \sin ^{-1} \mathrm{x}=\left\{\begin{array}{cc}\sin ^{-1}\left(3 x-4 x^3\right), & -\frac{1}{2} \leq x \leq \frac{1}{2} \\ \pi-\sin ^{-1}\left(3 x-4 x^3\right), & x>\frac{1}{2} \\ -\pi-\sin ^{-1}\left(3 x-4 x^3\right) & x:-\frac{1}{2}\end{array}\right.$

Multiple angles in terms of arccos

1. Double of Inverse Trigonometric Function Formulas

$2 \cos ^{-1} \mathrm{x}=\left\{\begin{array}{cc}\cos ^{-1}\left(2 x^2-1\right), & \text { if } 0 \leq x \leq 1 \\ 2 \pi-\cos ^{-1}\left(2 x^2-1\right), & \text { if }-1 \leq x \leq 0\end{array}\right.$
2. Triple of Inverse Trigonometric Function Formulas

$3 \cos ^{-1} \mathrm{x}=\left\{\begin{array}{cc}\cos ^{-1}\left(4 x^3-3 x\right), & \text { if } \frac{1}{2} \leq x \leq 1 \\ 2 \pi-\cos ^{-1}\left(4 x^3-3 x\right), & \text { if }-\frac{1}{2} \leq x \leq \frac{1}{2} \\ 2 \pi+\cos ^{-1}\left(4 x^3-3 x\right), & \text { if }-1 \leq x \leq-\frac{1}{1}\end{array}\right.$

Multiple angles in terms of arctan and arcsin

The multiple-angle formula of arctan in terms of arcsin is given by

$2 \tan ^{-1} \mathrm{x}=\left\{\begin{array}{cc}\sin ^{-1}\left(\frac{2 x}{1+x^2}\right), & \text { if }-1 \leq x \leq 1 \\ \pi-\sin ^{-1}\left(\frac{2 x}{1+x^2}\right), & \text { if } x>1 \\ -\pi-\sin ^{-1}\left(\frac{2 x}{1+x^2}\right), & \text { if } x<-1\end{array}\right.$

Multiple angles in terms of arctan and arccos

The multiple angle formula of arctan in terms of arccos is given by

$2 \tan ^{-1} \mathrm{x}=\left\{\begin{array}{cc}\cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right), & \text { if } 0 \leq x<\infty \\ -\cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right), & \text { if }-\infty<x \leq 0\end{array}\right.$

Differentiation of Inverse Trigonometric Functions

The derivative of inverse trigonometic fucnctions are

$\begin{aligned} & \frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^2}}, x \neq \pm 1 \\ & \frac{d}{d x}\left(\cos ^{-1} x\right)=\frac{-1}{\sqrt{1-x^2}}, x \neq \pm 1 \\ & \frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{1+x^2} \\ & \frac{d}{d x}\left(\cot ^{-1} x\right)-\frac{-1}{1+x^2} \\ & \frac{d}{d x}\left(\sec ^{-2} x\right)=\frac{1}{|x| \sqrt{x^2-1}}, x \neq \pm 1.0 \\ & \frac{d}{d x}\left(\csc ^{-1} x\right)=\frac{-1}{|x| \sqrt{x^2-1}}, x \neq \pm 1.0\end{aligned}$

Integration of Inverse Trigonometric Functions

The integration of inverse trigonometric functions are

$\begin{aligned} & \int \sin ^{-1} x d x=x \sin ^{-1} x+\sqrt{1-x^2}+C \\ & \int \cos ^{-1} x d x=x \cos ^{-1} x-\sqrt{1-x^2}+C \\ & \int \tan ^{-1} x d x=x \tan ^{-1} x-\frac{1}{2} \ln \left|1+x^2\right|+C \\ & \int \csc ^{-1} x d x=x \csc ^{-1} x+\ln \left|x+\sqrt{x^2-1}\right|+C \\ & \int \sec ^{-1} x d x=x \sec ^{-1} x-\ln \left|x+\sqrt{x^2-1}\right|+C \\ & \int \cot ^{-1} x d x=x \cot ^{-1} x+\frac{1}{2} \ln \left|1+x^2\right|+C\end{aligned}$

Inverse Trigonometric Functions Table

The inverse trigonometric functions table consist of the domain and range of the inverse trigonometric functions.

\begin{array}{|l|l|l|}
\hline \text { Function } & \text { Domain } & \text { Range } \\
\hline y=\sin ^{-1} x & {[-1,1]} & {[-\pi / 2, \pi / 2]} \\
\hline y=\cos ^{-1} x & {[-1,1]} & {[0, \pi]} \\
\hline y=\operatorname{cosec}^{-1} x & R-(-1,1) & {[-\pi / 2, \pi / 2]-\{0\}} \\
\hline y=\sec ^{-1} x & R-(-1,1) & {[0, \pi]-\{\pi / 2\}} \\
\hline y=\tan ^{-1} x & R & (-\pi / 2, \pi / 2) \\
\hline y=\cot ^{-1} x & R & (0, \pi) \\
\hline
\end{array}

List of Topics According to NCERT/JEE MAIN

Importance of Inverse Trigonometric Functions Class 12

Inverse Trigonometric Functions have a significant weighting in the IIT JEE test, which is a national level exam for 12th grade students that aids in admission to the country's top engineering universities. It is one of the most difficult exams in the country, and it has a significant impact on students' futures. When it comes to math, the significance of these chapters cannot be overstated due to their great weightage. You may begin and continue your studies with the standard books and these revision notes, which will ensure that you do not miss any crucial ideas and can be used to revise before any test or actual examination.

How to Study Inverse Trigonometric Functions Class 12?

Start preparing by understanding and practicing to find the table of the inverse trigonometric functions. Try to be clear on concepts inverse trigonometric formula, differntiation and integration of trigonometric functions. Practice many problems from each topic for better understanding.

If you are preparing for competitive exams then solve as many problems as you can. Do not jump on the solution right away. Remember if your basics are clear you should be able to solve any question on this topic.

NCERT Notes Subject wise link:

• NCERT Notes for class 12 Physics.
• NCERT Notes for class 12 Chemistry.
• NCERT Notes for class 12 Mathematics.
• NCERT Notes for class 12 Biology

Important Books for Inverse Trigonometric Functions

Start from NCERT Books, the illustration is simple and lucid. You should be able to understand most of the things. Solve all problems (including miscellaneous problem) of NCERT. If you do this, your basic level of preparation will be completed.

Then you can refer to the book Trigonometry by SL Loney. Inverse Trigonometric Functions are explained very well in these books and there are an ample amount of questions with crystal clear concepts. Choice of reference book depends on person to person, find the book that best suits you the best, depending on how well you are clear with the concepts and the difficulty of the questions you require.

NCERT Solutions Subject wise link:

• NCERT solutions for class 12 Physics.
• NCERT solutions for class 12 Chemistry.
• NCERT solutions for class 12 Mathematics.
• NCERT solutions for class 12 Biology.

NCERT Exemplar Solutions Subject wise link:

• NCERT exemplar solutions for class 12 Physics.
• NCERT exemplar solutions for class 12 Chemistry.
• NCERT exemplar solutions for class 12 Mathematics.
• NCERT exemplar solutions for class 12 Biology.