Left-Hand and Right-Hand Limits: Definition, Formula, Examples

Limits are a fundamental concept in calculus that allows us to understand how functions behave as their inputs approach certain values. Limits are essential for defining derivatives and the related definite integrals. They help us analyze how functions behave locally around specific points of interest. This concept is essential for analyzing continuity, rates of change, and many other aspects of mathematical and real-world problems. Limits form the basis for defining derivatives and integrals, making them indispensable tools in calculus and beyond.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Left-Hand Limits and Right-Hand Limits
2. Solved Examples Based on Left-Hand Limits and Right-Hand Limits
3. Summary

In this article, we will cover the concept of Left Hand Limits And Right Hand Limits. This topic falls under the broader category of Calculus, which is a crucial chapter in Class 11 Mathematics. It is essential for board exams and competitive exams like the Joint Entrance Examination (JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, and BCECE. From 2013 to 2023, a total of seven questions were asked on JEE Main from this topic that is two in 2019, three in 2020, and two in 2022.

Left-Hand Limits and Right-Hand Limits

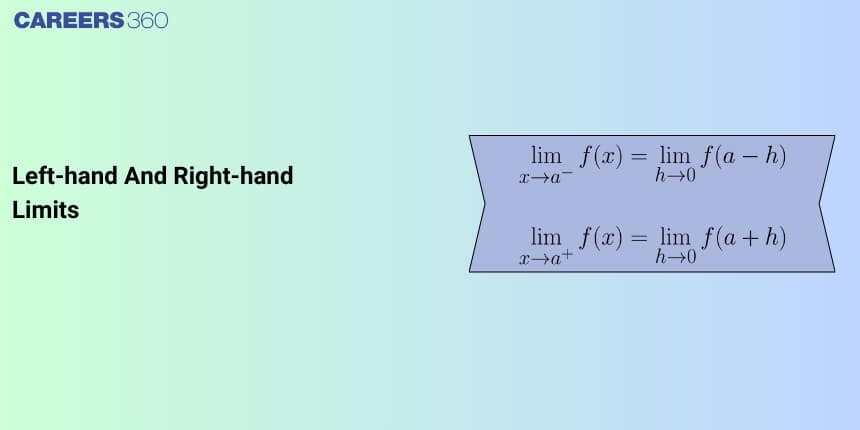
Left-Hand Limit $\lim\limits_{x \rightarrow a^{-}} f(x)$: The limit of $f(x)$ as $x$ approaches $c$ from the left - that is, through numbers smaller than $c$.
$\lim\limits _{x \rightarrow a^{+}} f(x)$ The limit of $f(x)$ as $x$ approaches $c$ from the right - that is, through numbers bigger than $c$.
Continuing from the previous concept, we can approach the input of a function from either side of a value-from the left or the right.
we had our function

$
\begin{aligned}
& f(x)=\frac{(x+1)(x-7))}{(x-7)}, x \neq 7 \\
& f(x)=x+1, x \neq 7
\end{aligned}
$

now, let us observe the values of $f(x)$ nearby $x=7$.

$\lim\limits _{x \rightarrow 7^{-}} f(x)=8$

Approaching $$7 "from the left" means that the values of input are just less than $7$. And if for such values of $x$, the values of $f(x)$ are close to $L$, then $L$ is called the left-hand limit of function at $x=7$. For this function, $8$ is the left-hand limit of the function $f(x)$ at $x=7$.

Approaching $7$ "from the right" means that the values of input are just larger than $7$. And if for such values of $x$, the values of $f(x)$ are close to $R$, then $R$ is called the right-hand limit of function at $x=7$. For this function, $8$ is the right-hand limit of the function $f(x)$ at $x=7$.

To indicate the left-hand limit, we write $\lim\limits _{x \rightarrow 7^{-}} f(x)=8$.
$7^{-}$ indicates the values that are less than $7$ and are infinitesimally close to $7$

To indicate the right-hand limit, we write $\lim\limits _{x \rightarrow 7^{+}} f(x)=8$.
$7^{+}$ indicates the values that are greater than $7$ and are infinitesimally close to $7$

The left-hand and right-hand limits are the same for this function.

( It denotes that if we can redefine the function, it is possible to define the value of the function at $x=7$ as $f(7)=8$. This is the scenario we will be observing the chapter again and again where, we define it that if $\mathrm{LHL}=$ RHL at a point $x=a$, then Limit of function at the point can be defined)

The left-hand limit of a function f(x) as x approaches a from the left is denoted by $\lim\limits _{x \rightarrow a^{-}} f(x)=L H L$

The right-hand limit of a function f(x) as x approaches a from the right is denoted by $\lim\limits _{x \rightarrow a^{+}} f(x)=R H L$

Now consider a function, $f(x)=\frac{|x|}{x}$
Let's check the behavior of $f(x)$ in the neighborhood of $x=0$

$
\mathrm{LHL}=\lim\limits _{\mathrm{x} \rightarrow 0^{-}} \frac{|\mathrm{x}|}{\mathrm{x}}
$

As $x$ is just less than 0 , we can replace it by $(0-h)$, where $h$ is positive and very close to 0

$
=\lim\limits _{\mathrm{h} \rightarrow 0^{+}} \frac{0-\mathrm{h} \mid}{0-\mathrm{h}}
$

So, we have

$
\begin{aligned}
& =\lim\limits _{h \rightarrow 0^{+}} \frac{|-h|}{-h} \\
& =\lim\limits _{h \rightarrow 0^{+}} \frac{h}{-h} \\
& =-1
\end{aligned}
$
$
\begin{aligned}
\mathrm{RHL} & =\lim\limits _{\mathrm{x} \rightarrow 0^{+}} \frac{|x|}{\mathrm{x}} \\
& =\lim\limits _{\mathrm{h} \rightarrow 0^{+}} \frac{|0+\mathrm{h}|}{0+\mathrm{h}} \\
& =\lim\limits _{\mathrm{h} \rightarrow \mathrm{0}^{+}} \frac{\mathrm{h}}{\mathrm{h}}=1
\end{aligned}
$
Here, we have RHL $\neq$ LHL

Existence of a limit of a function

From the above example, we can define the existence of limit

The limit of a function $f(x)$ at $x=a$ exists if $\lim\limits _{x \rightarrow a^{-}} f(x)=\lim\limits _{x \rightarrow a^{-}} f(x)$

i.e., $L H L=R H L$ at $x=a$

Also, notice that the limit of a function can exist even when $f(x)$ is not defined at $x=a$.

Recommended Video Based on Left-Hand and Right-Hand Limits

Solved Examples Based on Left-Hand Limits and Right-Hand Limits

Example 1: Let $[x]$ denote the greatest integer less than or equal to $x$. Then $x \rightarrow 0 \left\lvert\, \lim\limits _{x \rightarrow 0} \frac{\tan \left(\pi \sin ^2 x\right)+(|x|-\sin (x[x]))^2}{x^2}\right.$ [JEE Mains 2019]
1) equals $\pi+1$
2) equals $0$
3) does not exist
4) equals $\pi$

Solution:
Evaluation of Trigonometric limit -

$
\begin{aligned}
& \lim\limits _{x \rightarrow a} \frac{\sin (x-a)}{x-a}=1 \\
& \lim\limits _{x \rightarrow a} \frac{\tan (x-a)}{x-a}=1
\end{aligned}
$

put $x=a+h$ where $h \rightarrow 0$
Then it comes

$
\begin{aligned}
& \lim\limits _{h \rightarrow 0} \frac{\sin h}{h}=\lim\limits _{h \rightarrow 0} \frac{\tanh }{h}=1 \\
& \therefore \lim\limits _{x \rightarrow 0} \frac{\sin x}{x}=1 \text { and } \\
& \therefore \quad \lim\limits _{x \rightarrow 0} \frac{\tan x}{x}=1
\end{aligned}
$

Right hand limit -

The right hand limit of $f(x)$ as ' $x$ ' tends to 'a' exists and is equal to $l_1$, if as '$x$' approaches '$a$' through values greater than '$a$'.

so $\lim\limits _{x \rightarrow a^{+}} f(x)=l_1$

wherein

$\mathrm{a}^{+}$means $\mathrm{a}+\mathrm{h} \space $&$ \mathrm{~h} \rightarrow 0$. Therefore $\mathrm{f}(\mathrm{a}+\mathrm{h})$.

Left-hand Limit -

The left-hand limit of $f(x)$ as ' $x$ ' tends to '$a$' exists and is equal to $l_2$, if as 'x' approaches '$a$' through values less than '$a$'.

$
\lim\limits _{x \rightarrow a^{-}} f(x)=l_2
$
Where $\mathrm{a}^{-}$means ( $\mathrm{a}-\mathrm{h}$ ) $h \rightarrow 0$. Therefore, $\mathrm{f}(\mathrm{a}-\mathrm{h})$.

$
\begin{aligned}
& \lim\limits _{x \rightarrow 0} \frac{\tan \left(\pi \sin ^2 x\right)+(|x|-\sin (x[x]))^2}{x^2} \\
& =\lim\limits _{x \rightarrow 0}\left[\frac{\tan \left(x \sin ^2 x\right)}{x \sin ^2 x} \times \simeq\left(\frac{\sin x}{x}\right)^2+\frac{x^2}{x^2}-\frac{2|x| \sin (x[x])}{x^2}+\frac{\sin ^2(x[x])}{x^2}\right]
\end{aligned}
$
RHS, $\lim\limits x \rightarrow 0+, \quad|x|=x$ and $[x]=0$
So, RHS $=(\pi+1)$
LHS, $\lim\limits x \rightarrow 0-,|x|=-x$ and $[x]=-1$
So, LHS $=(\pi+1-2+1)=\pi$

Hence limit does not exist

Hence, the answer is the option 3.

Example 2: Let $f: R \rightarrow P$ defined as $f(x)=\left\{\begin{array}{c}x^5 \sin \left(\frac{1}{x}+5 x^2\right), x<0 \\ 0, x=0 \\ x^5 \cos \left(\frac{1}{x}+\lambda z^2, x<0\right)\end{array}\right.$ The value of $\lambda$ for which $f^{\prime \prime}(x)$ exists is: [JEE Mains 2020]

1) $2$

2) $3$

3) $5$

4) $6$

Solution:
L.H.L $=$ R.H.L.

$
\begin{aligned}
& 2 \lambda=10 \\
& \lambda=5
\end{aligned}
$

Hence, the answer is option (3).

$
\begin{aligned}
& f^{\prime}(x)=\left\{\begin{array}{c}
5 x^4 \sin \left(\frac{1}{x}\right)-x^3 \cos \left(\frac{1}{x}\right)+10 x, x<0 \\
0, \quad x=0 \\
5 x^4 \cos \left(\frac{1}{x}\right)+x^3 \sin \left(\frac{1}{x}\right)+2 \lambda, x>0
\end{array}\right. \\
& f^{\prime \prime}(x)=\left\{\begin{array}{c}
\text { term having } \mathrm{x} \text { in muliplication }+10, x<0 \\
0, \quad x=0 \\
\text { term having } \mathrm{x} \text { in muliplication }+2 \lambda, x>0
\end{array}\right.
\end{aligned}
$

L.H.L = R.H.L.

$\begin{aligned} & 2 \lambda=10 \\ & \lambda=5\end{aligned}$

Hence, the answer is option (3).

Example 3: Let [t] denote the greatest integer. If for some $\lambda \epsilon R-[0,1]_{x \rightarrow 0} \lim\limits _{x \rightarrow 0}\left|\frac{1-x+|x|}{\lambda-x+[x]}\right|=L$, then L is equal to: [JEE Mains 2020]

1) $12$

2) $2$

3) $\frac{1}{2}$

4) $0$

Solution:

$
\begin{aligned}
& \lim\limits _{x \rightarrow 0}\left|\frac{1-x+|x|}{\lambda-x+\mid x]}\right|=L \\
& L H L=\lim\limits _{x \rightarrow 0}\left|\frac{1-2 x}{\lambda-x-1}\right|=\frac{1}{|\lambda-1|} \\
& R H L=\lim\limits _{x \rightarrow 0}\left|\frac{1}{\lambda-x-0}\right|=\frac{1}{|\lambda|} \\
& \therefore \frac{1}{|\lambda-1|}=\frac{1}{|\lambda|} \Rightarrow \lambda=\frac{1}{2} \\
& \therefore L=2
\end{aligned}
$
Hence, the answer is the option 1.

Example 4. ${\lim\limits _{x \rightarrow a} \frac{(a+2 x)^{1 / 3}-(3 x)^{1 / 3}}{(3 a+x)^{1 / 3}-(4 x)^{1 / 3}}(a \neq 0)}$ is equal to?
[JEE Mains 2020]
1) $\left(\frac{2}{3}\right)^{\frac{4}{3}}$
2) $\left(\frac{2}{3}\right)\left(\frac{2}{9}\right)^{\frac{1}{3}}$
3) $\left(\frac{2}{9}\right)^{\frac{4}{3}}$
4) $\left(\frac{2}{9}\right)\left(\frac{2}{3}\right)^{\frac{1}{3}}$

Solution:

$
\begin{aligned}
L & =\lim\limits _{h \rightarrow 0} \frac{(a+2(a+h))^{1 / 3}-(3(a+h))^{1 / 3}}{(3 a+a+h)^{1 / 3}-(4(a+h))^{1 / 3}} \\
& =\lim\limits _{h \rightarrow 0} \frac{(3 a)^{1 / 3}\left(1+\frac{2 h}{3 a}\right)^{1 / 3}-(3 a)^{1 / 3}\left(1+\frac{h}{a}\right)^{1 / 3}}{(4 a)^{1 / 3}\left(1+\frac{h}{4 a}\right)^{1 / 3}-(4 a)^{1 / 3}\left(1+\frac{h}{a}\right)^{1 / 3}} \\
& =\lim\limits _{h \rightarrow 0}\left(\frac{3^{1 / 3}}{4^{1 / 3}}\right)\left[\frac{\left(1+\frac{2 h}{9 a}\right)-\left(1+\frac{h}{3 a}\right)}{\left(1+\frac{h}{12 a}\right)-\left(1+\frac{h}{3 a}\right)}\right] \\
& =\left(\frac{3}{4}\right)^{1 / 3} \frac{\left(\frac{2}{9}-\frac{1}{3}\right)}{\left(\frac{1}{12}-\frac{1}{3}\right)}=\left(\frac{3}{4}\right)^{1 / 3}\left(\frac{8-12}{3-12}\right) \\
& =\left(\frac{3}{4}\right)^{1 / 3}\left(\frac{-4}{-9}\right)=\frac{4^{1-\frac{1}{3}}}{3^{2-\frac{1}{3}}}=\frac{4^{2 / 3}}{3^{5 / 3}}
\end{aligned}
$
$
L=\frac{(8 \times 2)^{1 / 3}}{(27 \times 9)^{1 / 3}}=\frac{2}{3}\left(\frac{2}{9}\right)^{1 / 3}
$

Hence, the answer is the option 2.

Example 5:Let $[\mathrm{t}]$ denote the greatest integer $\leq \mathrm{t}$ and t denote the fractional part of t . The integral value of $\alpha$ for which the left-hand limit of the function $\mathrm{f}(\mathrm{x})=[1+\mathrm{x}]+\frac{\alpha^{2[\mathrm{x}]+\{\mathrm{x}\}}+[\mathrm{x}]-1}{2[\mathrm{x}]+\{\mathrm{x}\}} \mathrm{x}=0$ is equal to $\alpha-\frac{4}{3}$, is [JEE Mains 2022]
1) $3$
2) $4$
3) $6$
4) $0$

Solution

$
\lim\limits _{x \rightarrow 0^{-}}[x]=-1, \lim\limits _{x \rightarrow 0^{-}}\{x\}=1
$
So $\lim\limits _{x \rightarrow 0^{-}} f(x)$

$
\begin{aligned}
& =\lim\limits _{x \rightarrow-}\left(1+[x]+\frac{\alpha^{2[x]+\{x\}}+[x]-1}{2[x]+\{x\}}\right)=\alpha-\frac{4}{3} \\
& \Rightarrow \quad 1-1+\frac{\alpha^{2(-1)+1}+(-1)-1}{2(-1)+1}=\alpha-\frac{4}{3} \\
& \Rightarrow \quad \frac{\frac{1}{\alpha}-2}{-1}=\alpha-\frac{4}{3} \Rightarrow-\frac{1}{2}+2=\alpha-\frac{4}{3} \\
& \Rightarrow \alpha+\frac{1}{\alpha}=\frac{10}{3} \Rightarrow 3 \alpha^2-10 \alpha+3=0 \\
& \Rightarrow \alpha=3 \text { OR } \alpha=1 / 3
\end{aligned}
$
Since $\alpha=$ integer,

$
\alpha=3
$
Hence, the answer is $3$

Summary