Line of Intersection of Two Planes

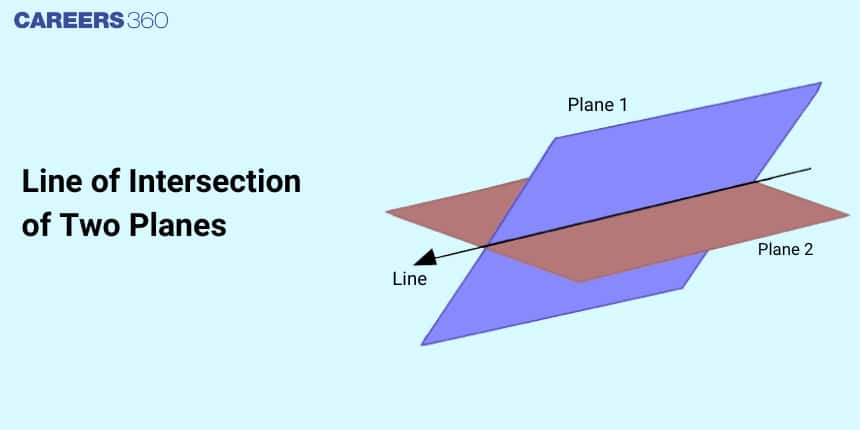
The intersection of two non-parallel planes always forms a line, for example in three three-dimensional coordinate systems, the intersection of the $X Y$ plane with the $X Z$ plane forms $X$-axis. The angle between a line and a plane is the complement of the angle between the line and normal to the plane. In real life, we use the Intersection of two planes for connecting walls and binding papers.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is the Line of Intersection of Two Plane?
2. Vector Equation of Line of Intersection
3. What is the Angle Between a Line and a Plane?
4. Equation of Angle Between a Line and a Plane in Vector Form
5. Equation of Angle Between a Line and a Plane in Cartesian Form
6. The intersection of a line and a plane
7. Condition for a Line to be Parallel to a Plane
8. Condition for a Line to Lie in the Plane
9. Summary

In this article, we will cover the concept of the Line of Intersection of Two Plane and the Angle Between a Line and a Plane. This topic falls under the broader category of Three Dimensional Geometry, which is a crucial chapter in Class 12 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of nineteen questions have been asked on this topic in JEE Main from 2013 to 2023 including seven in 2019, nine in 2021, four in 2022, and ten in 2023.

What is the Line of Intersection of Two Plane?

Intersecting planes are planes that are not parallel, and they always intersect in a line.

What is the equation of a line when the $Y Z$ plane and $X Z$ plane intersect?

Let the equation of two non-parallel planes be $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_1=d_1$ and $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_2=d_2$

Now, the line of intersection of planes is perpendicular to $\overrightarrow{\mathbf{n}}_1$ and $\overrightarrow{\mathbf{n}}_2$. Therefore, the line of intersection is parallel to vector $\overrightarrow{\mathbf{n}}_1 \times \overrightarrow{\mathbf{n}}_2$.

Vector Equation of Line of Intersection

The vector equation for the line of intersection is given by

$
\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_0+t \overrightarrow{\mathbf{v}}
$
Where, $\overrightarrow{\mathbf{v}}$ is the vector result of the normal vector of the two planes.
To find the line of intersection of planes $a_1 x+b_1 y+c_1 z=d_1$ and $a_2 x+b_2 y+c_2 z=d_2$, then first find any point on the line by putting $z=0$ (say), then we can find corresponding values of x and y be solving equations $\mathrm{a}_1 \mathrm{x}+\mathrm{b}_1 \mathrm{y}+\mathrm{c}_1 \mathrm{z}=\mathrm{d}_1$ and $\mathrm{a}_2 \mathrm{x}+\mathrm{b}_2 \mathrm{y}+\mathrm{c}_2 \mathrm{z}=\mathrm{d}_2$

Thus, by fixing the value of $z=\lambda$ we can find the corresponding value of $x$ and $y$ in terms of $\lambda$. After getting $x, y$, and $z$ in terms of $\lambda$ we can find the equation of line in symmetric form.

Illustration

The line of intersection of two given plane $P_1:-3 x+2 y-3 z-1=0$ and $P_2: 2 x-y-4 z+2=0$ is

Let $z=\lambda$
Then,

$
-3 x+2 y=1+3 \lambda
$

and

$
2 x-y=-2+4 \lambda
$
Solve these two equations, $x=-3+11 \lambda$ and $y=-4+18 \lambda$
The equation of the line is

$
\frac{x+3}{11}=\frac{y+4}{18}=\frac{z-0}{1}=\lambda
$
The general equation of plane and its normal is $a x+b y+c z+d=0$ and $\overrightarrow{\mathbf{n}}=a \hat{i}+b \hat{j}+c \hat{k}$

Then, $\overrightarrow{\mathbf{n}}_1=-3 \hat{i}+2 \hat{j}-3 \hat{k}$
and $\overrightarrow{\mathbf{n}}_2=2 \hat{i}-\hat{j}-4 \hat{k}$
$
\overrightarrow{\mathbf{s}}=\overrightarrow{\mathbf{n}}_1 \times \overrightarrow{\mathbf{n}}_2=\left|\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
-3 & 2 & -3 \\
2 & -1 & -4
\end{array}\right|=-11 \vec{i}-18 \vec{j}-\vec{k}, \quad \vec{s}=a \vec{i}+b \vec{j}+c \vec{k}
$
To write the equation of the line of intersection, i.e., $\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$, we still need the coordinates of any of its points $\mathrm{P}\left(\mathrm{x}_0, \mathrm{y}_0, \mathrm{z}_0\right)$.
Let this point be the intersection of the intersection line and the $X Y$ coordinate plane.
Then, the coordinates of the point of intersection ( $x, y, 0$ ) must satisfy the equations of the given planes.
Therefore, by putting $z=0$ into $P_1$ and $P_2$ we get,

$
\begin{aligned}
& -3 x+2 y-3(0)-1=0 \\
& 2 x-y-4(0)+2=0 \\
& x=-3 \text { and } y=-4
\end{aligned}
$
So the line of intersection is $\frac{x+3}{-11}=\frac{y+4}{-18}=\frac{z}{-1}$ or $\frac{x+3}{11}=\frac{y+4}{18}=\frac{z}{1}$

What is the Angle Between a Line and a Plane?

The angle between a line and a plane is the complement of the angle between the line and normal to the plane.

Equation of Angle Between a Line and a Plane in Vector Form

If the equation of the line is $\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_0+\lambda \overrightarrow{\mathbf{b}}$ and the equation of the plane is $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}=d$.

Then the angle $\theta$ between the line and the normal to the plane is

$
\cos \theta=\left|\frac{\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{n}}}{|\overrightarrow{\mathbf{b}}| \cdot|\overrightarrow{\mathbf{n}}|}\right|
$

and so the angle $\varphi$ between the line and the plane is given by $90^{\circ}-\theta$,

$
\sin (90-\theta)=\cos \theta
$

i.e.

$
\sin \phi=\left|\frac{\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{n}}}{|\overrightarrow{\mathbf{b}}| \cdot|\overrightarrow{\mathbf{n}}|}\right| \quad \text { or } \quad \phi=\sin ^{-1}\left|\frac{\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{n}}}{|\overrightarrow{\mathbf{b}}| \cdot|\overrightarrow{\mathbf{n}}|}\right|
$

Equation of Angle Between a Line and a Plane in Cartesian Form

The angle between a line and a plane
If the line is $\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}$ and the plane is $a_1 x+b_1 y+c_1 z+d=0$ is given by

$
\sin \theta=\frac{a_1 a+b_1 b+c_1 c}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a^2+b^2+c^2}}
$
NOTE:
Line $\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_0+\lambda \overrightarrow{\mathbf{b}}$ and plane $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}=d$ are perpendicular if $\overrightarrow{\mathbf{b}}=\lambda \overrightarrow{\mathbf{n}}$ or $\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{n}}=0$ and parallel if $\overrightarrow{\mathbf{b}} \perp \overrightarrow{\mathbf{n}}$ or $\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{n}}=0$

The intersection of a line and a plane

Given the equation of the line is $\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$ and the equation of the plane is $a x+b y+c z+d=0$

Let $\quad \frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}=r$

$
\therefore \quad\left(x=r l+x_1, y=m r+y_1, z=n r+z_1\right)
$

be a point in the plane say $P$.
It must satisfy the equation of plane.

$
\begin{array}{lc}
\therefore & a\left(x_1+l r\right)+b\left(y_1+m r\right)+c\left(z_1+n r\right)+d=0 \\
\Rightarrow & \left(a x_1+b y_1+c z_1+d\right)+r(a l+b m+c n)=0 \\
\Rightarrow & \quad r=-\frac{\left(a x_1+b y_1+c z_1+d\right)}{a l+b m+c n}
\end{array}
$
Put the value of r in $\left(x=r l+x_1, y=m r+y_1, z=n r+z_1\right)$, you will get the coordinates of point $P$.

Condition for a Line to be Parallel to a Plane

The line $\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$ is parallel to plane $\mathrm{ax}+\mathrm{by}+\mathrm{cz}$ $+d=0$ iff:
$\theta=0$ or $\pi$ or $\sin \theta=0 \Rightarrow a l+b m+c m=0$

Condition for a Line to Lie in the Plane

Condition for the line $\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$ to lie in the plane ax + by + cz + d = 0 are:

$
a l+b m+c n=0 \text { and } a x_1+b y_1+c z_1+d=0
$

Recommended Video Based on the Line of Intersection of Two Plane and the Angle Between a Line and a Plane

Solved Examples Based on the Line of Intersection of Two Plane and the Angle Between a Line and a Plane

Example 1: For $\mathrm{a}, \mathrm{b} \in \mathrm{Z}$ and $|a-b|<10$ let the angle between the plane $P: a x+y-z=b$ and the line $1: x-1=a-y=z$ +1 be $\cos ^{-1}\left(\frac{1}{3}\right)$. If the distance of the point $(6,-6,4)$ from the plane P is $3 \sqrt{6}$, then $a^4+b^2$ is equal to
[JEE MAINS 2023]

Solution
$
\begin{aligned}
& \theta=\cos ^{-1} \frac{1}{3} \therefore \sin \theta=\sqrt{1-\frac{1}{9}}=\frac{2 \sqrt{2}}{3} \\
& \sin \theta=\frac{a \cdot 1+1(-1)+(-1) \cdot 1}{\sqrt{a^2+1+1} \cdot \sqrt{3}}=\frac{2 \sqrt{2}}{3} \\
& \Rightarrow\{3(a-2)\}^2=24\left(a^2+2\right) \\
& \Rightarrow 3\left(a^2-4 a+4\right)=8 a^2+16 \\
& \Rightarrow 5 a^2+12 a+4=0 \\
& \Rightarrow 5 a^2+10 a+2 a+4=0 \\
& \therefore a=-2, \frac{-2}{5} \because a \in z \\
& \therefore a=-2
\end{aligned}
$
$\begin{aligned} & -2 x+y-z-b=0 \text { is } 3 \sqrt{6} \\ & \therefore\left|\frac{-12-6-4-b}{\sqrt{4+1+1}}\right|=3 \sqrt{6} \\ & \Rightarrow|b+22|=18 \therefore b=-40,-4 \\ & \because|a-b| \leq 10 \\ & \therefore \mathrm{b}=-4 \\ & \therefore a^4+b^2 \\ & =32 \end{aligned}$
Hence, the answer is 32

Example 2: Let the plane $x+3 y-2 z+6=0$ meet the coordinate axes at points $\mathrm{A}, \mathrm{B}$, and C. If the orthocenter of the triangle ABC is $\left(\alpha, \beta, \frac{6}{7}\right)$, then $98(\alpha+\beta)^2$ is equal to
[JEE MAINS 2023]
Solution

$
\begin{aligned}
& \mathrm{A}(-6,0,0) \mathrm{B}(0,-2,0) \mathrm{C}=(0,0,3) \\
& \overrightarrow{\mathrm{AB}}=6 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}, \overrightarrow{\mathrm{BC}}=2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}} \\
& \overrightarrow{\mathrm{AC}}=6 \hat{\mathrm{i}}+3 \hat{\mathrm{k}}
\end{aligned}
$

$\begin{aligned} & \overrightarrow{A H} \cdot \overrightarrow{B C}=0 \\ & \left(\alpha+6, \beta, \frac{6}{7}\right) \cdot(0,2,3)=0 \\ & \beta=\frac{-9}{7} \\ & \overrightarrow{\mathrm{CH}} \cdot \overrightarrow{\mathrm{AB}}=0 \\ & \left(\alpha, \beta, \frac{-15}{7}\right) \cdot(6,-2,0)=0 \\ & 6 \alpha-2 \beta=0 \\ & \alpha=\frac{-3}{7} \\ & 98(\alpha+\beta)^2=(98) \frac{(144)}{49}=288\end{aligned}$

Hence, the answer is 288

Example 3: Let N be the foot of the perpendicular from the point $\mathrm{P}(1,-2,3)$ on the line passing through the points $(4,5,8)$ and $(1,-7.5)$. Then the distance of N from the plane $2 x-2 y+z+5=0$ is
[JEE MAINS 2023]

Solution

$
\begin{aligned}
& \overrightarrow{\mathrm{PN}}=\langle\lambda, 4 \lambda-5, \lambda+2\rangle \\
& \overrightarrow{\mathrm{PN}} \cdot\langle 1,4,1\rangle=0 \\
& \Rightarrow \lambda+16 \lambda-20+\lambda+2=0 \\
& \Rightarrow \lambda=1 \\
& \mathrm{~N}(2,-3,6)
\end{aligned}
$
Distance of N from $2 x-2 y+z+5=0$ is

$
\begin{aligned}
\mathrm{d} & =\left|\frac{2(2)-2(-3)+6+5}{\sqrt{2^2+(-2)^2+(1)^2}}\right| \\
& =\left|\frac{21}{3}\right|=7
\end{aligned}
$

Hence, the answer is 7

Example 4: The plane $2 x-y+z=4$ intersects the line segment joining the points $A(a,-2,4)$ and $B(2, b,-3)$ at the point $C$ in the ratio $2: 1$ and the distance of the point $C$ from the origin is $\sqrt{5}$. If $a b<0$ and P is the point $(a-b, b, 2 b-a)$ then $C P^2$ is equal to
[JEE MAINS 2023]

Solution

$C$ divides $A B$ in $2: 1$

$
\begin{aligned}
& C\left(\frac{4+a}{3}, \frac{2 b-2}{3}, \frac{-6+4}{3}\right) \\
& C\left(\frac{a+4}{3}, \frac{2 b-2}{3}, \frac{-2}{3}\right)
\end{aligned}
$
C lies in the plane

$\begin{aligned} & \quad \therefore 2\left(\frac{a+4}{3}\right)-\left(\frac{2 b-2}{3}\right)+\left(\frac{-2}{3}\right)=4 \\ & \quad \Rightarrow 2 a-2 b=4 \\ & a-b=2 \\ & \because \mathrm{OC}=\sqrt{5} \\ & \quad \mathrm{OC}^2=5 \\ & \mathrm{C}\left(\frac{\mathrm{b}+6}{3}, \frac{2 b-2}{3}, \frac{-2}{3}\right)\end{aligned}$

$\Rightarrow\left(\frac{\mathrm{b}+6}{3}\right)^2+\left(\frac{2 \mathrm{~b}-2}{3}\right)^2+\left(\frac{-2}{3}\right)^2=5 \quad$ Now $\begin{array}{lr}\Rightarrow 5 b^2+4 b-1=0 & C\left(\frac{5}{3}, \frac{-4}{3}, \frac{-2}{3}\right) \\ \Rightarrow 5 b^2+5 b-b-1=0 & P(a-b, b, 2 b-a)\end{array}$

$\Rightarrow 5 \mathrm{~b}(\mathrm{~b}+1)-1(\mathrm{~b}+1)=0 \quad(2,-1,-3)$

$\mathrm{b}=-1 \& \frac{1}{5} \quad \mathrm{CP}^2=\left(\frac{5}{3}-2\right)^2+\left(\frac{-4}{3}+1\right)^2+\left(\frac{-2}{3}+3\right)^2=\frac{17}{3}$
$
\begin{aligned}
& \quad a=1 \\
& \because a b<0 \\
& \therefore a=1, b=-1
\end{aligned}
$
Hence, the answer is $\frac{17}{3}$

Example 5: Let the line $L: \frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-3}{1}$ intersect the plane $2 x+y+3 z=16$ at the point P . Let the point Q be the foot perpendicular to the point $R(1,-1,-3)$ on the line L . If \alpha is the area of triangle PQR , then $\alpha^2$ is equal to
$[$ JEE MAINS 2023]

Solution: The point on line L is $(2 \lambda+1,-\lambda-1, \lambda+3)$
If the above point is the intersection point of line $L$ and the plane then

$
\begin{aligned}
& 2(2 \lambda+1)+,(-\lambda-1), 3(\lambda+3)=16 \\
& \lambda=1 \\
& \text { Point } \mathrm{P}=(3,-2,4)
\end{aligned}
$

$\begin{aligned} & \text { Dr of } \mathrm{QR}=\langle 2 \lambda,-\lambda, \lambda+6\rangle \\ & \text { Dr of } \mathrm{L}=\langle 2-1,1\rangle \\ & \quad 4 \lambda+\lambda+\lambda+6=0 \\ & \lambda=-1 \\ & \mathrm{Q}=(-1,0,2)\end{aligned}$

$\begin{aligned} & \overrightarrow{\mathrm{QR}}=2 \hat{\mathrm{i}}-\hat{\mathrm{j}}-5 \hat{\mathrm{k}} \\ & \overrightarrow{\mathrm{QP}}=4 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}+2 \hat{\mathrm{k}} \\ & \overrightarrow{\mathrm{QR}} \times \overrightarrow{\mathrm{QP}}=\left|\begin{array}{ccc}\hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\ 2 & -1 & -5 \\ 4 & -2 & 2\end{array}\right|=-12 \hat{\mathrm{i}}-24 \hat{\mathrm{j}} \\ & \alpha=\frac{1}{2} \times \sqrt{144+576} \\ & \alpha^2=\frac{720}{4}=180 \\ & \alpha^2=180\end{aligned}$

Hence, the answer is 180

Summary

Intersecting planes are planes that are not parallel, and they always intersect in a line. Let the equation of two non-parallel planes be $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_1=d_1$ and $\overrightarrow{\mathbf{r}} \cdot \overrightarrow{\mathbf{n}}_2=d_2$. If the line of intersection of planes is perpendicular to $\overrightarrow{\mathbf{n}}_1$ and $\overrightarrow{\mathbf{n}}_2$, then, the line of intersection is parallel to vector $\overrightarrow{\mathbf{n}}_1 \times \overrightarrow{\mathbf{n}}_2$.