Location of Roots: Quadratic Equation, Theorem, Formula, Questions

Edited By Komal Miglani | Updated on Feb 08, 2025 09:09 PM IST

Quadratic equations are an important concept in algebra and have numerous applications in various fields including physics, engineering, and economics. Understanding the location of the roots of these equations is crucial, as it provides insight into the nature and behavior of the solutions.

In this article, we will cover the concept of location of roots of quadratic equations. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics

This Story also Contains

Different Cases of Roots of a Quadratic Equation
The Sum and Product of Roots
Location of Roots
Solved Examples Based on Location of Roots

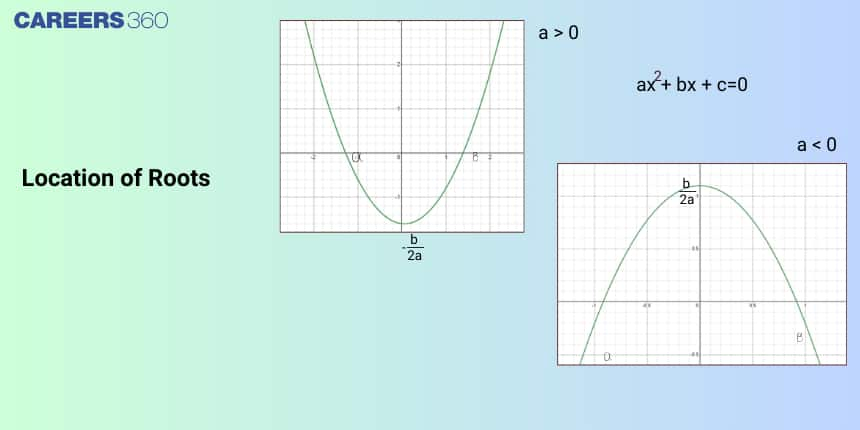
Location of Roots: Quadratic Equation, Theorem, Formula, Questions

Different Cases of Roots of a Quadratic Equation

1) When $D>0$ : Real and distinct

2) When $D=0$ : Real and equal

3) When $D<0$ : Imaginary and in pairs

4) When $D$ is a perfect square, then the roots are rational.

5) When $D$ is not a perfect square, then the roots are irrational.

The Sum and Product of Roots

Assume α and β to be the roots of a quadratic equation.

Sum of roots

$\begin{gathered}\alpha+\beta=\frac{-b+\sqrt{D}}{2 a}+\frac{-b-\sqrt{D}}{2 a} \\ =\left(\frac{-b}{2 a}+\frac{\sqrt{D}}{2 a}\right)+\left(\frac{-b}{2 a}-\frac{\sqrt{D}}{2 a}\right) \\ =\frac{-b}{2 a}+\frac{\sqrt{D}}{2 a}-\frac{b}{2 a}-\frac{\sqrt{D}}{2 a} \\ =\frac{-2 b}{2 a} \\ =\frac{-b}{a}\end{gathered}$

Product of roots

$
\begin{gathered}
\alpha \cdot \beta=\left(\frac{-b+\sqrt{D}}{2 a}\right) \cdot\left(\frac{-b-\sqrt{D}}{2 a}\right) \\
=\frac{(-b)^2-(\sqrt{D})^2}{(2 a)^2} \\
=\frac{b^2-D}{4 a^2} \\
=\frac{b^2-\left(b^2-4 a c\right)}{4 a^2} \quad\left[D=b^2-4 a c\right] \\
=\frac{4 a c}{4 a^2} \\
=\frac{c}{a}
\end{gathered}
$

A quadratic equation can be formed using the sum and product of the roots:

$
\begin{gathered}
x^2-(\alpha+\beta) x+(\alpha \cdot \beta)=0 \\
x^2-\frac{b}{a} x+\frac{c}{a}=0 \\
a x^2-b x+c=0
\end{gathered}
$

Location of Roots

A polynomial equation in which the highest degree of a variable term is 2 is called a quadratic equation.

Standard form of quadratic equation is $a x^2+b x+c=0$
Where $a$, $b$, and $c$ are constants (they may be real or imaginary) and called the coefficients of the equation and $a$ is also called the leading coefficient.

$
\text { Eg, }-5 x^2-3 x+2=0, x^2=0,(1+i) x^2-3 x+2 i=0
$
As the degree of the quadratic polynomial is 2 , so it always has 2 roots (number of real roots + number of imaginary roots $=2$ )

Let $\mathrm{f}(\mathrm{x})=\mathrm{ax}{ }^2+\mathrm{bx}+\mathrm{c}$, where $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are real numbers and ' a ' is non-zero number. Let $x_1$ and $x_2$ be the roots of the equation, and let k be a real number. Then:

1. If both roots of $\mathrm{f}(\mathrm{x})$ are less than k then

j) $\mathrm{D} \geq 0$ (as the real roots may be distinct or equal)
ii) $af( k)>0$ (In both the cases $af(\mathrm{k})$ is positive, as in second case if a $<0$ then $\mathrm{f}(\mathrm{k})<0$, so multiplying two $-ve$ values will give us a positive value)
iii) $k>\frac{-b}{2 a}$ since $\frac{-b}{a}$ will lie between $x_1$ and $x_2$, and $x_1$, $x_2$ are less than k so $\frac{-\mathrm{b}}{2 \mathrm{a}}$ will be less than k .

2. If both roots of $f(x)$ are greater than $k$

i) $\mathrm{D} \geq 0$ (as the real roots may be distinct or equal)
ii) $\mathrm{af}(\mathrm{k})>0$ (In both the cases af( k$)$ is positive, as in second case if a $<0$ then $\mathrm{f}(\mathrm{k})<0$, so multiplying two -ve values will give us a positive value)
iii) $k<\frac{-\mathrm{b}}{2 \mathrm{a}}$ since $\frac{-\mathrm{b}}{2 \mathrm{a}}$ will lie between $x_1$ and $x_2$, and $x_1$, $x_2$ are greater than k so $\frac{-\mathrm{b}}{2 \mathrm{a}}$ will be greater than k .

Condition for number $k$

Let $\mathrm{f}(\mathrm{x})=\mathrm{ax}^2+\mathrm{bx}+\mathrm{c}$ where $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are real numbers and ' a ' is non-zero number. Let $x_1$ and $x_2$ be the real roots of the function. And let k is any real number. Then:
1. If lies between the root $x_1$ and $x_2$

$\mathrm{af}(\mathrm{k})<0$.

As if $a<0$ then $f(k)>0$. So multiplying one $-ve$ and one $+ve$ value will give us negative value)

Condition for number $k_1$ and $k_2$

Let $f(x)=a x^2+b x+c$ where a,b,c are real numbers and ‘a’ is non-zero number. Let $x_1$ and $x_2$ be the real roots of the function. And let $k_1, k_2$ be any two real numbers. Then:

2. If exactly one root of $f(x)$lies in between the number $k_1, k_2$

$f\left(k_1\right) f\left(k_2\right)<0$ as for one value of k, we will have +ve value of$f(x)$ and for other vlaue of $k$, we will have $-ve$ value of $f(x)$ (here $x_1$ < $x_2$)

Condition on number $k_1, k_2$

Let $\mathrm{f}(\mathrm{x})=\mathrm{ax}{ }^2+\mathrm{bx}+\mathrm{c}$, where $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are real numbers and '$a$ ' is non-zero number. Let $x_1$ and $x_2$ be the roots of the function. And let $k 1, k_2$ be any two real numbers. Then

1. If both roots lie between $k_1, k_2$

i) $\mathrm{D} \geq 0$ (as the real roots may be distinct or equal)
ii) $k_1<\frac{-b}{2 a}<k_2$, where $a \leq 3$ and $k_1<k_2$
2. If $k_1, k_2$ lies between the roots

$\mathrm{af}\left(\mathrm{k}_1\right)<0$ and $\mathrm{af}\left(\mathrm{k}_2\right)<0$

Solved Examples Based on Location of Roots

Example 1: What is the value of m so that both roots of the equation $x^2+m x+1$ are less than unity?

1) $-2 ≥ m$

2) $2 ≥ m$

3) $m ≥ -2$

4) $m ≥ 2$

Solution

Location of roots (1) -

let $f(x)=a x^2+b x+c$ where $a, b, c$ is from real number and ' $a$ ' is non-zero number. Let $x_1$ and $x_2$ be the solution of the function. And let $k$ is number from real number. Then:
If both roots of $f(x)$ are less than $k$ then
$\mathrm{j} \geq 0$ (as roots may be equal)
Fi) af( $(\mathrm{k})>0$. As if a $<0$ then $\mathrm{f}(\mathrm{k})<0$. So multiplying two -ve value will give us a positive value, so af $(\mathrm{k})>0$ satisfies
III) $k>\frac{-b}{2 a}$ since, $\frac{-b}{2 a}$ will lies between $x_1$ and $x_2$, and $x_1$, $x_2$ are less than $k$ so $\frac{-b}{2 a}$ will be less than $k$.
since roots are less than unity it implies that $\mathrm{af}(1)>0$, here $a=1 \mathrm{f}(1)=\mathrm{m}+2$
So $m+2>0 \Rightarrow m>-2($ i $)$
2nd for two root to exist $\mathrm{D}>0 \Rightarrow \mathrm{m}^2-4 \geq 0$
So $m \geq 2$ or $m \leq-2$ (ii)
Combining (i) and (i) equation, we get
$\mathrm{m} \geq 2$

Correct option is (d)

Example 2: Find the value of a for which the equation $x^2-3 a x+2 a^2+a-3=0$ has real roots and both the roots are less than $1$
$
\text { 1) } a \in\left(-\infty, \frac{2-\sqrt{30}}{6}\right) \cup\left(\frac{2+\sqrt{4+24}}{6}, \infty\right)
$

2) $a \in(-\infty, 1) \cup(3, \infty)$
3) $u \in\left(-\infty,-\frac{2}{3}\right) \cup\left(1, \frac{2}{3}\right)$
4) $a \in\left(-\infty, \frac{2}{3}\right) \cup(3, \infty)$

(i) $ D>0$

$x^2-3 a x+2 a^2+a-3>0$

$B^2-4 A C>0$

$\begin{aligned} & 9 a^2-4\left(2 a^2+a-3\right)(1)>0 \\ & a^2-4 a+12>0 \\ & (a-2)^2+8>0 \\ & a \in R\end{aligned}$

(ii) $-\frac{B}{2 A}<1$

$
\begin{aligned}
& -\frac{-3 a}{2}<1 \\
& a<\frac{2}{3}
\end{aligned}
$

(iii) $a f(1)>0$

$\begin{aligned} & 1^2-2 a(1)+3 a^2+a-3>0 \\ & 3 a^2-a-2>0\end{aligned}$

$a \in\left(-\infty, \frac{1-\sqrt{ } 1+24}{6}\right) \cup\left(\frac{1+\sqrt{ } 1+24}{6}, \infty\right)$

$
a \in\left(-\infty,-\frac{2}{3}\right) \cup(1, \infty
$

From (i), (ii), and (iii)

$
a \in\left(-\infty,-\frac{2}{3}\right) \cup\left(1, \frac{2}{3}\right.)
$

Example 3: Find the value of $k$ for which both roots of the equation $x^2-4 k x-4-k+9 k^2=0$ are positive

1) $k \in\left(-\frac{4}{5}, 1\right)$

2) $k \in \phi$

3) $k>\frac{5}{2}$

4) $k \in\left(-\infty, \frac{7-\sqrt{135}}{6}\right) \cup\left(\frac{7+\sqrt{135}}{6}, \infty\right)$

Solution

i) $D \geq 0$

$\begin{aligned} & (-4 k)^2-4\left(-4-k+9 k^2\right) \geq 0 \\ & 16 k^2+16+4 k-36 k^2 \geq 0 \\ & 5 k^2-k-4 \leq 0 \\ & k \in\left[-\frac{4}{5}, 1\right]\end{aligned}$

ii) $a.f(0)>0$

$
0-4 k(0)-4-k+9 k^2>0
$

From (i), (ii) and (iii)

$k \in \varnothing$ or for no values of k sum of the roots is greater than 5

Example 4: The set of all real values of $\lambda$ for which the quadratic equations,

$\left(\lambda^2+1\right) x^2-4 \lambda x+2=0$ always have exactly one root in the interval $(0, 1)$ is :

1) $0,2$
2) $(2,4$
3) $(1,3)$
4) $-3,-1)$

Solution

If exactly one root in $(0, 1)$ then

$\begin{aligned} & \Rightarrow \mathrm{f}(0) \cdot \mathrm{f}(1)<0 \\ & \Rightarrow 2\left(\lambda^2-4 \lambda+3\right)<0 \\ & \Rightarrow 1<\lambda<3\end{aligned}$

Now for $\lambda=1$

$\begin{aligned} & 2 x^2-4 x+2=0 \\ & (x-1)^2=0 \\ & x=1.1\end{aligned}$

So both roots doesn’t lie between (0, 1)

$\therefore \lambda \neq 1$

$\begin{aligned} & \text { Again for } \lambda=3 \\ & 10 x^2-12 x+2=0 \\ & \Rightarrow x=1, \frac{1}{5}\end{aligned}$

So if one root is $1$ then second root lie between $(0, 1)$ so $\lambda=3$

$\therefore \lambda \in(1,3)$

Example 5: If both the roots of the quadratic equation $x^2-2 p x+p^2+p-5=0$ are less than $3$, then the largest integral value of $p$ is________.

1)$ 0$

2) $1$

3) $2$

4) $3$