Permutation: Definition, Formula, Types, and Examples

Permutation basically means the arrangement of things. And when we talk about arrangement then the order becomes important if the things to be arranged are different from each other (when things to be arranged are the same then order doesn’t have any role to play). So in permutations order of objects becomes important. In real life, we use permutation for arranging numbers, letters, codes, and alphabets.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Permutation: Definition
2. Permutation Formula
3. Arranging n objects in r places (Same as arranging n objects taken r at a time) is equivalent to filling r places from n things.
4. Permutation of n different objects
5. Solved Examples Based on Permutation
6. Example 1: Eight persons are to be transported from city A to city B in three cars of different makes. If each car can accommodate at most three persons, then the number of ways, in which they can be transported, is[JEE MAINS 2023]
7. The permutations represent the number of distinct arrangements of objects where the order matters. The calculation of permutations using factorial notation provides a precise method to quantify and analyze sequential arrangements. Understanding of permutation is necessary for solving complex problems.

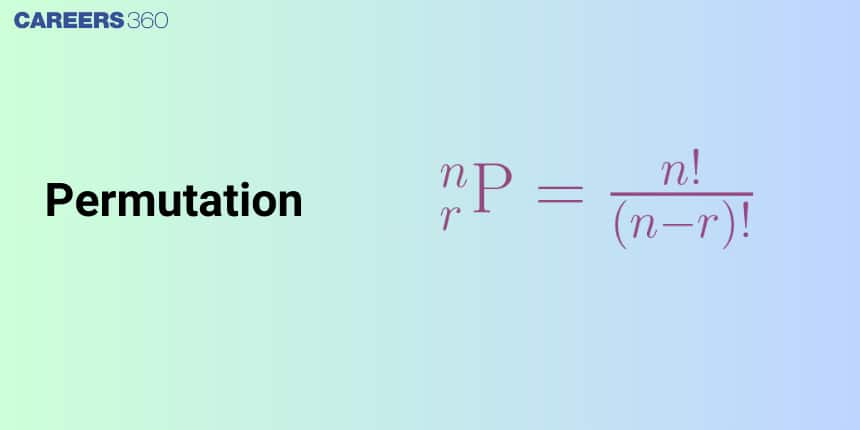
In this article, we will cover the Introduction Of Permutation. This topic falls under the broader category of Permutations and combinations, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of thirteen questions have been asked on this topic in JEE Main from 2013 to 2023 including one in 2013, one in 2014, two in 2020, one in 2021, and eight in 2023.

Permutation: Definition

A permutation is an arrangement of all or part of a set of objects, with regard to the order of the arrangement.

Arranging n objects in r places (Same as arranging n objects taken r at a time) is equivalent to filling $r$ places from $n$ things.

For example, suppose we have a set of three letters: A, B, and C. We want to find the number of ways in which 2 letters from this set can be arranged. Each possible arrangement would be an example of a permutation. The complete list of possible permutations would be $AB,AC$, $BA,BC,CA$, and $CB$. Thus there 6 number of permutations. We observe that the order in which letters are occurring is important, i.e., AB and BA are two different arrangements. In mathematics, we use a specific terminology. That is "permutations as $n$ distinct objects taken $r$ at a time". Here n refers to the number of objects from which the permutation is formed, and $r$ refers to the number of objects used to form the permutation. In the above example, the permutation was formed from 3 letters (A, B, and C), so $n=3$ and the permutation consisted of 2 letters, so $\mathrm{r}=$.

Permutation Formula

Arranging $n$ objects in $r$ places (Same as arranging $n$ objects taken $r$ at a time) is equivalent to filling $r$ places from $n$ things.

r places:
$$\text{Unknown environment 'tabular'}$$
$◻$ number of choices: $n$ ( $n-1)(n-2)(n-3)$
$n-(r-1)$

So the number of ways of arranging $n$ objects taken $r$ at a time $=n(n-1)$ $(n-2)\dots (n-r+1)$

$\frac{n(n-1)(n-2)\dots (n-r+1)(n-r)!}{(n-r)!}=\frac{n!}{(n-r)!}={}^n{P}_r$

Where $r\le n$ and $r\in W$

So, the number of ways arranging n different objects taken all at a time $=$ ${}^{ı}{P}_n=n!$

Example: In how many ways can 5 people be seated at 3 places?

Solution: Basically this question is about arranging 5 people at 3 different places

Let's think that we are given 3 places, so for the first place we have 5 people to choose from, hence this can be done in 5 ways as all 5 are available.

Now for 2nd place we have 4 people to choose from, hence this can be done in 4 ways.

Similarly, for 3rd place, we have 3 choices.
Since we have to choose for all 3 places, so multiplication rule is applicable, and the total number of ways $5\times 4\times 3=120$,

This can also be done directly from the notation or formula

${}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{r}}\text{where}\mathrm{n}=5,\mathrm{r}=3,\text{so}{}^5{\mathrm{P}}_3=\frac{5!}{2!}=5\times 4\times 3=120$
Example: Find the number of ways the letters of the word "BIRTHDAY" can be arranged taken all at a time.

Solution: From the above concept directly using the formula ${}^n{\mathrm{P}}_{\mathrm{n}}$ we have

${}^8{\mathrm{P}}_8=8!=40,320$

Types of Permutation

Permutation can be classified into three different categories:

• Permutation of n different objects (when repetition is not allowed)

• Repetition, where repetition is allowed

• Permutation when the objects are not distinct (Permutation of multisets)

Permutation of n different objects

If $n$ is a positive integer and $r$ is a whole number, such that $r<n$, then $P(n$, r) represents the number of all possible arrangements or permutations of n distinct objects taken r at a time. In the case of permutation without repetition, the number of available choices will be reduced each time. It can also be represented as ${}^n{P}_r$.

$P(n,r)=n!/(n-r)!$

Permutation when repetition is allowed

When the number of objects is " $n$," and we have " $r$ " to be the selection of object, then;

Choosing an object can be in $n$ different ways.
Thus, the permutation of objects when repetition is allowed will be equal to,

$n\times n\times n\times \dots \dots (r\text{times})=n^r$
Permutation of multi-sets

Permutation of n different objects when ${\mathrm{P}}_1$ objects among ' $n$ ' objects are similar, ${\mathrm{P}}_2$ objects of the second kind are similar, ${\mathrm{P}}_3$ objects of the third kind are similar $$ and so on, ${\mathrm{P}}_{\mathrm{k}}$ objects of the kth kind are similar and the remaining of all is of a different kind,

Thus it forms a multiset, where the permutation is given as:

$\frac{n!}{P_1!P_2!\dots P_n!}$

Relation Between Combination And Permutations

The relation between combinations and permutations is given by

${}^n{C}_r\times r!={}^n{P}_r$
Factorial notation

Many times we multiplied consecutive integers. On the basis of this factorial notation is devised. In the counting principle many times answer is written in the form of factorial to save us time. The product of first $n$ natural numbers is denoted by $\mathrm{n}!$ and is read as 'factorial n '.

Note:
The factorial of zero is defined and its value is one.

Solved Examples Based on Permutation

Example 1: Eight persons are to be transported from city A to city B in three cars of different makes. If each car can accommodate at most three persons, then the number of ways, in which they can be transported, is
[JEE MAINS 2023]

Solution

<svg xmlns="http://www.w3.org/2000/svg" width="600" height="473" viewBox="0 0 600 473">
<metadata>
<molecule>
<smiles>**(*)*</smiles>
<mol>
Mathpix
2D

4 3 0 0 0 0 0 0 0 0999 V2000
6.2033 -1.3790 0.0000 R 0 0 0 0 0 0 0 0 0 0 0 0
2.0327 -5.6822 0.0000 R 0 0 0 0 0 0 0 0 0 0 0 0
7.5350 -5.2274 0.0000 R 0 0 0 0 0 0 0 0 0 0 0 0
6.3785 -9.2507 0.0000 R 0 0 0 0 0 0 0 0 0 0 0 0
1 2 1 0
2 3 1 0
2 4 1 0
A 1
3
A 2
8
A 3
3
A 4
2
M END
</mol>
<inchi></inchi>
<inchi_key></inchi_key>
</molecule>
</metadata>
<rect style='opacity:1.0;fill:#FFFFFF;stroke:none' width='600.0' height='473.0' x='0.0' y='0.0'> </rect>
<path class='bond-0 atom-0 atom-1' d='M 355.9,52.1 L 176.7,237.1' style='fill:none;fill-rule:evenodd;stroke:#191919;stroke-width:2.0px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1' />
<path class='bond-1 atom-1 atom-2' d='M 176.7,253.5 L 424.1,233.1' style='fill:none;fill-rule:evenodd;stroke:#191919;stroke-width:2.0px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1' />
<path class='bond-2 atom-1 atom-3' d='M 176.7,269.2 L 364.8,423.7' style='fill:none;fill-rule:evenodd;stroke:#191919;stroke-width:2.0px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1' />
<path class='atom-0' d='M 376.0 34.2
Q 378.1 34.8, 379.1 36.2
Q 380.2 37.5, 380.2 39.7
Q 380.2 41.5, 379.2 43.0
Q 378.3 44.4, 376.6 45.2
Q 374.9 46.0, 372.7 46.0
Q 370.4 46.0, 368.6 45.2
Q 366.9 44.3, 365.5 42.7
L 367.3 40.9
Q 368.6 42.4, 369.8 42.9
Q 370.9 43.5, 372.7 43.5
Q 374.7 43.5, 375.9 42.4
Q 377.1 41.4, 377.1 39.7
Q 377.1 37.4, 375.8 36.5
Q 374.6 35.4, 371.9 35.4
L 370.4 35.4
L 370.4 33.2
L 371.7 33.2
Q 374.1 33.2, 375.4 32.2
Q 376.6 31.1, 376.6 29.2
Q 376.6 27.8, 375.6 27.0
Q 374.5 26.1, 372.8 26.1
Q 370.9 26.1, 369.8 26.8
Q 368.7 27.4, 367.8 29.0
L 365.7 27.9
Q 366.5 26.1, 368.3 24.9
Q 370.2 23.6, 372.8 23.6
Q 376.0 23.6, 377.8 25.2
Q 379.7 26.7, 379.7 29.2
Q 379.7 31.0, 378.8 32.2
Q 377.8 33.5, 376.0 34.2
' fill='#191919'/>
<path class='atom-1' d='M 162.7 254.4
Q 164.7 255.3, 165.9 256.6
Q 167.0 257.8, 167.0 260.0
Q 167.0 261.8, 166.1 263.3
Q 165.1 264.7, 163.4 265.5
Q 161.7 266.3, 159.5 266.3
Q 155.8 266.3, 153.7 264.6
Q 151.7 262.9, 151.7 260.0
Q 151.7 258.2, 152.6 256.9
Q 153.5 255.5, 155.4 254.5
Q 154.0 253.7, 153.2 252.6
Q 152.5 251.4, 152.5 249.5
Q 152.5 247.0, 154.3 245.5
Q 156.2 244.0, 159.3 244.0
Q 162.5 244.0, 164.3 245.5
Q 166.2 247.0, 166.2 249.5
Q 166.2 251.1, 165.3 252.3
Q 164.5 253.5, 162.7 254.4
M 159.3 246.3
Q 157.5 246.3, 156.5 247.1
Q 155.5 248.0, 155.5 249.5
Q 155.5 250.7, 156.2 251.4
Q 156.9 252.2, 157.8 252.6
Q 158.8 253.0, 160.7 253.7
Q 162.0 252.7, 162.6 251.8
Q 163.1 250.8, 163.1 249.5
Q 163.1 248.0, 162.1 247.1
Q 161.1 246.3, 159.3 246.3
M 159.5 264.0
Q 161.5 264.0, 162.7 262.9
Q 163.9 261.8, 163.9 260.0
Q 163.9 258.8, 163.3 258.1
Q 162.7 257.3, 161.7 256.9
Q 160.7 256.5, 159.0 255.9
L 157.6 255.4
Q 156.1 256.4, 155.4 257.5
Q 154.7 258.6, 154.7 260.0
Q 154.7 261.8, 156.0 262.9
Q 157.3 264.0, 159.5 264.0
' fill='#191919'/>
<path class='atom-2' d='M 444.2 231.2
Q 446.3 231.8, 447.3 233.2
Q 448.3 234.6, 448.3 236.7
Q 448.3 238.6, 447.4 240.0
Q 446.5 241.4, 444.8 242.2
Q 443.1 243.0, 440.9 243.0
Q 438.6 243.0, 436.8 242.2
Q 435.1 241.3, 433.7 239.7
L 435.5 237.9
Q 436.8 239.4, 438.0 240.0
Q 439.1 240.5, 440.9 240.5
Q 442.9 240.5, 444.1 239.5
Q 445.3 238.4, 445.3 236.7
Q 445.3 234.5, 444.0 233.5
Q 442.8 232.5, 440.1 232.5
L 438.5 232.5
L 438.5 230.3
L 439.9 230.3
Q 442.3 230.2, 443.6 229.2
Q 444.8 228.2, 444.8 226.2
Q 444.8 224.8, 443.8 224.0
Q 442.7 223.1, 440.9 223.1
Q 439.1 223.1, 438.0 223.8
Q 436.9 224.4, 436.0 226.1
L 433.9 224.9
Q 434.7 223.1, 436.5 221.9
Q 438.4 220.7, 440.9 220.7
Q 444.1 220.7, 446.0 222.2
Q 447.9 223.7, 447.9 226.2
Q 447.9 228.0, 446.9 229.2
Q 446.0 230.5, 444.2 231.2
' fill='#191919'/>
<path class='atom-3' d='M 374.6 431.0
Q 375.4 429.0, 377.3 427.8
Q 379.2 426.7, 381.8 426.7
Q 385.1 426.7, 386.9 428.4
Q 388.8 430.2, 388.8 433.4
Q 388.8 436.6, 386.4 439.6
Q 384.0 442.6, 379.1 446.2
L 389.2 446.2
L 389.2 448.7
L 374.5 448.7
L 374.5 446.6
Q 378.6 443.7, 380.9 441.6
Q 383.4 439.4, 384.5 437.5
Q 385.7 435.5, 385.7 433.5
Q 385.7 431.4, 384.7 430.3
Q 383.6 429.1, 381.8 429.1
Q 380.1 429.1, 378.9 429.8
Q 377.7 430.5, 376.9 432.1
L 374.6 431.0
' fill='#191919'/>
</svg>

$\begin{array}{rl}& \text{Ways}=\frac{8!}{3!3!2!2!}\times 3!\\ & =\frac{8\times 7\times 6\times 5\times 4}{4}\\ & =56\times 30\\ & =1680\end{array}$

Hence, the answer is 1680

Example 2: The letters of the word OUGHT are written in all possible ways and these words are arranged as in a dictionary, in a series. Then the serial number of the word TOUGH is
[JEE MAINS 2023]

Solution

G H O TU
$$\text{Unknown environment 'tabular'}$$ & & \
\hline & TOU & & & \
\hline & TOUG \lfloor & & 1 & \
\hline & & & 89 & \
\hline
\end{tabular}

Hence, the answer is 89

Example 3: The number of seven digits odd numbers, that can be formed using all the seven digits $1,2,2,2,3,3,5$ is $$
[JEE MAINS 2023]
Solution The no. of 7-digit odd Numbers that can be formed using 1, 2, 2, $2,3,3,5$

$$\text{Unknown environment 'tabular'}$$
$\frac{\underset{―}{6}}{\underset{―}{3}\lfloor 2}=\frac{720}{12}=60$ $=240$

Hence, the answer is 240
Example 4: The number of 4-letter words, with or without meaning, each consisting of 2 vowels and 2 consonants, which can be formed from the letters of the word UNIVERSE without repetition is
[JEE MAINS 2023]
Solution: UNIVERSE:
$$\text{Unknown environment 'tabular'}$$

= 240

Hence, the answer is 240

Example 4: The number of 4-letter words, with or without meaning, each consisting of 2 vowels and 2 consonants, which can be formed from the letters of the word UNIVERSE without repetition is [JEE MAINS 2023]

Solution: UNIVERSE:

2 vowels different, 2 consonants different

$\begin{array}{rl}& \left({}^3{\mathrm{C}}_2\right)\left({}^4{\mathrm{C}}_2\right)(4!)\\ & =(3)(6)(24)\\ & =432\end{array}$

Hence, the answer is 432.

Example 5: The number of integers, greater than 7000 that can be formed, using the digit $3,5,6,7,8$ without repetition, is
[JEE MAINS 2023]
Solution
C-1

$\begin{array}{rl}& 2\times 4\times 3\times 2=48\\ & C-25!(5\text{digit nos})=\frac{120}{168}\end{array}$

Hence, the answer is 168

Summary

The permutations represent the number of distinct arrangements of objects where the order matters. The calculation of permutations using factorial notation provides a precise method to quantify and analyze sequential arrangements. Understanding of permutation is necessary for solving complex problems.

Recommended Video :

Frequently Asked Questions (FAQs)
Q1) What is permutations?
Answer: A permutation is an arrangement of all or part of a set of objects, with regard to the order of the arrangement.
Q2) What is the number of ways of arranging $n$ objects taken $r$ at a time?
Answer: The number of ways of arranging $n$ objects taken $r$ at a

$\text{time}={}^n{P}_r$
Where $r\le n$ and $r\in W$
Q3) What is the number of ways arranging n different objects taken all at a time?
Answer: the number of ways arranging n different objects taken all at a time $={}^n{P}_n=n!$
Q4) What is the factorial of zero?
Answer: The factorial of zero is defined and its value is one.
Q5) What is factorial notation?
Answer: Many times we multiplied consecutive integers. On the basis of this factorial notation is devised. The product of first $n$ natural numbers is denoted by $n!$ and is read as 'factorial $n$ '.