Polar Form of Complex Number - Meaning, Formula and Examples

The polar form is an alternative representation of complex numbers. A number of the form a + ib is called a complex number (where a and b are real numbers and i is iota). We usually denote a complex number by the letter $z,z_1,z_2$ etc. Typically, a complex number is expressed in rectangular form as $z=ai+b$, where (a,b) are the rectangular coordinates. In polar form, the complex number is described using its modulus and argument. It is generally represented by $x+iy=r\cos \theta +ir\sin \theta$ where r is the modulus of the complex number and $\theta$ is the argument of the complex number.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. What are Complex Numbers?
2. What is the Polar Form of Complex Numbers?
3. Equation of Polar Form of Complex Numbers
4. Conversion from Rectangular Form to Polar Form of Complex Number
5. Adding Complex numbers in Polar Form
6. Product of Polar Form of Complex Number
7. Important points

In this article, we will cover the concept of the polar form of a complex number. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of six questions have been asked on this concept, including one in 2013, one in 2015, one in 2018, two in 2019, and one in 2022.

What are Complex Numbers?

The number which has no real meaning then these numbers are represented in complex forms. The general form of complex numbers are $a+ib$ where i is iota or$\sqrt{-1}$.

A number of the form$a+ib$ is called a complex number (where a and b are real numbers and i is iota). We usually denote a complex number by the letter $z_1,z_1,z_2$ etc

For example,$z=5+2i$ is a complex number.

5 here is called the real part and is denoted by Re(z), and 2 is called the imaginary part and is denoted by Im(z)

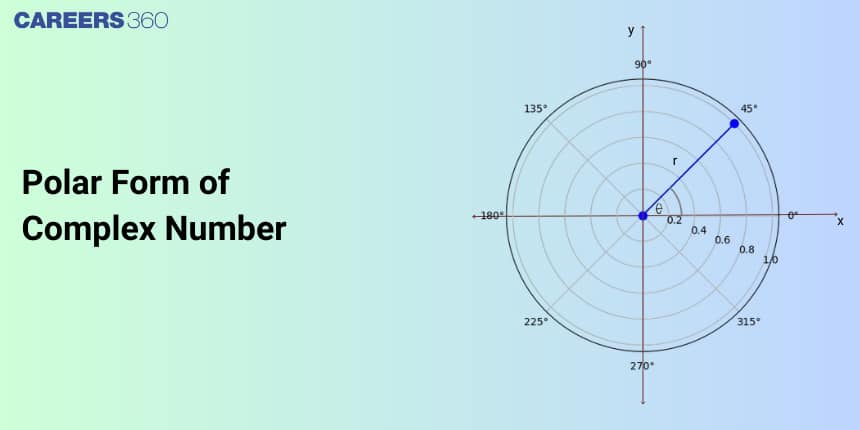
What is the Polar Form of Complex Numbers?

In polar form, we represent the complex number through the argument and modulus value of complex numbers.

Let $z=x+iy$ be a complex number,

And we know that

$|z|=\sqrt{x^2+y^2}=r$

And let arg(z) = θ

• The horizontal and vertical axes are the real axis and the imaginary axis, respectively.
• $r$ - the length of the vector and $\theta$ - the angle made with the real axis, are the real and complex components of the polar form of the complex number.
• There is a point P with coordinates $(x,y)$.
• The distance from the origin $(0,0)$ to point $P$ is given as $r$.
• The line joining the origin to point P makes an angle $\theta$ with the positive $x$ -axis.
• The polar coordinates are given as $(r,\theta )$ and rectangular coordinates are given as $(x,y)$.

Equation of Polar Form of Complex Numbers

From the figure, $x=|z|\cos (\theta )=r\cos (\theta )$
and $y=|z|\sin (\theta )=r\sin (\theta )$
So, $z=x+iy=r\cos (\theta )+i\cdot r\sin (\theta )=r(\cos (\theta )+i\cdot \sin (\theta ))$
This form is called polar form with $\theta =$ principal value of $\arg (z)$ and $r=|z|$.
For general values of the argument
$\mathrm{z}=\mathrm{r}[\cos (2\mathrm{n}\pi +\theta )+i\sin (2\mathrm{n}\pi +\theta )]$, where $n\in$ Integer

Conversion from Rectangular Form to Polar Form of Complex Number

The conversion of complex number $z=a+bi$ from rectangular form to polar form is done using the formula $r=\sqrt{(a^2+b^2)},\theta ={\tan }^{-1}(b/a)$. Consider the complex number $z=-2+2\sqrt{3}i$. We note that $z$ lies in the second quadrant.

Using Pythagoras Theorem, the distance of $z$ from the origin, or the magnitude of $z$, is $|z|=\sqrt{(-2{)}^2+(2{\sqrt{3}}^2)})=\sqrt{(4+12)}=\sqrt{16}=4$. Now, let us calculate the angle between the line segment joining the origin to $z$ (OP) and the positive real direction (ray OX). Note that the angle POX' is ${\tan }^{-1}(2\sqrt{3}/(-2))={\tan }^{-1}(-\sqrt{3})=-{\tan }^{-1}(\sqrt{3})$. Since the complex number lies in the second quadrant, the argument $\theta =-{\tan }^{-1}(\sqrt{3})+{180}^{\circ }=-{60}^{\circ }$ $+{180}^{\circ }={120}^{\circ }$. So, the polar form of complex number $z=-2+2\sqrt{3}$ i will be $4(\cos {120}^{\circ }+i\sin {120}^{\circ })$

Adding Complex numbers in Polar Form

Let $3+5i$, and $7\mathrm{\angle }{50}^{\circ }$ are the two complex numbers.
First, we will convert $7\mathrm{\angle }{50}^{\circ }$ into a rectangular form.

$7\mathrm{\angle }{50}^{\circ }=x+iy$

Hence,

$\begin{array}{rl}& x=7\cos {50}^{\circ }=4.5\\ & y=7\sin {50}^{\circ }=5.36\end{array}$

So,

$7\mathrm{\angle }{50}^{\circ }=4.5+i5.36$

Therefore, if we add the two given complex numbers, we get;

$(3+i5)+(4.5+i5.36)=7.5+i10.36$

Modulus is equal to;

$\begin{array}{rl}& r=|z|=\sqrt{}(x^2+y^2)\\ & r=\sqrt{}({7.5}^2+{10.36}^2)\\ & r=12.79\end{array}$
And the argument is equal to;

$\begin{array}{rl}& \theta ={\tan }^{-1}(y/x)\\ & \theta ={\tan }^{-1}(10.36/7.5)\\ & \theta ={54.1}^{\circ }\end{array}$

Therefore, the required complex number is $12.79<{54.1}^{\circ }$.

Product of Polar Form of Complex Number

Let us consider two complex numbers in polar form, $z=r_1(\cos {\theta }_1+i\sin {\theta }_1),w=r_2(\cos {\theta }_2+i\sin {\theta }_2)$, Now, let us multiply the two complex numbers:

$\begin{array}{rl}& zw=r_1(\cos {\theta }_1+i\sin {\theta }_1)\times r_2(\cos {\theta }_2+i\sin {\theta }_2)\\ & =r_1{r}_2[(\cos {\theta }_1\cos {\theta }_2-\sin {\theta }_1\sin {\theta }_2)+i(\sin {\theta }_1\cos {\theta }_2+\cos {\theta }_1\sin {\theta }_2)]\\ & =r_1{r}_2[\cos ({\theta }_1+{\theta }_2)+i\sin ({\theta }_1+{\theta }_2)]\end{array}$

Important points

- The values of polar and rectangular coordinates depend on each other. If we know any two values, the remaining two values can be found easily using the relation established between them.
- The conversion formulas for rectangular to polar coordinates are given as $r=\sqrt{}(x^2+y^2)$ and $\theta ={\tan }^{-1}(\mathrm{y}/\mathrm{x})$.
- It is easy to see that for an arbitrary complex number $z=x+yi$, its modulus will be $|z|=$ $\sqrt{}(x^2+y^2)$
- Argument of $z,\mathrm{Arg}(z)$, is the angle between the line joining $z$ to the origin and the positive real direction and lies in the interval $(-\pi .\pi )$

Summary

The polar form of complex numbers is particularly useful in multiplying and dividing complex numbers, simplifying computations by converting multiplication to addition of angles and division to subtraction of angles. The polar form also extends to Euler's formula, bridging complex analysis and trigonometry. Understanding the polar form of complex numbers provides powerful tools for performing complex arithmetic and analyzing various physical and engineering systems.

Solved Examples Based on Polar Form of a Complex Number

Example 1: If z is a non-real complex number, then the minimum value of $\frac{\mathrm{Im}{z}^5}{(\mathrm{Im}z{)}^3}$.

Solution:

As we have learned

Polar Form of a Complex Number -

$z=r(\cos \theta +i\sin \theta )$

- wherein

$\mathrm{z}=$ modulus of z and $\theta$ is the argument of Z

Euler's Form of a Complex Number -

$z=r{e}^{i\theta }$

- wherein

r denotes the modulus of z and $\theta$ denotes the argument of z.

$z=x+iy=r(\cos \theta +i\sin \theta )$

$=r{e}^{i\theta }$

So, $\mathrm{Im}{z}^5=\mathrm{Im}{\left(r{e}^{i\theta }\right)}^5$

$=\mathrm{Im}\left(r^5{e}^{i\theta 5}\right)$

$=r^5\sin 50$

$(\mathrm{Im}z{)}^5=(r\sin \theta {)}^5$

$=(r^5{\sin }^5\theta )$

So, $\frac{\mathrm{Im}{z}^5}{(\mathrm{Im}z{)}^5}=\frac{\sin 5\theta }{{\sin }^5\theta }$

for minimum value, differentiating w.r.t $\theta$

So, $\frac{{\sin }^5\theta \cdot 5\cos \theta -5\sin 5\theta {\sin }^4\theta \cos \theta }{{\sin }^{10}\theta }$

$\Rightarrow \sin \theta \cdot \cos 5\theta -\sin 5\theta \cos \theta =0$

$\begin{array}{rl}& \Rightarrow \sin 4\theta \cdot =0\\ & 4\theta =n\pi \\ & \theta =n\pi /4\end{array}$

for $\mathrm{n}=1$

$\frac{\sin 5\theta }{{\sin }^5\theta }=\frac{-1/\sqrt{2}}{(1/\sqrt{2}{)}^5}=-4$

Hence, the answer is -4.

Example 2: If z is a complex number of unit modulus and argument $\theta$ ,then arg $\left(\frac{1+z}{1+\overline{z}}\right)$ equals:

Solution:

$|z|=1$

$\mathrm{Arg}(z)=\theta$

So, $\frac{1+z}{1+\overline{z}}=\frac{1+\cos \theta +i\sin \theta }{1+\cos \theta -i\sin \theta }$

$\frac{2{\cos }^2\theta /2+2i\sin \theta /2\cos \theta /2}{2{\cos }^2\theta /2-2i\sin \theta /2\cos \theta /2}$

$=\frac{\cos \theta /2+i\sin \theta /2}{\cos \theta /2-i\sin \theta /2}$

$=\frac{e^{i\theta /2}}{e^{-i\theta /2}}$

$=e^{i\theta }$

Thus, arg$\left(\frac{1+z}{1+\overline{z}}\right)=\theta$

Hence, the answer is $\theta$.

Example 3: Let $z_1$ and $z_2$ be any two non-zero complex numbers such that $3\left|z_1\right|=2\left|z_2\right|$. If $z=\frac{3z_1}{2z_2}+\frac{2z_2}{3z_1}$ then :

1) $\mathrm{Re}(\mathrm{z})=0$
2) $=1=\sqrt{5/2}$
3) $|z|=\frac{1}{2}\sqrt{34}$
4) $\ln (z)=0$

Solution:

If $z=\frac{3z1}{222}+\frac{2\pi 2}{32}$
Given, ${}^3\left|Z_1\right|=2\mid Z_2$
$\Rightarrow \frac{\left|3Z_1\right|}{\left|2Z_2\right|}=\left|\frac{3Z_1}{2Z_2}\right|=1$
$\mathrm{Let}\frac{3-1}{2z2}=a=\cos \theta +i\sin \theta$

$\begin{array}{rl}& z=a+\frac{1}{a}\\ & z=\cos \theta +i\sin \theta +\frac{1}{\cos \theta +i\sin \theta }\\ & z=\cos \theta +i\sin \theta +\frac{1}{\cos \theta +i\sin \theta }\times \frac{\cos \theta -i\sin \theta }{\cos \theta -i\sin \theta }\\ & z=\cos \theta +i\sin \theta +\frac{\cos \theta -i\sin \theta }{{\cos }^2\theta -i^2{\sin }^2\theta }(i^2=-1)\end{array}$

$\begin{array}{rl}& z=\cos \theta +i\sin \theta +\frac{\cos \theta -i\sin \theta }{1}\\ & z=2\cos \theta +0i\\ & \mathrm{Im}(z)=0\end{array}$

Hence, the answer is the option 4.

Example 4: If $z$ and $w$ are two complex numbers such that $|zw|=1$ and $\arg (z)-\arg (w)=\frac{\pi }{2}$ then :

1) $z\overline{w}=i$

2) $z\overline{w}=\frac{-1+i}{\sqrt{2}}$

3) $\overline{z}w=-i$

4) $z\overline{w}=\frac{1-i}{\sqrt{2}}$

Solution:

Euler's Form of a Complex Number -

$z=r{e}^{ig}$

- wherein

r denotes the modulus of z and $\theta$ denotes the argument of z.

Polar Form of a Complex Number -

$z=r(\cos \theta +i\sin \theta )$

- wherein

r= modulus of z and $\theta$ is the argument of z

Now,

$|zw|=1_{\text{and }}\arg (z)-\arg (w)=\frac{\pi }{2}$

Let $|z|=r$ $=>z=r{e}^{i\theta }$

$|\omega |=\frac{1}{r}$ $=>\omega =\frac{1}{r}{e}^{i\varphi }$

$\arg (z)-\arg (w)=\frac{\pi }{2}$

$\theta -\varphi =\frac{\pi }{2}$

$\theta =\frac{\pi }{2}+\varphi$

$z\overline{\omega }=r{e}^{i\theta }\cdot \frac{1}{r}{e}^{-i\varphi }$

$=r{e}^{i(\theta -\varphi )}$

$=r{e}^{i(\frac{\pi }{2}+\varphi -\varphi )}$

$\equiv r{e}^{i\left(\frac{\pi }{2}\right)}$

$=\cos \left(\frac{\pi }{2}\right)+i\sin \left(\frac{\pi }{2}\right)$

$=0+i.1$

$=i$

Hence, the answer is the option (1).

Example 5: Polar form of $z=\frac{1+7i}{(2-i{)}^2}$ will be :

Solution:

As we learned in

Polar Form of a Complex Number

$z=r(\cos \theta +i\sin \theta )$

where r is the modulus of z and $\theta$ is the argument of z

Now,

$z=\frac{1+7i}{(2-i{)}^2}=\frac{1+7i}{3-4i}\times \frac{3+4i}{3+4i}=\frac{-25+25i}{25}$

$\Rightarrow z=-1+i$

$r=|z|=\sqrt{2}$ and $\arg (z)=\pi -{\tan }^{-1}\frac{1}{-1}$

$\begin{array}{rl}& \Rightarrow r=\sqrt{2}\text{ and }\arg (z)=\pi -\frac{\pi }{4}=\frac{3\pi }{4}\\ & \therefore z=\sqrt{2}(\cos \frac{3\pi }{4}+i\sin \frac{3\pi }{4})\end{array}$

Hence, the answer is $\sqrt{2}(\cos \frac{3\pi }{4}+i\sin \frac{3\pi }{4})$.