Quadratic Equation - Definition, Formula and How to Solve

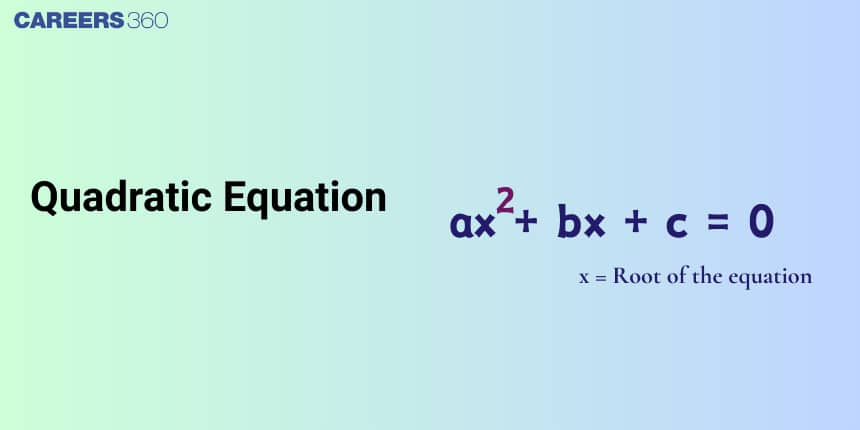
Polynomial Expression – Definition and Basics

An expression of the form

$f(x) = a_0x^n + a_1x^{n-1} + a_2x^{n-2} + \ldots + a_{n-1}x + a_n$

is called a polynomial expression, where $x$ is a variable and $a_0, a_1, a_2, \ldots, a_n$ are constants known as coefficients. Here, $a_0 \neq 0$ and $n$ is a non-negative integer.

Degree of a Polynomial

The degree of a polynomial is the highest power of the variable in the expression.

For example, in $a_0x^n + a_1x^{n-1} + \ldots + a_n$, the highest power of $x$ is $n$, so the degree is $n$.

• If the coefficients are real numbers, it is called a real polynomial.

• If the coefficients are complex numbers, it is called a complex polynomial.

Roots of a Polynomial

If $f(x)$ is a polynomial, then the equation $f(x) = 0$ is called a polynomial equation.

• The value of $x$ that satisfies $f(x) = 0$ is called a root of the polynomial equation.

• If $x = \alpha$ is a root, then $f(\alpha) = 0$.

Example: $x=2$ is a root of $x^2 - 3x + 2 = 0$, because substituting $x=2$ satisfies the equation.

A polynomial equation of degree $n$ has exactly $n$ roots (real or imaginary).

Quadratic Equation – Definition and Standard Form

A quadratic equation is a polynomial equation in which the highest degree of the variable is $2$.

The standard form of a quadratic equation is:

$ax^2 + bx + c = 0$

where $a, b,$ and $c$ are constants (real or complex), and $a \neq 0$. Here, $a$ is called the leading coefficient.

Examples of Quadratic Equations

$-5x^2 - 3x + 2 = 0,\quad x^2 = 0,\quad (1+i)x^2 - 3x + 2i = 0$

Since the degree of a quadratic polynomial is $2$, every quadratic equation has exactly 2 roots (real or complex).

Roots of Quadratic Equation – Quadratic Formula

The roots of a quadratic equation are given by the quadratic formula:

$x = \frac{-b \pm \sqrt{D}}{2a}$ where $D$ is the discriminant, defined as $D = b^2 - 4ac$.

Derivation of the Quadratic Formula

Starting with the general quadratic equation:

$ax^2 + bx + c = 0$

Divide through by $a$:

$x^2 + \frac{b}{a}x + \frac{c}{a} = 0$

Complete the square:

$\left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2}$

Take the square root:

$x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a}$

So,

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

This formula works for all quadratic equations, regardless of the values of $a, b, c$.

Discriminant of a Quadratic Equation

The discriminant of a quadratic equation is the term $D = b^2 - 4ac$ in the quadratic formula. It determines the Nature of Roots of Quadratic Equations:

• If $D > 0$ → two distinct real roots.

• If $D = 0$ → two equal real roots.

• If $D < 0$ → two complex conjugate roots.

Example:
For $x^2 - 4x + 3 = 0$,

$D = (-4)^2 - 4 \cdot 1 \cdot 3 = 16 - 12 = 4 > 0$

So the equation has two distinct real roots.

Sum and Product of Roots of a Quadratic Equation

If $\alpha$ and $\beta$ are the roots of a quadratic equation $ax^2 + bx + c = 0$, then the relationships between the coefficients and the roots can be derived from the quadratic formula.

Sum of Roots

The sum of the roots is defined as:

$\alpha + \beta = \frac{-b}{a}$

Derivation:
Using the quadratic formula:

$\alpha = \frac{-b + \sqrt{D}}{2a}, \quad \beta = \frac{-b - \sqrt{D}}{2a}$

Adding these two roots:

$\alpha + \beta = \frac{-b + \sqrt{D}}{2a} + \frac{-b - \sqrt{D}}{2a} = \frac{-2b}{2a} = \frac{-b}{a}$

Interpretation:
The sum of roots depends only on the coefficients $a$ and $b$. It is independent of $c$ or the nature of the roots.

Example: For $x^2 - 5x + 6 = 0$, $a = 1, b = -5$.
Sum of roots: $\alpha + \beta = \frac{-(-5)}{1} = 5$

Product of Roots

The product of the roots is defined as:

$\alpha \cdot \beta = \frac{c}{a}$

Derivation:
Using the quadratic formula:

$\alpha \cdot \beta = \left(\frac{-b + \sqrt{D}}{2a}\right) \cdot \left(\frac{-b - \sqrt{D}}{2a}\right)$

$= \frac{(-b)^2 - (\sqrt{D})^2}{4a^2} = \frac{b^2 - D}{4a^2}$

Since $D = b^2 - 4ac$,

$\alpha \cdot \beta = \frac{b^2 - (b^2 - 4ac)}{4a^2} = \frac{4ac}{4a^2} = \frac{c}{a}$

Example: For $x^2 - 5x + 6 = 0$, $a = 1, c = 6$
Product of roots: $\alpha \cdot \beta = \frac{6}{1} = 6$

Difference of Roots

The difference of the roots is defined as:

$\alpha - \beta = \left|\frac{\sqrt{D}}{a}\right|$

Derivation:
From the quadratic formula:

$\alpha - \beta = \frac{-b + \sqrt{D}}{2a} - \frac{-b - \sqrt{D}}{2a} = \frac{2\sqrt{D}}{2a} = \frac{\sqrt{D}}{a}$

Remark:

• If $D > 0$, the roots are real and distinct, so $\alpha - \beta$ is positive.

• If $D = 0$, the roots are equal, so $\alpha - \beta = 0$.

• If $D < 0$, the roots are complex conjugates, and the difference is purely imaginary.

Forming a Quadratic Equation from Its Roots

Knowing the sum and product of roots, a quadratic equation can be formed using:

$x^2 - (\alpha + \beta)x + (\alpha \cdot \beta) = 0$

Example 1: If the roots are $2$ and $3$,

Sum = $2 + 3 = 5$, Product = $2 \cdot 3 = 6$

Quadratic equation: $x^2 - 5x + 6 = 0$

Example 2 (Complex Roots): If the roots are $1 + i$ and $1 - i$,

Sum = $(1+i) + (1-i) = 2$, Product = $(1+i)(1-i) = 1^2 - i^2 = 2$

Quadratic equation: $x^2 - 2x + 2 = 0$

Examples of Quadratic Equations with Roots

Example 1: Solve $x^2 - 5x + 6 = 0$

$D = (-5)^2 - 4 \cdot 1 \cdot 6 = 25 - 24 = 1$

$x = \frac{-(-5) \pm \sqrt{1}}{2 \cdot 1} = \frac{5 \pm 1}{2}$

So, $x = 3, 2$

Example 2: Solve $x^2 + 2x + 5 = 0$

$D = 2^2 - 4 \cdot 1 \cdot 5 = 4 - 20 = -16 < 0$

$x = \frac{-2 \pm \sqrt{-16}}{2 \cdot 1} = \frac{-2 \pm 4i}{2} = -1 \pm 2i$

Solved Examples Based on the Quadratic Equations

Example 1: If $a, b, c, d \in \mathbb{R}$ there are two equations $ax^2 + bx + c = 0$, $ax^2 + dx - c = 0$ such that $a \ne 0$ then

1. Both equations will have real roots

2. Both equations will have imaginary roots

3. One will have real roots and other will have imaginary roots

4. At least one will have real roots

Solution:

System of quadratic equations. -

If $ax^2 + bx + c = 0$ and $px^2 + qx + r = 0$ have discriminants $D_1$ and $D_2$ such $D_1 + D_2 \geq 0$ then at least one quadratic has real roots $(a, b, c, p, q, r \in \mathbb{R})$

$D_1 = b^2 - 4ac$

$D_2 = d^2 + 4ac$

$D_1 + D_2 = b^2 + d^2 \geq 0$

This is possible when at least one of $D_1$ & $D_2$ is nonnegative, So at least one will have real roots.

Hence, the answer is the option (4).

Example 2: If $p, q, r, s \in \mathbb{R}$ then the equation $(x^2 + px + s)(x^2 + qx + s)(x^2 + rx - 2s) = 0$ have:

1. two real roots

2. 4 real roots

3. six real roots

4. (correct) at least two real roots

Solution:

System of quadratic equations. -

If $ax^2 + bx + c = 0$ and $px^2 + qx + r = 0$ have discriminants $D_1$ and $D_2$ such $D_1 + D_2 \geq 0$ then at least one quadratic has real roots $(a, b, c, p, q, r \in \mathbb{R})$

$D_1 = p^2 - 4s$; $D_2 = q^2 - 4s$; $D_3 = r^2 + 8s$

$D_1 + D_2 + D_3 = p^2 + q^2 + r^2 \geq 0$

$\implies$ at least one of $D_1, D_2$, $D_3$ is non-negative so at least one factor will have real roots, so at least two real roots are there.

Hence, the answer is the option (4).

Example 3: If $\alpha$ is a root of $4x^2 + 2x - 1 = 0$ then $4\alpha^3 - 2\alpha + \frac{1}{2}$ equals:

1. 0

2. 1

3. 2

4. 3

Solution:

Degree reduction -

If $\alpha$ is a root of $ax^2 + bx + c = 0$ then
$aa^2 + b\alpha + c = 0 \implies a\alpha^2 = -b\alpha - c$ which can be used to reduce degree of $\alpha$ from $2$ to $1$.

$\therefore$ $\alpha$ is a root of $4x^2 + 2x - 1 = 0$

$\Rightarrow 4\alpha^2 = 1 - 2\alpha$

$\therefore \ 4\alpha^3 - 2\alpha + \frac{1}{2} = \alpha \left( 4\alpha^2 \right) - 2\alpha + \frac{1}{2}$

$= \alpha (1 - 2\alpha) - 2\alpha + \frac{1}{2}$

$= -2\alpha^2 - \alpha + \frac{1}{2}$

$= -2 \left( \frac{1 - 2\alpha}{4} \right) - \alpha + \frac{1}{2}$

$= \frac{-(1 - 2\alpha) - 2\alpha + 2}{2} = 0$

Hence, the answer is the option (1).

Example 4: Which of the following is quadratic expression for all $a \in \mathbb{R}$

1. $(a^2 - 1)x^2 + ax + 1$

2. $(a^2 + 1)x^2 + x + 3$

3. $(a + 2)x^2 + x - 3$

4. $(2a - 1)x^2 - x + 5a$

Solution:

Quadratic Expression

$f(x) = ax^2 + bx + c$, where $a \ne 0$

Now, In option (A), for $a = 1, -1$, coefficient of $x^2$ becomes $0$, so it is not a quadratic equation for all real values of $a$.

In option (C), for $a = -2$, coefficient of $x^2$ becomes $0$, so it is not a quadratic equation for all real values of $a$.

In option (D), for $a = 1/2$, coefficient of $x^2$ becomes $0$, so it is not a quadratic equation for all real values of $a$.

But in option (B), the coefficient of $x^2$ will be never zero for any real value of $a$, so (B) will represent a quadratic equation for all $a \in \mathbb{R}$.

Hence, the answer is the option 2.

Example 5: Value of '$a$' for which $(a^2 - 1)x^2 + (2a + 3)x + 5 = 0$ represents a quadratic equation with real coefficients is

1. $\pm 1$

2. $\mathbb{R} - {+1, -1}$

3. $\mathbb{R}$

4. $\mathbb{R}^+$

Solution:

Quadratic Equation with real Coefficients -

An equation of the form $ax^2 + bx + c = 0$ wherein

$a, b, c \in \mathbb{R}$ and $a \ne 0$

for quadratic equation $a^2 - 1 \ne 0$

$a^2 \ne 1$

so $a \ne 1, -1$

Hence, the answer is the option 2.

List of Topics related to Quadratic Equations

Explore a comprehensive list of topics related to quadratic equations, including real-life applications for Class 10 and Class 12 students.

NCERT Resources

Access the best NCERT resources for quadratic equations, including detailed notes, step-by-step solutions, and exemplar problems to strengthen your understanding and practice for board exams and competitive tests.

• NCERT Maths Notes for Class 11th Chapter 4 - Complex Numbers and Quadratic Equations

• NCERT Maths Solutions for Class 11th Chapter 4 - Complex Numbers and Quadratic Equations

• NCERT Maths Exemplar Solutions for Class 11th Chapter 4 - Complex Numbers and Quadratic Equations

Practice Questions based on Quadratic Equations

Solve a variety of practice questions based on quadratic equations, ranging from simple exercises to challenging problems, to master concepts like roots, factorization, discriminant, and real-world applications.

Quadratic Equation - Practice Question MCQ

We have shared below the links to the practice questions sets on the related topics: